《2025年课时训练七年级数学下册苏科版江苏人民出版社》

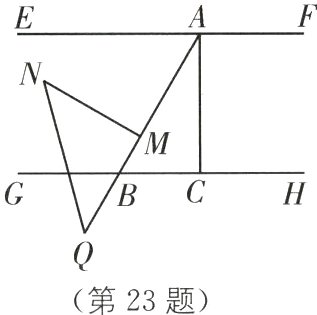
23. （8分）（2024·无锡宜兴期中）如图，EF//GH，点A在EF上，点B，C在GH上. 在△ABC中，∠ACB=90°，∠BAC=30°. 点M，Q在直线AB上，在△MNQ中，∠NMQ=90°，∠MNQ=45°.
（1）将△MNQ沿直线AB平移，当点N在EF上时，请画出图形并求∠ANQ的度数；
（2）将△MNQ沿直线AB平移，当以A，Q，N为顶点的三角形中，有两个角相等时，请画出示意图并直接写出∠QAN的度数.
解：（1）∴∠ANQ=30° + 45° = 75°.
（2）∠QAN的度数为22.5°，45°，67.5°或90°.

答案：

(1)图
(1)即为所求。
∵∠ACB=90°，∠BAC=30°，
∴∠ABC=60°。
∵EF//GH，
∴∠NAM=∠ABC=60°，

∵∠NMQ=90°，
即∠AMN=90°，
∴∠ANM=30°。
∵∠MNQ=45°，
∴∠ANQ=30°+45°=75°。
(2)①当∠ANQ=∠AQN时，如图
(2)，
此时∠AQN=∠ANQ=∠MNQ=45°，
∴∠NAQ=90°。
②当∠QAN=∠AQN时，如图
(3)。
∵∠NMQ=90°，∠MNQ=45°，
∴∠MQN=45°，
∴∠QAN=∠AQN=45°。

③当∠ANQ=∠QAN时，如图
(4)。
∵∠NNQ=90°，∠MNQ=45°，
∴∠NQA=45°，
∴∠QAN=∠ANQ=$\frac{1}{2}$(180°−∠NQA)=67.5°。
④当∠QNA=∠QAN时，如图
(5)。


(第23题)
∵∠NMQ=90°，∠MNQ=45°，
∴∠MQN=45°，
∴∠AQN=180°−∠MQN=135°。
∵∠QNA=∠QAN，
∴∠QAN=$\frac{1}{2}$(180°−∠AQN)=22.5°。
综上，∠QAN的度数为22.5°，45°，67.5°或90°。

24. （8分）（2023·江苏扬州邗江区期末）如果两个角之差的绝对值等于45°，则称这两个角互为“半余角”，即若|∠α - ∠β| = 45°，则称∠α，∠β互为半余角.（注：本题中的角是指大于0°且小于180°的角）
（1）若∠A=80°，则∠A的半余角的度数为 ；
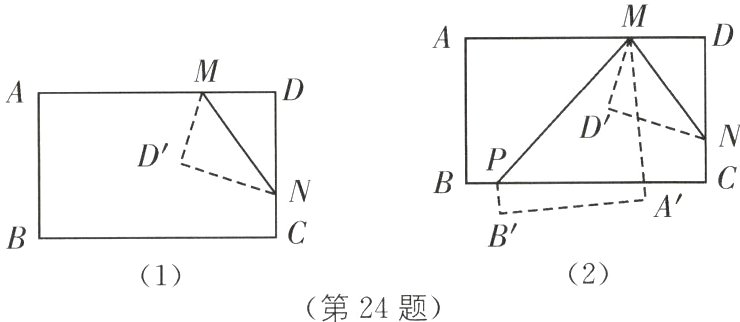
（2）如图（1），将长方形纸片ABCD沿MN折叠（点M，N分别在线段AD，CD上），使点D落在点D′处，若∠AMD′与∠DMN互为“半余角”，求∠DMN的度数；
（3）如图（2），在（2）的条件下再将纸片沿着PM折叠（点P在线段BC上），点A，B分别落在点A′，B′处，若∠AMP比∠DMN大5°，求∠A′MD′的度数.
解：（2）∠DMN=45°或75°.
（3）∠A′MD′=10°或130°.

答案：
(1)125°或35° [解析]设∠A的半余角的度数为α，根据互为半余角的定义，得|80°−α|=45°，
∴α=125°或α=35°。
(2)由折叠，知∠DMN=∠D'MN。
∵∠AMD'与∠DMN互为"半余角"，
∴|∠AMD'−∠DMN|=45°。
当∠AMD'−∠DMN=45°时，则∠AMD'=45°+∠DMN。
∵∠AMD'+∠D'MN+∠DMN=180°，
∴45°+∠DMN+∠DMN+∠DMN=180°，
∴∠DMN=45°；
当∠DMN−∠AMD'=45°时，
则∠AMD'=∠DMN−45°。
∵∠AMD'+∠D'MN+∠DMN=180°，
∴∠DMN−45°+∠DMN+∠DMN=180°，
∴∠DMN=75°。
综上，∠DMN=45°或75°。
(3)由
(2)知∠DMN=75°或45°，
∵∠AMP比∠DMN大5°，
∴∠AMP=45°+5°=50°或75°+5°=80°，
由折叠知，∠A'MP=∠AMP=50°或80°，
∴∠AMA'=100°或160°。
又∠DMN=75°或45°，
∴∠AMD'=90°或30°，
∴∠A'MD'=10°或130°。