《2025年新课标同步单元练习七年级数学下册北师大版深圳专版》

1. 在学习“轴对称现象”内容时，王老师让同学们寻找身边的轴对称图形，小明有一副三角尺和一个量角器(如图5-1-9所示)．

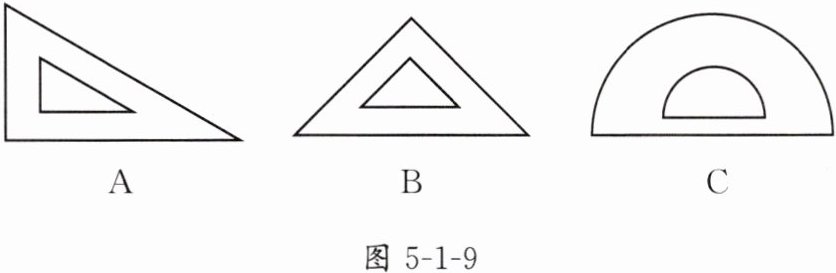
(1)小明的这三件文具中，可以看作是轴对称图形的是__________(填字母代号)；
(2)请用这三件文具中的两件拼成一个轴对称图形，并画出草图(只需画出一种即可)．

答案：
B，C@@如答图5 - 1 - 2（答案不唯一）.

2. 如图5-1-10，将笔记本活页一角折过去，使角的顶点A落在点A′处，BC为折痕．
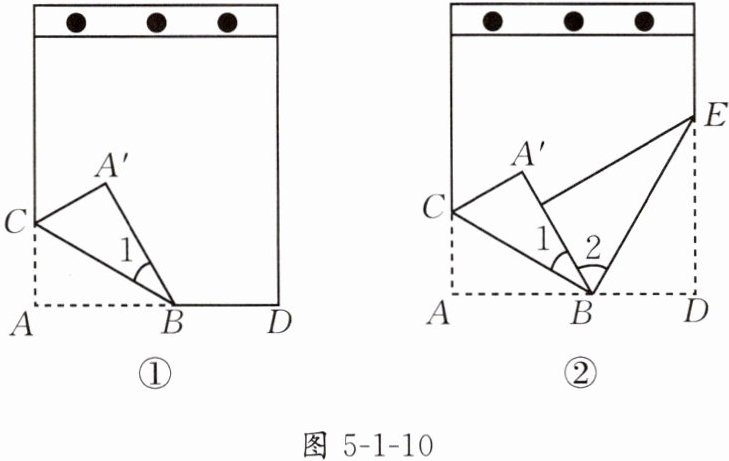
(1)如图5-1-10①，若∠1 = 30°，则∠A′BD的度数是__________．
(2)如果将活页的另一角又斜折过去，使BD与BA′重合，折痕为BE，如图5-1-10②所示，∠1 = 30°，求∠2以及∠CBE的度数．
(3)如果在图5-1-10②中改变∠1的大小，BA′的位置也随之改变，那么问题(2)中∠CBE的大小是否改变? 请说明理由．

答案： 解：（1）120°
（2）因为BD与BA'重合，折痕为BE，所以∠2 = ∠DBE = 1/2∠A'BD = 1/2×120° = 60°，所以∠CBE = ∠1 + ∠2 = 30° + 60° = 90°.
（3）∠CBE的大小不变. 理由：由折叠性质得∠1 = ∠ABC = 1/2∠ABA'，∠2 = ∠DBE = 1/2∠A'BD，所以∠1 + ∠2 = 1/2∠ABA' + 1/2∠A'BD = 1/2（∠ABA' + ∠A'BD） = 1/2×180° = 90°，即∠CBE = 90°.