第106页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
1. 在△ABC中,BD平分∠ABC,CD平分∠ACB,
(1)如图5-2-27①,若∠ABC = 60°,∠ACB = 40°,求∠BDC的度数;
(2)如图5-2-27②,连接AD,过点D作DE⊥AB于点E,DE = 2,AC = 4,求△ADC的面积.
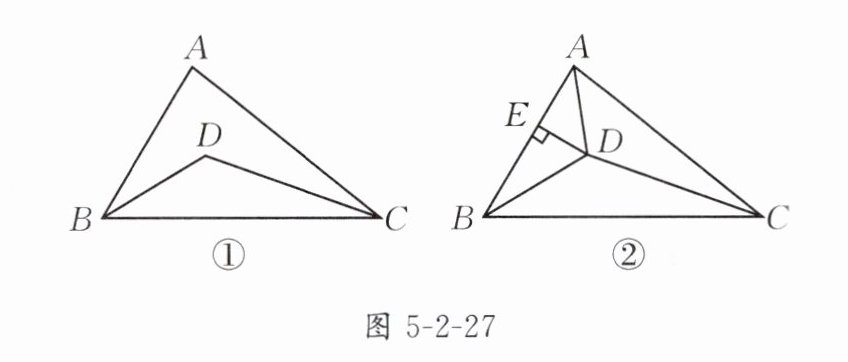
(1)如图5-2-27①,若∠ABC = 60°,∠ACB = 40°,求∠BDC的度数;
(2)如图5-2-27②,连接AD,过点D作DE⊥AB于点E,DE = 2,AC = 4,求△ADC的面积.

答案:
解:(1)因为BD平分∠ABC, 所以∠DBC = 1/2∠ABC = 1/2×60° = 30°. 因为CD平分∠ACB, 所以∠DCB = 1/2∠ACB = 1/2×40° = 20°, 所以∠BDC = 180° - ∠DBC - ∠DCB = 180° - 30° - 20° = 130°.
(2)过点D作DF⊥AC于F,DH⊥BC于H,如答图5 - 2 - 8,
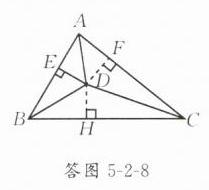
因为BD平分∠ABC,DE⊥AB,DH⊥BC, 所以DH = DE = 2. 因为CD平分∠ACB,DF⊥AC,DH⊥BC, 所以DF = DH = 2, 所以△ADC的面积 = 1/2DF·AC = 1/2×2×4 = 4.
解:(1)因为BD平分∠ABC, 所以∠DBC = 1/2∠ABC = 1/2×60° = 30°. 因为CD平分∠ACB, 所以∠DCB = 1/2∠ACB = 1/2×40° = 20°, 所以∠BDC = 180° - ∠DBC - ∠DCB = 180° - 30° - 20° = 130°.
(2)过点D作DF⊥AC于F,DH⊥BC于H,如答图5 - 2 - 8,

因为BD平分∠ABC,DE⊥AB,DH⊥BC, 所以DH = DE = 2. 因为CD平分∠ACB,DF⊥AC,DH⊥BC, 所以DF = DH = 2, 所以△ADC的面积 = 1/2DF·AC = 1/2×2×4 = 4.
2. 如图5-2-28①,在△ABC中,若AD是∠BAC的平分线,过点D分别作DE⊥AB,DF⊥AC,垂足分别为E,F,则DE = DF.
探究发现:如图5-2-28②,在△ABC中,仍然有条件“AD是∠BAC的平分线,点E,F分别在AB和AC上”.若∠AED + ∠AFD = 180°,则DE与DF是否仍相等?若相等,请说明理由;若不相等,请举反例说明.
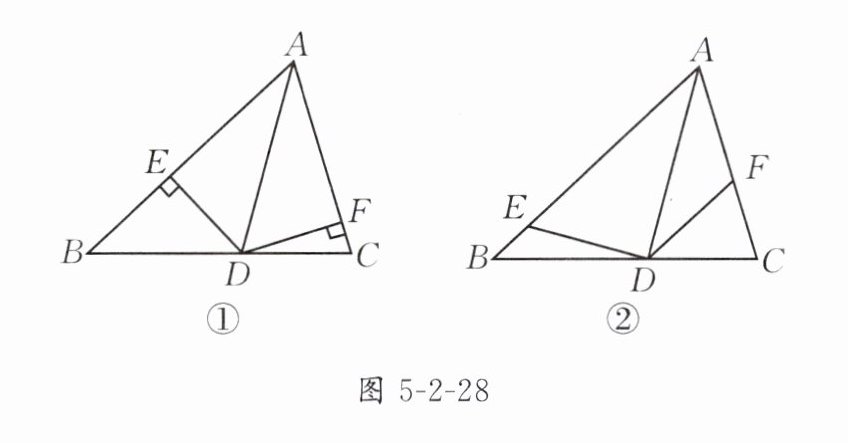
探究发现:如图5-2-28②,在△ABC中,仍然有条件“AD是∠BAC的平分线,点E,F分别在AB和AC上”.若∠AED + ∠AFD = 180°,则DE与DF是否仍相等?若相等,请说明理由;若不相等,请举反例说明.

答案:
解:DE = DF. 理由如下: 如答图5 - 2 - 9,过点D作DM⊥AB于M,DN⊥AC于N,
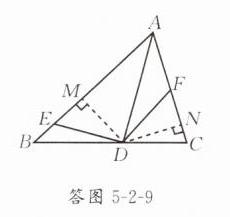
因为AD平分∠BAC,DM⊥AB,DN⊥AC, 所以DM = DN. 因为∠AED + ∠AFD = 180°,∠AFD + ∠DFN = 180°, 所以∠DFN = ∠AED. 在△DME与△DNF中,

所以△DME≌△DNF(AAS). 所以DE = DF.
解:DE = DF. 理由如下: 如答图5 - 2 - 9,过点D作DM⊥AB于M,DN⊥AC于N,

因为AD平分∠BAC,DM⊥AB,DN⊥AC, 所以DM = DN. 因为∠AED + ∠AFD = 180°,∠AFD + ∠DFN = 180°, 所以∠DFN = ∠AED. 在△DME与△DNF中,

所以△DME≌△DNF(AAS). 所以DE = DF.
3. 角平分线上的点到角两边的距离相等.这一性质在解决图形面积问题时有何妙用呢?阅读材料:如图5-2-29①,在面积为S的△ABC中,BC = a,AC = b,AB = c,三条角平分线的交点O到三边的距离为r.连接OA,OB,OC,△ABC被划分为三个小三角形.
因为$S = S_{△OBC}+ S_{△OAC}+ S_{△OAB}$=$\frac{1}{2}$BC·r + $\frac{1}{2}$AC·r + $\frac{1}{2}$AB·r = $\frac{1}{2}$(a + b + c)·r,所以r = $\frac{2S}{a + b + c}$.
(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图5-2-29②,各边长分别为AB = a,BC = b,CD = c,AD = d,求点O到四边的距离r(用含S,a,b,c,d的代数式表示);
(2)理解应用:如图5-2-29③,在四边形ABCD中,AB//DC,AB = 21,CD = 11,AD = BC = 13,对角线BD = 20,点$O_{1}$与$O_{2}$分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为$r_{1}$和$r_{2}$,求$\frac{r_{1}}{r_{2}}$的值.

因为$S = S_{△OBC}+ S_{△OAC}+ S_{△OAB}$=$\frac{1}{2}$BC·r + $\frac{1}{2}$AC·r + $\frac{1}{2}$AB·r = $\frac{1}{2}$(a + b + c)·r,所以r = $\frac{2S}{a + b + c}$.
(1)类比推理:若面积为S的四边形ABCD的四条角平分线交于O点,如图5-2-29②,各边长分别为AB = a,BC = b,CD = c,AD = d,求点O到四边的距离r(用含S,a,b,c,d的代数式表示);
(2)理解应用:如图5-2-29③,在四边形ABCD中,AB//DC,AB = 21,CD = 11,AD = BC = 13,对角线BD = 20,点$O_{1}$与$O_{2}$分别为△ABD与△BCD的三条角平分线的交点,设它们到各自三角形三边的距离为$r_{1}$和$r_{2}$,求$\frac{r_{1}}{r_{2}}$的值.

答案:
解:(1)连接OA,OB,OC,OD(画图略),
因为$S = S_{△AOB} + S_{△BOC} + S_{△COD} + S_{△AOD} = 1/2ar + 1/2br + 1/2cr + 1/2dr = 1/2(a + b + c + d)r,
所以r = 2S/(a + b + c + d).
(2)因为AB//CD,
所以$$S_{△ABD} : S_{△BCD}$ = $AB : CD$ = $21 : 11$$.
因为$$r_{1}$ = $2S_{△ABD}/(AB + BD + AD)$ = $2S_{△ABD}/54$ = $S_{△ABD}/27$$, $$r_{2}$ = $2S_{△CDB}/(CD + CB + DB)$ = $2S_{△CDB}/44$ = $S_{△CDB}/22$$,
所以$$r_{1}/r_{2}$ = $S_{△ABD}/27 : S_{△BCD}/22$ = $S_{△ABD}/27×22/S_{△BCD}$ = $21×22/(27×11)$ = $14/9$.
查看更多完整答案,请扫码查看


