第32页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
4. 解决问题。(主要对应目标:5303、5305、5307、5308、5309)
(1) (广东阳江) 美术课上,老师让同学们探究手中“变废为宝”的作品与数学之间的联系,小轩的作品是一个废弃纸皮制作的长方体抽纸盒,上面有一个长12 cm、宽5 cm的长方形开口(如图)。
① 制作这个抽纸盒至少需要纸皮多少平方厘米?(接口处忽略不计)
列式计算:______________________________
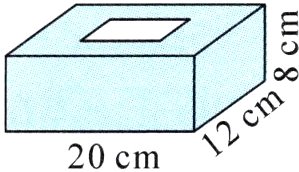
② 这个抽纸盒的占地面积是多少平方厘米?
列式计算:______________________________
③ 这个抽纸盒的体积是多少立方厘米?
列式计算:______________________________
(2) 农历十二月初八是腊八节,我国部分地区有腊八节腌制腊八蒜的习俗。在腊八节这天,妈妈准备教贝贝泡腊八蒜。她们准备了甲、乙两个长方体容器、一把直尺、一些蒜瓣和一些醋。甲长方体容器从里面量长10 cm,宽6 cm,高20 cm,乙长方体容器从里面量长10 cm,宽10 cm,高15 cm。
① 先在甲长方体容器中倒入高6 cm的醋,再将蒜瓣放入甲长方体容器(完全浸没,醋没有溢出),用直尺量得醋的高度上升到10 cm。求这些蒜瓣的体积。
② 清洗两个长方体容器时,先往甲长方体容器中倒满水,再把甲长方体容器中的水全部倒入乙长方体容器,这时乙长方体容器的水深多少厘米?
(3) 手工课上,萌明制作了一个高20 cm,底面是正方形的长方体收纳盒,现在准备把高降低5 cm,那么表面积就减少了160 cm²。求原来长方体收纳盒的表面积和体积。
(1) (广东阳江) 美术课上,老师让同学们探究手中“变废为宝”的作品与数学之间的联系,小轩的作品是一个废弃纸皮制作的长方体抽纸盒,上面有一个长12 cm、宽5 cm的长方形开口(如图)。
① 制作这个抽纸盒至少需要纸皮多少平方厘米?(接口处忽略不计)
列式计算:______________________________

② 这个抽纸盒的占地面积是多少平方厘米?
列式计算:______________________________
③ 这个抽纸盒的体积是多少立方厘米?
列式计算:______________________________
(2) 农历十二月初八是腊八节,我国部分地区有腊八节腌制腊八蒜的习俗。在腊八节这天,妈妈准备教贝贝泡腊八蒜。她们准备了甲、乙两个长方体容器、一把直尺、一些蒜瓣和一些醋。甲长方体容器从里面量长10 cm,宽6 cm,高20 cm,乙长方体容器从里面量长10 cm,宽10 cm,高15 cm。
① 先在甲长方体容器中倒入高6 cm的醋,再将蒜瓣放入甲长方体容器(完全浸没,醋没有溢出),用直尺量得醋的高度上升到10 cm。求这些蒜瓣的体积。
② 清洗两个长方体容器时,先往甲长方体容器中倒满水,再把甲长方体容器中的水全部倒入乙长方体容器,这时乙长方体容器的水深多少厘米?
(3) 手工课上,萌明制作了一个高20 cm,底面是正方形的长方体收纳盒,现在准备把高降低5 cm,那么表面积就减少了160 cm²。求原来长方体收纳盒的表面积和体积。
答案:
(1)①$(20×12 + 20×8 + 12×8)×2 - 12×5 = 932(cm^{2})$ ②$20×12 = 240(cm^{2})$ ③$20×12×8 = 1920(cm^{3})$
(2)①$10×6×(10 - 6)=240(cm^{3})$ ②$10×6×20÷(10×10)=12(cm)$
(3)$160÷4÷5 = 8(cm)$ 原来长方体收纳盒的长、宽、高分别是8 cm、8 cm、20 cm。 表面积:$(8×8 + 8×20 + 8×20)×2 = 768(cm^{2})$ 体积:$8×8×20 = 1280(cm^{3})$
(1)①$(20×12 + 20×8 + 12×8)×2 - 12×5 = 932(cm^{2})$ ②$20×12 = 240(cm^{2})$ ③$20×12×8 = 1920(cm^{3})$
(2)①$10×6×(10 - 6)=240(cm^{3})$ ②$10×6×20÷(10×10)=12(cm)$
(3)$160÷4÷5 = 8(cm)$ 原来长方体收纳盒的长、宽、高分别是8 cm、8 cm、20 cm。 表面积:$(8×8 + 8×20 + 8×20)×2 = 768(cm^{2})$ 体积:$8×8×20 = 1280(cm^{3})$
查看更多完整答案,请扫码查看


