第90页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
(13) 新情境(天津南开)两只蚂蚁沿不同的路线从点$M$爬到点$N$,甲蚂蚁沿虚线爬,乙蚂蚁沿实线爬。下面四幅图中,两只蚂蚁爬的路线一样长的共有(

A.1
B.2
C.3
D.4
C
)幅。
A.1
B.2
C.3
D.4
答案:
13. C
(14)(湖北武汉)如图所示,分别以点$B$、点$C$为圆心的两个半圆的直径都是2厘米,则阴影部分的周长是多少?(结果保留两位小数)


答案:
14. 连接EB、FC。
线段EF=线段BC=2÷2=1(厘米)
连接GB、GC。
三角形GBC是等边三角形。∠GBC = 60°
弧长GC=$\pi×2×\frac{60^{\circ}}{360^{\circ}}=\frac{1}{3}\pi$(厘米)
弧长CE=$\pi×2×\frac{1}{4}=\frac{1}{2}\pi$(厘米)
弧长GF=弧长GE=弧长CE - 弧长GC=$\frac{1}{2}\pi-\frac{1}{3}\pi=\frac{1}{6}\pi$(厘米)
阴影部分的周长=线段EF + 弧长GE + 弧长GF=$1+\frac{1}{6}\pi×2\approx2.05$(厘米)

14. 连接EB、FC。
线段EF=线段BC=2÷2=1(厘米)
连接GB、GC。
三角形GBC是等边三角形。∠GBC = 60°
弧长GC=$\pi×2×\frac{60^{\circ}}{360^{\circ}}=\frac{1}{3}\pi$(厘米)
弧长CE=$\pi×2×\frac{1}{4}=\frac{1}{2}\pi$(厘米)
弧长GF=弧长GE=弧长CE - 弧长GC=$\frac{1}{2}\pi-\frac{1}{3}\pi=\frac{1}{6}\pi$(厘米)
阴影部分的周长=线段EF + 弧长GE + 弧长GF=$1+\frac{1}{6}\pi×2\approx2.05$(厘米)

(15)(湖南长沙)如下图,三角形$ABC$是等腰直角三角形,点$O$是以$AB$边为直径的半圆的圆心,$AD=\frac{1}{2}CD$,$BC = 3BE$,四边形$CDOE$的面积是21平方厘米,阴影部分的面积是多少平方厘米?


答案:
15. 21÷2×(2 + 1)=31.5(平方厘米)
设圆的半径是r厘米。
2r×r÷2 = 31.5
r² = 31.5
2r×r - 3.14×r²÷2=2×31.5 - 3.14×31.5÷2=13.545(平方厘米)
解析:添加辅助线,如下图:
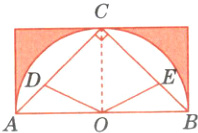
根据AD=$\frac{1}{2}$CD,BC = 3BE可知,DC:AD = 2:1,CE:EB = 2:1。三角形COD与三角形AOD等高,它们的面积比与底边比相等,为2:1。同理,三角形COE与三角形BOE的面积比也是2:1,那么四边形CDOE与三角形BOE、三角形AOD的面积和的比为2:1,三角形ABC的面积是21÷2×(2 + 1)=31.5(平方厘米)。三角形ABC的底为圆的直径,三角形ABC的高为圆的半径,设圆的半径是r厘米,则2r×r÷2 = 31.5,求出r² = 31.5,阴影部分的面积=长方形的面积 - 半圆的面积,据此列式计算即可。
15. 21÷2×(2 + 1)=31.5(平方厘米)
设圆的半径是r厘米。
2r×r÷2 = 31.5
r² = 31.5
2r×r - 3.14×r²÷2=2×31.5 - 3.14×31.5÷2=13.545(平方厘米)
解析:添加辅助线,如下图:

根据AD=$\frac{1}{2}$CD,BC = 3BE可知,DC:AD = 2:1,CE:EB = 2:1。三角形COD与三角形AOD等高,它们的面积比与底边比相等,为2:1。同理,三角形COE与三角形BOE的面积比也是2:1,那么四边形CDOE与三角形BOE、三角形AOD的面积和的比为2:1,三角形ABC的面积是21÷2×(2 + 1)=31.5(平方厘米)。三角形ABC的底为圆的直径,三角形ABC的高为圆的半径,设圆的半径是r厘米,则2r×r÷2 = 31.5,求出r² = 31.5,阴影部分的面积=长方形的面积 - 半圆的面积,据此列式计算即可。
(16)(西安市名校小学毕业考试题)求下图中阴影部分的面积。(单位:厘米)


答案:
16. 等腰直角三角形的面积:10×10÷2=50(平方厘米)
扇形的面积:3.14×10²×$\frac{45^{\circ}}{360^{\circ}}$=39.25(平方厘米)
半圆中空白部分的面积:50 - 39.25=10.75(平方厘米)
图中阴影部分的面积:3.14×(10÷2)²÷2 - 10.75=28.5(平方厘米)
解析:先求出等腰直角三角形的面积,从中减去扇形的面积就是半圆中空白部分的面积。再从半圆的面积中减去空白部分的面积,就是阴影部分的面积。
扇形的面积:3.14×10²×$\frac{45^{\circ}}{360^{\circ}}$=39.25(平方厘米)
半圆中空白部分的面积:50 - 39.25=10.75(平方厘米)
图中阴影部分的面积:3.14×(10÷2)²÷2 - 10.75=28.5(平方厘米)
解析:先求出等腰直角三角形的面积,从中减去扇形的面积就是半圆中空白部分的面积。再从半圆的面积中减去空白部分的面积,就是阴影部分的面积。
(17)(成都市名校新初一入学摸底考试题)如下图,在直角三角形$ABC$中,有一个正方形$ADEF$,已知$CF = 5$厘米,$DB = 16$厘米,求正方形$ADEF$的面积。


答案:
17. 16×5=80(平方厘米)
解析:如图所示,将原图补为一个长方形ABIC,延长FE到H,延长DE到G。
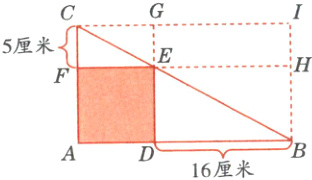
由图可知:在长方形ABIC中,S△ABC = S△ICB,在长方形BDEH中,S△DBE = S△HEB,在长方形CFEG中,S△CFE = S△EGC,所以S△ABC - S△DBE - S△CFE = S△ICB - S△HEB - S△EGC,即正方形ADEF的面积=长方形IHEG的面积=16×5=80(平方厘米)。
17. 16×5=80(平方厘米)
解析:如图所示,将原图补为一个长方形ABIC,延长FE到H,延长DE到G。

由图可知:在长方形ABIC中,S△ABC = S△ICB,在长方形BDEH中,S△DBE = S△HEB,在长方形CFEG中,S△CFE = S△EGC,所以S△ABC - S△DBE - S△CFE = S△ICB - S△HEB - S△EGC,即正方形ADEF的面积=长方形IHEG的面积=16×5=80(平方厘米)。
查看更多完整答案,请扫码查看


