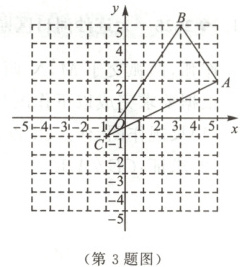
3. 如图,在平面直角坐标系中,$\triangle ABC$的顶点坐标分别为$A(5,2)$,$B(3,5)$,$C(-1,-1)$.
(1)画出$\triangle ABC$关于$y$轴对称的图形$\triangle A_1B_1C_1$.
(2)直接写出点$A_1$,$B_1$,$C_1$的坐标.
(3)求$\triangle A_1B_1C_1$的面积.
(1)画出$\triangle ABC$关于$y$轴对称的图形$\triangle A_1B_1C_1$.
(2)直接写出点$A_1$,$B_1$,$C_1$的坐标.
(3)求$\triangle A_1B_1C_1$的面积.

答案:
3.
(1)如图,△A₁B₁C₁即为所求.

(2)点A₁( - 5,2),B₁( - 3,5),C₁(1, - 1).
(3)解:S△A₁B₁C₁ = $\frac{1}{2}$×(2 + 6)×6 - $\frac{1}{2}$×6×3 - $\frac{1}{2}$×2×3 = 24 - 9 - 3 = 12.
3.
(1)如图,△A₁B₁C₁即为所求.

(2)点A₁( - 5,2),B₁( - 3,5),C₁(1, - 1).
(3)解:S△A₁B₁C₁ = $\frac{1}{2}$×(2 + 6)×6 - $\frac{1}{2}$×6×3 - $\frac{1}{2}$×2×3 = 24 - 9 - 3 = 12.
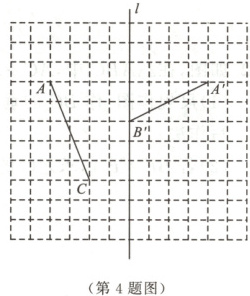
4. 如图,在正方形网格中,直线$l$与网格线重合,点$A$,$C$,$A^\prime$,$B^\prime$均在格点上.
(1)已知$\triangle ABC$和$\triangle A^\prime B^\prime C^\prime$关于直线$l$对称,请在图上把$\triangle ABC$和$\triangle A^\prime B^\prime C^\prime$补充完整.
(2)在以直线$l$为$y$轴的坐标系中,若点$A$的坐标为$(-4,b)$,则点$A^\prime$的坐标为
(3)在直线$l$上找到点$P$,使$PA+PC$最短.
(1)已知$\triangle ABC$和$\triangle A^\prime B^\prime C^\prime$关于直线$l$对称,请在图上把$\triangle ABC$和$\triangle A^\prime B^\prime C^\prime$补充完整.
(2)在以直线$l$为$y$轴的坐标系中,若点$A$的坐标为$(-4,b)$,则点$A^\prime$的坐标为
(4,b)
.(3)在直线$l$上找到点$P$,使$PA+PC$最短.

答案:
4.
(1)如图1,△ABC和△A'B'C'即为所求.

(2)(4,b)
(3)如图2,点P即为所求.

4.
(1)如图1,△ABC和△A'B'C'即为所求.

(2)(4,b)
(3)如图2,点P即为所求.

查看更多完整答案,请扫码查看


