3. 在$Rt\triangle ABC$中,$\angle ACB = 90^{\circ}$,$\angle ABC = 60^{\circ}$,点$D$为射线$AB$上一动点,以$DC$为边作等边三角形$CDE$(点$C$,$D$,$E$按顺时针方向排列),探究线段$EA$与$ED$的数量关系.
(1)如图1,当点$D$与点$B$重合时,点$E$在$AB$上,猜想$EA$与$ED$的数量关系,并说明理由.
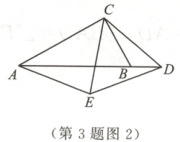
(2)如图2,当点$D$在$AB$的延长线上时,证明(1)中的结论仍然成立.
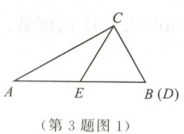
(1)如图1,当点$D$与点$B$重合时,点$E$在$AB$上,猜想$EA$与$ED$的数量关系,并说明理由.
(2)如图2,当点$D$在$AB$的延长线上时,证明(1)中的结论仍然成立.


答案:
3.
(1)解:EA = ED.
理由:
∵△CBE为等边三角形,
∴BC = BE.
∵∠ACB = 90°, ∠ABC = 60°,
∴∠A = 180° - ∠ACB - ∠ABC = 30°.
∴AB = 2BC = 2BE.
∴EA = AB - BE = BE,即EA = ED.
(2)证明:如图,在AB上取点F,使BF = BC,连接CF,EF.
∵BF = BC, ∠ABC = 60°,
∴△CBF为等边三角形.
∴∠FCB = ∠CFB = 60°, BC = FB = FC.
∵△CDE为等边三角形,
∴CE = CD = ED, ∠ECD = 60°.
∴∠ECD - ∠ECB = ∠FCB - ∠ECB,即∠BCD = ∠FCE.
在△CFE和△CBD中,$\begin{cases} CF = CB, \\ ∠FCE = ∠BCD, \\ CE = CD \end{cases}$
∴△CFE≌△CBD(SAS).
∵∠CFE = ∠CBD = 180° - ∠ABC = 120°.
∵∠CFB = 60°,
∴∠EFD = ∠CFE - ∠CFB = 60°.
∴∠AFE = 180° - ∠EFD = 120°.
∴∠AFE = ∠CFE.
由
(1)得,AB = 2BC = 2BF,
∴BF = AF = CF.
在△CFE和△AFE中,$\begin{cases} EF = EF, \\ ∠EFC = ∠EFA, \\ FC = FA \end{cases}$
∴△CFE≌△AFE(SAS).
∴EA = EC = ED.

3.
(1)解:EA = ED.
理由:
∵△CBE为等边三角形,
∴BC = BE.
∵∠ACB = 90°, ∠ABC = 60°,
∴∠A = 180° - ∠ACB - ∠ABC = 30°.
∴AB = 2BC = 2BE.
∴EA = AB - BE = BE,即EA = ED.
(2)证明:如图,在AB上取点F,使BF = BC,连接CF,EF.
∵BF = BC, ∠ABC = 60°,
∴△CBF为等边三角形.
∴∠FCB = ∠CFB = 60°, BC = FB = FC.
∵△CDE为等边三角形,
∴CE = CD = ED, ∠ECD = 60°.
∴∠ECD - ∠ECB = ∠FCB - ∠ECB,即∠BCD = ∠FCE.
在△CFE和△CBD中,$\begin{cases} CF = CB, \\ ∠FCE = ∠BCD, \\ CE = CD \end{cases}$
∴△CFE≌△CBD(SAS).
∵∠CFE = ∠CBD = 180° - ∠ABC = 120°.
∵∠CFB = 60°,
∴∠EFD = ∠CFE - ∠CFB = 60°.
∴∠AFE = 180° - ∠EFD = 120°.
∴∠AFE = ∠CFE.
由
(1)得,AB = 2BC = 2BF,
∴BF = AF = CF.
在△CFE和△AFE中,$\begin{cases} EF = EF, \\ ∠EFC = ∠EFA, \\ FC = FA \end{cases}$
∴△CFE≌△AFE(SAS).
∴EA = EC = ED.

查看更多完整答案,请扫码查看


