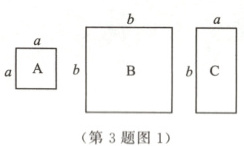
3.数学活动课上,老师准备了如图1所示的三种纸片若干张($A$纸片是边长为$a$的正方形,$B$纸片是边长为$b$的正方形,$C$纸片是长为$b$、宽为$a$的长方形),并用一张$A$纸片、一张$B$纸片和两张$C$纸片拼成如图2所示的大正方形.
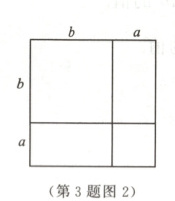
(1)观察图2,直接写出$(a + b)^{2}$,$a^{2}+b^{2}$,$ab$之间的数量关系:
(2)若要拼出一个面积为$(a + 3b)(2a + b)$的长方形,则需要$A$纸片
(3)若$2m + 3n = 10$,$mn = 4$,则$2m - 3n$的值为
(4)根据(1)中的数量关系,解决问题:
已知$(2025 - m)(m - 2023)= - 1010$,求$(2025 - m)^{2}+(m - 2023)^{2}$的值.
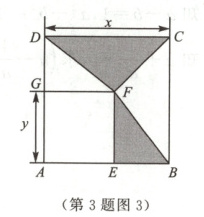
(5)将边长为$x$的正方形$ABCD$和边长为$y$的正方形$AEFG$按如图3所示的方式摆放.若$x^{2}-y^{2}=25$,$BE = 1$,则图中阴影部分的面积之和为



(1)观察图2,直接写出$(a + b)^{2}$,$a^{2}+b^{2}$,$ab$之间的数量关系:
$(a + b)^{2}=a^{2}+b^{2}+2ab$
$.$(2)若要拼出一个面积为$(a + 3b)(2a + b)$的长方形,则需要$A$纸片
2
张,$B$纸片3
张,$C$纸片7
张.(3)若$2m + 3n = 10$,$mn = 4$,则$2m - 3n$的值为
2或 - 2
.(4)根据(1)中的数量关系,解决问题:
已知$(2025 - m)(m - 2023)= - 1010$,求$(2025 - m)^{2}+(m - 2023)^{2}$的值.
(5)将边长为$x$的正方形$ABCD$和边长为$y$的正方形$AEFG$按如图3所示的方式摆放.若$x^{2}-y^{2}=25$,$BE = 1$,则图中阴影部分的面积之和为
$\frac{25}{2}$
.
答案:
3.
(1)$(a + b)^{2}=a^{2}+b^{2}+2ab$
(2)$2\ 3\ 7$
(3)$2$或$-2$
(4)解:设$2025 - m=a,m - 2023=b$,则$a + b=2$,
$ab=-1010$.
$\therefore(2025 - m)^{2}+(m - 2023)^{2}=a^{2}+b^{2}=(a + b)^{2}-$
$2ab=2^{2}-2×(-1010)=2024$.
(5)$\frac{25}{2}$【解析】由题意得,$DG = BE = 1$,
∴$x - y=1$.
∵$x^{2}-y^{2}=25$,
∴$x^{2}-y^{2}=(x + y)(x - y)=25$.
$\therefore x + y=25$.
$\therefore S_{阴影部分}=\frac{1}{2}DC· DG+\frac{1}{2}EF· BE=\frac{1}{2}× x×$
$1+\frac{1}{2}× y×1=\frac{1}{2}(x + y)=\frac{25}{2}$.
(1)$(a + b)^{2}=a^{2}+b^{2}+2ab$
(2)$2\ 3\ 7$
(3)$2$或$-2$
(4)解:设$2025 - m=a,m - 2023=b$,则$a + b=2$,
$ab=-1010$.
$\therefore(2025 - m)^{2}+(m - 2023)^{2}=a^{2}+b^{2}=(a + b)^{2}-$
$2ab=2^{2}-2×(-1010)=2024$.
(5)$\frac{25}{2}$【解析】由题意得,$DG = BE = 1$,
∴$x - y=1$.
∵$x^{2}-y^{2}=25$,
∴$x^{2}-y^{2}=(x + y)(x - y)=25$.
$\therefore x + y=25$.
$\therefore S_{阴影部分}=\frac{1}{2}DC· DG+\frac{1}{2}EF· BE=\frac{1}{2}× x×$
$1+\frac{1}{2}× y×1=\frac{1}{2}(x + y)=\frac{25}{2}$.
查看更多完整答案,请扫码查看


