《2025年点石成金金牌夺冠八年级数学上册人教版辽宁专版》

1. 如图，在$\triangle BDE$和$\triangle BAC$中，$DE = AC$，点$E$在边$AC$上，$DE$与$AB$交于点$F$，$\angle DBF = \angle CBE = \angle AED$. 求证：$\triangle BDE \cong \triangle BAC$.

答案： 1.证明：
∵∠DBF = ∠CBE，
∴∠DBF + ∠FBE = ∠CBE + ∠FBE，
即∠DBE = ∠ABC.
∵∠DBF = ∠AED, ∠DFB = ∠AFE，
∴180° - ∠DBF - ∠DFB = 180° - ∠AED - ∠AFE，
即∠D = ∠A.
在△BDE和△BAC中，$\begin{cases} ∠DBE = ∠ABC, \\ ∠D = ∠A, \\ DE = AC \end{cases}$
∴△BDE≌△BAC(AAS).

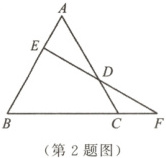
2. 如图，在$\triangle ABC$中，点$D$是边$AC$上一点，$DE \perp AB$于点$E$，延长$ED$交$BC$的延长线于点$F$，$CD = CF$.
(1)求证：$\triangle ABC$是等腰三角形.
(2)当$\angle F =$30°时，$\triangle ABC$是等边三角形. 请填空并给出证明.

答案： 2.
(1)证明：
∵CD = CF，
∴∠CDF = ∠CFD.
∵∠CDF = ∠ADE，
∴∠CFD = ∠ADE.
∵DE⊥AB，
∴∠FEB = ∠DEA = 90°.
∴90° - ∠CFD = 90° - ∠ADE，即∠B = ∠A.
∴CB = CA.
∴△ABC是等腰三角形.
(2)30°
证明：
∵∠F = 30°，
∴∠B = 90° - ∠F = 60°.
∵CB = CA，
∴△ABC是等边三角形.