《2025年拔尖特训六年级数学上册北师大版广东专版》

(1)我国南北朝时期著名的数学家(祖冲之)得到了$\pi$的两个分数形式的近似值：约率为($\frac{22}{7}$)，密率为($\frac{355}{113}$)，并且算出$\pi$的值在$3.1415926$和$3.1415927$之间。

答案： 1.
(1)祖冲之 $\frac{22}{7}$ $\frac{355}{113}$ 

(2)计算圆周率，无论是“穷竭法”，还是“割圆术”，都是逐步逼近的方法，都是(极限)思想的体现，这种思想为微积分的创立奠定了基础。

答案：
(2)极限

(1)我国关于圆周率的记录最早出自(A)。

A.《周髀算经》
B.《九章算术》
C.《孙子算经》
D.《海岛算经》

答案： 2.
(1)A

(2)(深圳福田区)在我国，首先由魏晋时期杰出的数学家(C)得出了较精确的圆周率的值。他采用“割圆术”一直算到圆内接正$192$边形，得到圆周率的近似值是$3.14$，该方法是用圆内接正多边形从一个方向逐步逼近圆。

A.华罗庚
B.杨辉
C.刘徽
D.贾宪

答案： 2.
(2)C

(3)公元前$3$世纪，古希腊数学家(A)用圆内接正多边形和圆外切正多边形从两个方向上逐步逼近圆，获得了圆周率的值介于$\frac{223}{71}$和$\frac{22}{7}$之间。

A.阿基米德
B.柏拉图
C.苏格拉底
D.毕达哥拉斯

答案： 2.
(3)A

3.因为拱形结构具有受力好、外形美观等特点，所以我国古代的城门多为拱形。如图所示为一个拱形城门，其上方是一个半圆，聪聪从城门左侧直行走了$14$步到达城门右侧，他每步大约长$55$厘米。这个半圆的长度是多少米？

答案： 3.14×55=770(厘米)
3.14×770÷2=1208.9(厘米)
1208.9厘米=12.089米

4.公园里有一个半圆形花坛(如图)，它的周长是$20.56$米，则它的半径是多少米？

答案： 4.解：设它的半径是r米。
2×3.14×r÷2+2r=20.56 r=4 检验略

5.实验小学校园里的花坛形状如图所示，中间是一个边长为$8 m$的正方形，四周都是半圆。这个花坛的周长是多少米？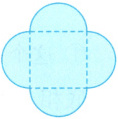

答案： 5.3.14×8×2=50.24(m)

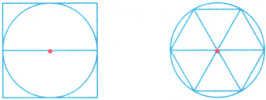
6.(说理表达)请你由圆外切正方形和圆内接正六边形推算出圆周率大于$3$且小于$4$。

答案： 6.从圆外切正方形可以看出正方形的周长是圆直径的4倍，而正方形的周长大于圆的周长，所以圆周率小于4。从圆内接正六边形可以看出正六边形的周长是圆直径的3倍，而圆的周长大于正六边形的周长，所以圆周率大于3。综上所述，圆周率大于3且小于4(合理即可)
解析：观察题图，发现外切正方形与圆、内接正六边形与圆的周长之间的关系，从而解决问题。 讲错