《2025年拔尖特训六年级数学上册北师大版广东专版》

(1) $32:18 = \frac{16}{9}$, 比的前项是(32)，比的后项是(18)，比值是($\frac{16}{9}$)。

答案： 1.
(1)32 18 $\frac{16}{9}$

(2) ★将1克盐溶于50克水中，盐与水的质量比是(1:50)，比值是(0.02)；盐与盐水的质量比是(1:51)，比值是($\frac{1}{51}$)。

答案： 1.
(2)1:50 0.02 1:51 $\frac{1}{51}$
易错分析
区分比和比值的形式
求出的比可以写成“前项:后项”的形式，也可以写成分数的形式(分母是1不能省略)。
比值可以写成分数的形式(分母是1可省略)，也可以写成小数的形式，但不能写成比的形式。

(3) 甲数是乙数的$\frac{2}{3}$，甲、乙两数的比是(2:3)，甲数与两数和的比是(2:5)，乙数与两数差的比是(3:1)。

答案： 1.
(3)2:3 2:5 3:1

2. 判一判。
(1) 比值只能用分数表示。 (×)
(2) 妈妈买了1千克苹果和500克橘子，苹果与橘子的质量比是$1:500$。 (×)
(3) 一场足球比赛的最终比分是$2:0$，说明在特殊情况下，比的后项可以是0。 (×)
(4) 从学校到书店，甲用了6分，乙用了7分，甲和乙的速度比是$6:7$。 (×)

答案： 2.
(1)×
@@2.
(2)×
@@2.
(3)×
@@2.
(4)×

3. 求比值。
$25:80$ $\frac{3}{4}:1.5$ $350米:0.6千米$

答案： 3.$\frac{5}{16}$ $\frac{1}{2}$ $\frac{7}{12}$

4. (生活体验)照片中月月的身高是3厘米，她的实际身高是1.5米。月月照片中的身高与她的实际身高的比是多少?比值呢?

答案： 4.1.5米=150厘米 比:3:150
比值:3:150=$\frac{1}{50}$

5. 有两个长方形，它们的长之比是$3:2$，宽之比是$5:4$，它们的面积之比是多少?

答案： 5.(3×5):(2×4)=15:8
解析:已知两个长方形的长之比和宽之比，要求面积之比，可根据“长方形的面积=长×宽”用(3×5)表示第一个长方形的面积，用(2×4)表示第二个长方形的面积，进而求出两个长方形的面积之比。

6. (生物百科)有关资料研究显示，某种动物的小腿骨与大腿骨的长度的比值越大，这种动物跑得越快。下表是三种动物的小腿骨与大腿骨的长度参考数值。

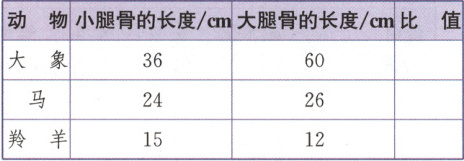
先将表格补充完整，再判断哪种动物跑得最快。

答案： 6.$\frac{3}{5}=\frac{12}{13}＜\frac{5}{4}$ $\frac{3}{5}＜\frac{12}{13}＜\frac{5}{4}$ 羚羊跑得最快

7. (探究创新)左下图中正方形的边长是$8 cm$，右下图中圆的半径是$6 cm$。分别算出左下图中圆与正方形的面积比和右下图中圆与正方形的面积比并求出比值。如果图形的形状不变，正方形的边长及圆的半径发生变化，那么它们的比值会发生变化吗?(结果保留$\pi$)

答案： 7.π×$(\frac{8}{2})^2$=16π(cm²) 8×8=64(cm²) 比:
16π:64 比值:16π:64=$\frac{π}{4}$ π×6²=36π(cm²)
(6×2)²=144(cm²) 比:36π:144 比值:36π:
144=$\frac{π}{4}$ 如果图形的形状不变，正方形的边长及圆的半径发生变化，那么它们的比值不会发生变化
解析:分别求出图中圆与正方形的面积比并求出比值。设正方形的边长是a cm，则圆的半径是
$\frac{a}{2}$cm，圆的面积是π×$(\frac{a}{2})^2$=$\frac{πa^2}{4}$(cm²)，正方形的面积是a×a=a²(cm²)，圆与正方形的面积的比值是$\frac{πa^2}{4}$:a²=$\frac{π}{4}$，也就是无论正方形的边长是多少，圆与正方形的面积的比值都是$\frac{π}{4}$。