《2026年中考123试题精编物理》

28. (6分)一艘货轮在长江某河段行驶,50 s 内匀速通过200 m的路程,其牵引力为$5 × 10^{5} \ N$,求:
(1)货轮行驶的速度。
(2)牵引力做的功。
(3)牵引力的功率。

答案： 28.解：
(1)货轮行驶的速度：$v = \frac{s}{t} = \frac{200 m}{50 s} = 4 m/s$；
(2)牵引力做的功：$W = Fs = 5 × 10^{5} N × 200 m = 1 × 10^{8} J$；
(3)牵引力的功率：$P = \frac{W}{t} = \frac{1 × 10^{8} J}{50 s} = 2 × 10^{6} W$。
答：
(1)货轮行驶的速度是$4 m/s$；
(2)牵引力做的功是$1 × 10^{8} J$；
(3)牵引力的功率是$2 × 10^{6} W$。

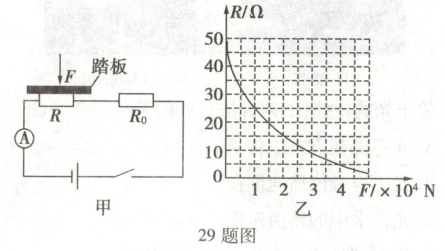
29. (8分)公路部门往往通过地磅检测汽车载重情况。图甲是跨学科学习团队设计的可视化地磅的电路原理图,主要由踏板(重力不计)、压力传感器 R、显示承重的仪表(实质为电流表,量程为$0 \sim 0.6 \ A$)等组成,R 的阻值与所受压力 F 的大小关系如图乙所示。电源电压为 12 V,定值电阻$R_0$的阻值为 5 $\Omega$。
(1)当 R 的阻值为 35 $\Omega$时,求电路的电流。
(2)当通过电路的电流为 0.4 A 时,求地磅的测量值。
(3)为了增加地磅的最大测量值,请你写出一种可行的方案,并列出关系式进行说明。

答案：
29.解：
(1)由图甲可知，$R$、$R_0$串联，电流表测量电路中的电流，当$R$的阻值为$35 \Omega$时，电路总电阻：$R_{ 总} = R + R_0 = 35 \Omega + 5 \Omega = 40 \Omega$，电路中的电流：$I = \frac{U}{R_{ 总}} = \frac{12 V}{40 \Omega} = 0.3 A$；
(2)当通过电路的电流为$0.4 A$时，电路的总电阻：$R_{ 总}' = \frac{U}{I'} = \frac{12 V}{0.4 A} = 30 \Omega$，$R$只与$R_0$串联，此时$R$的阻值：$R' = R_{ 总}' - R_0 = 30 \Omega - 5 \Omega = 25 \Omega$，由图乙可知，地磅受到的压力$F = 1 × 10^{4} N$，即地磅测量的重力$G = F = 1 × 10^{4} N$，则地磅的测量值：$m = \frac{G}{g} = \frac{1 × 10^{4} N}{10 N/kg} = 1000 kg$；
(3)要增大地磅的最大测量值，可行的方案是适当增大$R_0$的阻值(或适当减小电源电压或适当增大电流表的量程，写出任意一种即可)，根据图乙可知，$R$越小，$F$越大，由图甲可知，$R$越小，电流表示数越大，地磅测量值越大，当电流表示数达到最大测量值时，地磅测量值最大，设电流表的量程为$0 \sim I_{ max}$，地磅达到最大测量值时，根据欧姆定律可得，电路的总电阻$R_{ 总}'' = \frac{U}{I_{ max}}$，根据串联电路的电阻特点可知$R_{ 总}'' = R + R_0$，解得$R = \frac{U}{I_{ max}} - R_0$，由上式可知，$U$越小、$I_{ max}$越大、$R_0$越大，则$R$越小，因此，所选方案可行。
答：
(1)当$R$的阻值为$35 \Omega$时，电路的电流为$0.3 A$；
(2)当通过电路的电流为$0.4 A$时，地磅的测量值为$1000 kg$；
(3)要增大地磅的最大测量值，可行的方案是适当增大$R_0$的阻值(或适当减小电源电压或适当增大电流表的量程，写出任意一种即可)。

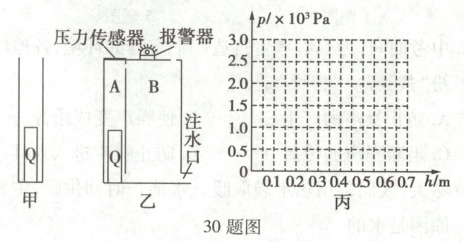
30. (10分)一个不吸水的实心圆柱体 Q,底面积为$0.01 \ m^2$,高为 0.3 m,密度为$0.5 × 10^{3} \ kg/m^3$。如图甲所示,现将 Q 放在容器中,缓慢往容器中注水(水的密度为$1.0 × 10^{3} \ kg/m^3$,$g$取 10 N/kg),求:
(1)圆柱体 Q 的质量。
(2)当注入水的深度为 0.1 m 时(此时 Q 未漂浮),Q 受到的浮力。
(3)广西夏季雨水充沛,每逢暴雨,河水水位快速上涨,为了监测河水水位,某项目小组设计了“智能水位报警器”,如图乙所示。其由 A、B 两部分组成,A 模拟控制器,B 模拟河道。其中 A 内部高度为 0.7 m,顶部固定着压力传感器,当压力达到某一数值时,报警器会自动报警。在某次注水测试中,当注水到某一深度时,Q 开始漂浮,随着注入水的深度增加,Q 最终会与传感器接触,当 Q 露出水面的长度为 0.1 m 时,报警器恰好开始报警。请通过计算,分析从开始注水到报警器报警的过程,并在丙图中作出此过程 Q 底部受到水的压强 p 随注入水的深度 h 变化的关系图线。

答案：
30.解：
(1)圆柱体Q的体积：$V = S_{ 圆} h = 0.01 m^2 × 0.3 m = 0.003 m^3$，圆柱体Q的质量：$m = \rho V = 0.5 × 10^{3} kg/m^3 × 0.003 m^3 = 1.5 kg$；
(2)当注入水的深度为$0.1 m$时，Q排开水的体积：$V_{ 排} = S_{ 圆} h_{ 水} = 0.01 m^2 × 0.1 m = 0.001 m^3$，此时圆柱体Q受到的浮力：$F_{ 浮} = \rho_{ 水} g V_{ 排} = 1.0 × 10^{3} kg/m^3 × 10 N/kg × 0.001 m^3 = 10 N$；
(3)注水深度为0时，圆柱体Q底部受到水的压强为0，圆柱体Q的重力：$G = mg = 1.5 kg × 10 N/kg = 15 N$，①圆柱体刚好漂浮时，$F_{ 浮1} = G = 15 N$，此时圆柱体排开水的体积：$V_1 = \frac{F_{ 浮1}}{\rho_{ 水} g} = \frac{15 N}{1.0 × 10^{3} kg/m^3 × 10 N/kg} = 0.0015 m^3$，注水的深度：$h_1 = \frac{V_1}{S_{ 圆}} = \frac{0.0015 m^3}{0.01 m^2} = 0.15 m$，圆柱体Q底部受到水的压强：$p_1 = \rho_{ 水} g h_1 = 1.0 × 10^{3} kg/m^3 × 10 N/kg × 0.15 m = 1500 Pa$，由上述计算可知，注入水的深度小于等于$0.15 m$的过程中，Q底部受到水的压强与注入水的深度成正比，故该过程$p - h$图线是一条过原点的倾斜线段；②继续注水，直到圆柱体Q的顶端刚好接触压力传感器时，注水的深度：$h_2 = h_A - (h_Q - h_1) = 0.7 m - (0.3 m - 0.15 m) = 0.55 m$，此时圆柱体Q底部受到水的压强：$p_2 = p_1 = 1500 Pa$，故注入水的深度从$0.15 m$到$0.55 m$的过程，$p - h$图线是一条水平线段；③继续注水，Q被传感器阻挡，不再上升，当圆柱体Q露出水面的长度为$0.1 m$时，注水的深度：$h' = h_A - 0.1 m = 0.7 m - 0.1 m = 0.6 m$，此时圆柱体Q浸在水中的深度：$h_3 = h_Q - 0.1 m = 0.3 m - 0.1 m = 0.2 m$，此时圆柱体Q底部受到水的压强：$p_3 = \rho_{ 水} g h_3 = 1.0 × 10^{3} kg/m^3 × 10 N/kg × 0.2 m = 2000 Pa$；由上述计算可知，注入水的深度从$0.55 m$到$0.6 m$的过程中，Q底部受到水的压强与Q浸入水中的深度成正比，故此过程$p - h$图线是一条倾斜线段，综合①②③，此过程Q底部受到水的压强$p$随注入水的深度$h$变化的关系图线如答图所示。

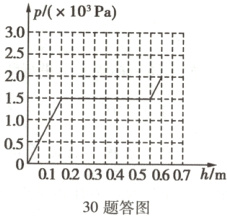
答：
(1)圆柱体Q的质量为$1.5 kg$；
(2)当注入水的深度为$0.1 m$时(此时Q未漂浮)，Q受到的浮力为$10 N$；
(3)如答图所示。