2026年中考123试题精编物理
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2026年中考123试题精编物理 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第35页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
17. 小明在伊通河畔拾到一块漂亮的小石块。他想通过测量密度鉴别小石块的材质。
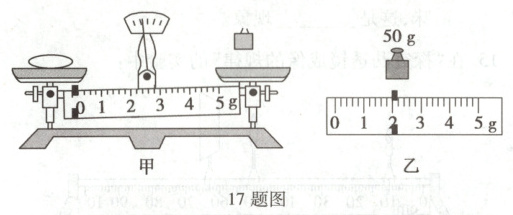
(1)用调好的天平测量小石块的质量时,操作如图甲所示,出现的错误是
(2)天平再次平衡时,盘中砝码的质量及游码的位置如图乙所示,小石块的质量为
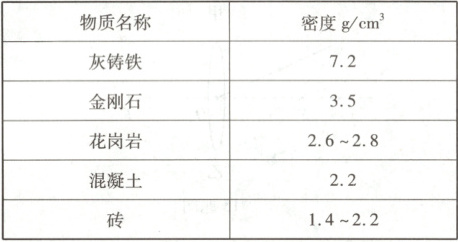
(3)用量筒测出小石块的体积为20 $cm^3$,计算出小石块的密度,与上表中的密度值对比后,初步判断小石块可能是


(1)用调好的天平测量小石块的质量时,操作如图甲所示,出现的错误是
用手拿砝码
。(2)天平再次平衡时,盘中砝码的质量及游码的位置如图乙所示,小石块的质量为
52
g。(3)用量筒测出小石块的体积为20 $cm^3$,计算出小石块的密度,与上表中的密度值对比后,初步判断小石块可能是
花岗岩
。
答案:
17.
(1)用手拿砝码
(2)52
(3)花岗岩
[解析]
(1)由图甲知,在称量过程中,小明用手拿砝码了,这样会造成砝码锈蚀;
(2)由图乙知,标尺的分度值为0.2g,小石块的质量m=50g+2g=52g;
(3)用量筒测出小石块的体积为20cm³,则小石块的密度为$\rho=\frac{m}{V}=\frac{52g}{20cm^{3}}=2.6g/cm^{3}$,与上表中的密度值对比后,初步判断小石块可能是花岗岩。
(1)用手拿砝码
(2)52
(3)花岗岩
[解析]
(1)由图甲知,在称量过程中,小明用手拿砝码了,这样会造成砝码锈蚀;
(2)由图乙知,标尺的分度值为0.2g,小石块的质量m=50g+2g=52g;
(3)用量筒测出小石块的体积为20cm³,则小石块的密度为$\rho=\frac{m}{V}=\frac{52g}{20cm^{3}}=2.6g/cm^{3}$,与上表中的密度值对比后,初步判断小石块可能是花岗岩。
18. 在“探究杠杆的平衡条件”的实验中:
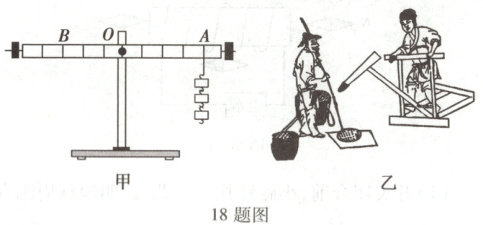
(1)不挂钩码时,调节螺母,使杠杆在
(2)如图甲所示,在 A 点挂3个钩码,在 B 点挂
(3)画出 A 点所受拉力的力臂$l$。
(4)如图乙所示是《天工开物》记载的踏碓(碓:duì,古代的一种给稻谷去壳的工具。用脚连续踏杆的一端,另一端就会连续起落)。踏碓属于

(1)不挂钩码时,调节螺母,使杠杆在
水平
位置平衡。(2)如图甲所示,在 A 点挂3个钩码,在 B 点挂
4
个钩码,使杠杆再次在原位置平衡。(3)画出 A 点所受拉力的力臂$l$。
(4)如图乙所示是《天工开物》记载的踏碓(碓:duì,古代的一种给稻谷去壳的工具。用脚连续踏杆的一端,另一端就会连续起落)。踏碓属于
费力
杠杆。
答案:
18.
(1)水平
(2)4
(3)如答图所示

(4)费力
18.
(1)水平
(2)4
(3)如答图所示

(4)费力
19. 如图是一种测定油箱内油量的装置。竖直放置的均匀圆弧形电阻丝 R 长20 cm,规格为1 Ω/cm。滑片 P 与滑杆连接,滑杆可绕固定轴 O 转动,O 是滑杆的中点,且与电阻丝 R 的中点在同一高度,滑杆的另一端通过轻质细杆连接一个浮子。油箱中的油量减少时,浮子随油面一起下降,带动滑杆使滑片向上移动,电流表的示数始终随之改变。

(1)油量逐渐减少,电阻$R_0$两端的电压逐渐
(2)当油箱加满油时,滑片刚好位于 R 的下端,电流表指针指在最大刻度处,此时示数为0.6 A;油面缓慢下降,当 R 接入电路的长度为4 cm 时,电流表示数为0.3 A;油面继续缓慢下降到最低位置时(油箱底部还有少许油可忽略不计),滑片刚好位于 R 的上端。电源电压为
(3)对(2)中的设计进行调整,在保证油箱加满油时,电流表指针仍指在最大刻度的前提下,只改变电阻$R_0$和电源电压,就能实现还剩半箱油时,指针刚好指在电流表表刻度的中央。则电阻$R_0$的阻值为

(1)油量逐渐减少,电阻$R_0$两端的电压逐渐
减小
。(2)当油箱加满油时,滑片刚好位于 R 的下端,电流表指针指在最大刻度处,此时示数为0.6 A;油面缓慢下降,当 R 接入电路的长度为4 cm 时,电流表示数为0.3 A;油面继续缓慢下降到最低位置时(油箱底部还有少许油可忽略不计),滑片刚好位于 R 的上端。电源电压为
2.4
V。(3)对(2)中的设计进行调整,在保证油箱加满油时,电流表指针仍指在最大刻度的前提下,只改变电阻$R_0$和电源电压,就能实现还剩半箱油时,指针刚好指在电流表表刻度的中央。则电阻$R_0$的阻值为
10
Ω。
答案:
19.
(1)减小
(2)2.4
(3)10
(1)减小
(2)2.4
(3)10
20. 学习浮力知识后,小明做了以下实验:将30 cm高的长方体 A 竖直放在圆柱形容器内。
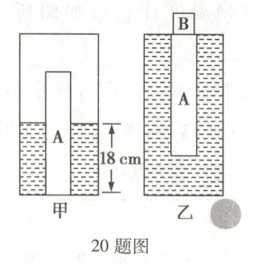
(1)向容器内缓慢注水,当长方体 A 刚好对容器底部无压力时,停止注水,水深为18 cm,如图甲所示。这一过程中,随着注水深度的增加,长方体 A 所受的浮力逐渐
(2)继续向容器内缓慢注水,直到注满。关于长方体 A 浸在水中的深度 h 与新注入水的质量 m 之间的关系,下列图像表达正确的是
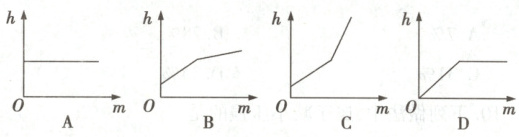
(3)将长方体 A 与合金块 B($\rho_B=6\rho_{水}$)粘合成一个整体,放入水中静止后,长方体 A 刚好浸没,如图乙所示。再将这个整体倒立放入水中,松手后这个整体保持竖直静止状态,求该状态下长方体 A 的底面所在深度处水的压强。(写出必要的文字说明、表达式及最后结果。已知:$\rho_{水}=1.0 × 10^3 kg/m^3$,$g = 10 N/kg$,粘合剂的质量与体积忽略不计)

(1)向容器内缓慢注水,当长方体 A 刚好对容器底部无压力时,停止注水,水深为18 cm,如图甲所示。这一过程中,随着注水深度的增加,长方体 A 所受的浮力逐渐
变大
。(2)继续向容器内缓慢注水,直到注满。关于长方体 A 浸在水中的深度 h 与新注入水的质量 m 之间的关系,下列图像表达正确的是
A
。
(3)将长方体 A 与合金块 B($\rho_B=6\rho_{水}$)粘合成一个整体,放入水中静止后,长方体 A 刚好浸没,如图乙所示。再将这个整体倒立放入水中,松手后这个整体保持竖直静止状态,求该状态下长方体 A 的底面所在深度处水的压强。(写出必要的文字说明、表达式及最后结果。已知:$\rho_{水}=1.0 × 10^3 kg/m^3$,$g = 10 N/kg$,粘合剂的质量与体积忽略不计)
答案:
20.
(1)变大
(2)A
解:
(3)设长方体A底面积为S,
由
(2)可知,$G_{A}=F_{浮1}=\rho_{水}gS h$①,
将长方体A与合金块B($\rho_{B}=6\rho_{水}$)粘合成一个整体,放入水中静止后,长方体A刚好浸没,此时长方体A受到的浮力等于长方体A、合金块B的重力,即:
$G_{A}+G_{B}=F_{浮2}=\rho_{水}gSH$②,
由①②可知,合金块B的重力:
$G_{B}=F_{浮2}-F_{浮1}=\rho_{水}gS(H - h)$,
根据重力公式结合密度公式可知,
$G_{B}=\rho_{B}gV_{B}=\rho_{水}gS(H - h)=\rho_{水}gS(0.3m - 0.18m)$,
解得$V_{B}=0.02m× S$,
当将这个整体倒立放入水中时,这个整体仍然处于漂浮状态,此时合金块B完全浸没在水中,长方体A浸没深度为$H'$,根据浮沉条件可知,
$G_{A}+G_{B}=F_{浮3}+F_{浮B}=\rho_{水}gSH'+ \rho_{水}gV_{B}=\rho_{水}gSH'+0.02m×\rho_{水}gS$③,
由②③可得:
$\rho_{水}gSH=\rho_{水}gSH'+0.02m×\rho_{水}gS$,即$0.3m=H'+0.02m$,
解得$H'=0.28m$,
根据液体压强公式可知,该状态下长方体A的底面所在深度处水的压强:$p=\rho_{水}gH'=1.0×10^{3}kg/m^{3}×10N/kg×0.28m=2.8×10^{3}Pa$。
答:该状态下长方体A底面所在深度处水的压强为$2.8×10^{3}Pa$。
(1)变大
(2)A
解:
(3)设长方体A底面积为S,
由
(2)可知,$G_{A}=F_{浮1}=\rho_{水}gS h$①,
将长方体A与合金块B($\rho_{B}=6\rho_{水}$)粘合成一个整体,放入水中静止后,长方体A刚好浸没,此时长方体A受到的浮力等于长方体A、合金块B的重力,即:
$G_{A}+G_{B}=F_{浮2}=\rho_{水}gSH$②,
由①②可知,合金块B的重力:
$G_{B}=F_{浮2}-F_{浮1}=\rho_{水}gS(H - h)$,
根据重力公式结合密度公式可知,
$G_{B}=\rho_{B}gV_{B}=\rho_{水}gS(H - h)=\rho_{水}gS(0.3m - 0.18m)$,
解得$V_{B}=0.02m× S$,
当将这个整体倒立放入水中时,这个整体仍然处于漂浮状态,此时合金块B完全浸没在水中,长方体A浸没深度为$H'$,根据浮沉条件可知,
$G_{A}+G_{B}=F_{浮3}+F_{浮B}=\rho_{水}gSH'+ \rho_{水}gV_{B}=\rho_{水}gSH'+0.02m×\rho_{水}gS$③,
由②③可得:
$\rho_{水}gSH=\rho_{水}gSH'+0.02m×\rho_{水}gS$,即$0.3m=H'+0.02m$,
解得$H'=0.28m$,
根据液体压强公式可知,该状态下长方体A的底面所在深度处水的压强:$p=\rho_{水}gH'=1.0×10^{3}kg/m^{3}×10N/kg×0.28m=2.8×10^{3}Pa$。
答:该状态下长方体A底面所在深度处水的压强为$2.8×10^{3}Pa$。
查看更多完整答案,请扫码查看


