《2026年中考123试题精编物理》

17. 在“探究什么情况下磁可以生电”的实验中：

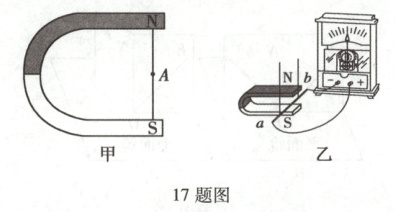
(1) 请在图甲中标出经过A点的磁感线的方向。
(2) 如图乙所示,将闭合电路中的导线$ab$放在蹄形磁体的磁场中,导线$ab$左右运动时,电流表指针偏转。这一过程中,该装置将机械能转化为电能。这一现象在生活中的应用有发电机。

答案：
17.
(1)如答图所示

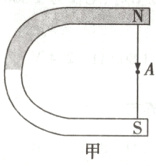
(2)偏转 机械能 发电机

18. 在“探究杠杆的平衡条件”的实验中,每个钩码重相同。

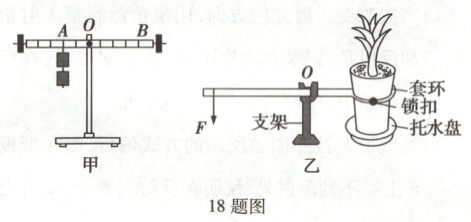
(1) 实验前,调节螺母,使杠杆在水平位置平衡。
(2) 如图甲所示,在杠杆A点挂2个钩码,B点挂1个钩码,才能使杠杆再次在水平位置平衡。多次实验后,得出杠杆的平衡条件为动力×动力臂 = 阻力×阻力臂。
(3) 小明看到爸爸利用图乙的“帮手”抬起大花盆,取出托水盘清洗。为了抬起花盆时更省力,他建议爸爸将支架向右移动一些距离。
(4) 请在图乙中画出动力F的力臂l的示意图。

答案：
18.
(2)1 动力×动力臂 = 阻力×阻力臂
(3)右
(4)如答图所示

19. 某同学为探究影响浮力大小的因素,准备了大容器、高为h的柱形金属块和高为4h的柱形小桶,小桶的底面积是金属块底面积的2倍(不计小桶的质量和厚度,桶壁刻度均匀),探究过程如下：

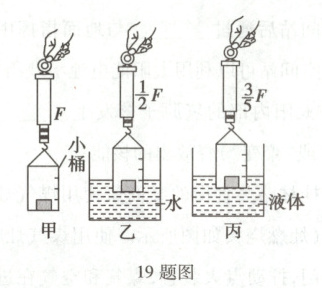
(1) 如图甲所示,将金属块放入小桶静止后,弹簧测力计示数为F。
(2) 如图乙所示,使小桶浸入水中的深度为h时静止,弹簧测力计示数为$\frac{1}{2}F$。
(3) 如图丙所示,使小桶浸入某种液体($\rho_{液}$＜$\rho_{水}$)中的深度为h时静止,弹簧测力计示数为$\frac{3}{5}F$。
小桶在图乙、图丙中所受浮力分别为$F_乙$、$F_丙$,其大小关系为$F_乙$＞$F_丙$,说明浮力的大小与液体密度有关。
(4) 在(3)的基础上,向小桶内缓慢加水,小桶底部所受水的压强逐渐变大。小桶内水的深度为H时停止加水,调节弹簧测力计的高度,使小桶浸入液体中的深度为2h时静止(小桶未触底),弹簧测力计示数为$\frac{1}{2}F$,则$H:h$=11:10。

答案： 19.
(3)＞ 液体密度
(4)变大 $11:10$
[解析]
(1)如图甲所示，将金属块放入小桶静止后，弹簧测力计示数为$F$，由于不计小桶的质量和厚度，则金属块的重力：$G = F$；
(2)如图乙所示，使小桶浸入水中的深度为$h$时静止，弹簧测力计示数为$\frac{1}{2}F$，此时小桶在水中受到的浮力：$F_{浮} = G - \frac{1}{2}F = F - \frac{1}{2}F = \frac{1}{2}F$；
(3)如图丙所示，使小桶浸入某种液体($\rho_{液} ＜ \rho_{水}$)中的深度为$h$时静止，弹簧测力计示数为$\frac{3}{5}F$，此时小桶在该液体中受到的浮力：$F_{浮液} = G - \frac{3}{5}F = F - \frac{3}{5}F = \frac{2}{5}F$，则$F_{浮乙} ＞ F_{浮液}$；由于小桶在两种液体中浸入的深度相同，即小桶排开液体的体积相同，说明浮力的大小与液体密度有关；
(4)在
(3)的基础上，向小桶内缓慢加水，小桶内水的深度增加，小桶底部所受水的压强逐渐变大；当小桶内水的深度为$H$时停止加水，调节弹簧测力计的高度，使小桶浸入液体中的深度为$2h$时静止(小桶未触底)，弹簧测力计示数为$\frac{1}{2}F$，则此时小桶受到的浮力：$F_{浮} = G_{水} + G - \frac{1}{2}F = G_{水} + \frac{1}{2}F$，而此时排开液体的体积是
(3)中的$2$倍，则$F_{浮} = 2F_{浮液} = 2 × \frac{2}{5}F = \frac{4}{5}F$，则$G_{水} + \frac{1}{2}F = \frac{4}{5}F$，则$G_{水} = \frac{3}{10}F$，设金属块的底面积为$S$，则小桶的底面积为$2S$，在
(2)中，由阿基米德原理可得，小桶在水中受到的浮力：$F_{浮乙} = \rho_{水}gh · 2S = 2\rho_{水}ghS = \frac{1}{2}F ①$，假设$H \leq h$，则加入小桶中水受到的重力：$G_{水} = \rho_{水}HSg = \frac{3}{10}F ②$，由$ ①②$可得$\frac{2\rho_{水}ghS}{\rho_{水}HSg} = \frac{\frac{1}{2}F}{\frac{3}{10}F} = \frac{5}{3}$，即$\frac{H}{h} = \frac{6}{5}$，与假设不符；假设$H ＞ h$，则加入小桶中水受到的重力：$G_{水} = \rho_{水}(2HS - hS)g = \rho_{水}(2H - h)Sg = \frac{3}{10}F ③$，由$ ①③$可得$\frac{2\rho_{水}ghS}{\rho_{水}(2H - h)Sg} = \frac{\frac{1}{2}F}{\frac{3}{10}F}$，即$\frac{H}{h} = \frac{11}{10}$，与假设相符。

20. 鉴定牛奶、酒的品质,农业选种时配制盐水等,都需要测量密度。为此,某科技小组设计了一款多量程密度计,其示意图如图甲所示。电源电压恒定不变,电流表量程选用0～0.6 A,将电流值标记为对应的液体密度值。压敏电阻$R_1$所受压力每增加1 N,阻值减小6.25 Ω；压敏电阻$R_2$所受压力每增加1 N,阻值减小$\Delta R$,实验中$R_1$、$R_2$的阻值随压力变化的规律不变。(装置中杯子质量忽略不计,$\rho_{水}=1.0 g/cm^3$,$g=10 N/kg$)

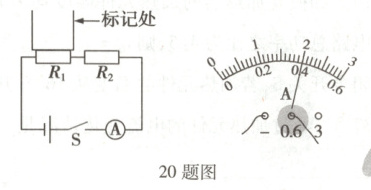
(1) 闭合开关,电流表示数如图乙所示,为0.4A；将杯子放在$R_1$上,向杯子中缓慢注入重1.6 N、密度为1.6$g/cm^3$的液体,在杯子外表面标记出液面位置,此时$R_1$的阻值为2 Ω,电流表示数为0.6 A,则$R_1$不受压力时的阻值为12Ω,电源两端的电压为12V。
(2) 倒出杯子中的液体,将杯子擦干放在$R_2$上,向杯子中缓慢注入水,使水面到达标记处,电流表示数为0.6 A；如果杯子放在$R_2$上时缓慢注入另一种液体,液面到达标记处时,电流表示数为0.5 A,则这种液体的密度应为0.6$g/cm^3$。
(3) 分析发现,与杯子放在$R_1$上制作的密度计相比较,杯子放在$R_2$上制作的密度计的优点是可以使两条刻度线之间的距离大一些，测量结果会更准确。

答案： 20.
(1)$0.4\ 12\ 12$
(2)$0.6$
(3)可以使两条刻度线之间的距离大一些，测量结果会更准确
[解析]由电路图可知，$R_1$与$R_2$串联，电流表测电路中的电流。
(1)由图乙可知，电流表的量程为$0\sim0.6\ A$，分度值为$0.02\ A$，示数$I_1 = 0.4\ A$，将杯子放在$R_1$上，向杯子中缓慢注入重$1.6\ N$的液体，在杯子外表面标记出液面位置，此时$R_1$的阻值为$2\ \Omega$，电流表示数$I_2 = 0.6\ A$，因串联电路中总电压等于各分电压之和，串联电路总电阻等于各分电阻之和，串联电路各处电流相等，所以，由$I = \frac{U}{R}$可得，电源的电压$U = I_2R_{总} = I_2(R_1 + R_{20}) = 0.6\ A × (2\ \Omega + R_{20}) ①$，因压敏电阻$R_1$所受压力每增加$1\ N$，阻值减小$6.25\ \Omega$，所以$R_1$不受压力时的阻值：$R_{10} = R_1 + 1.6\ N × 6.25\ \Omega/N = 2\ \Omega + 10\ \Omega = 12\ \Omega$，则$U = I_1R_{总} = I_1(R_{10} + R_{20}) = 0.4\ A × (12\ \Omega + R_{20}) ②$，由$ ①②$可得$U = 12\ V$，$R_{20} = 18\ \Omega$；
(2)倒出杯子中的液体，将杯子擦干放在$R_2$上，向杯子中缓慢注入水，使水面到达标记处，则液体的体积不变，由$G = mg = \rho Vg$的变形式$V = \frac{G}{\rho g}$可得$\frac{G_{液}}{\rho_{液}g} = \frac{G_{水}}{\rho_{水}g}$，则压敏电阻$R_2$所受压力：$F_{水} = G_{水} = \frac{\rho_{水}}{\rho_{液}}G_{液} = \frac{1.0\ g/cm^3}{1.6\ g/cm^3} × 1.6\ N = 1\ N$，此时电流表示数为$0.6\ A$，电路的总电阻为$R_{总}'$，则$R_1 + R_{20} = R_{10} + R_2$，即$2\ \Omega + 18\ \Omega = 12\ \Omega + R_2$，解得$R_2 = 8\ \Omega$，所以，压敏电阻$R_2$所受压力每增加$1\ N$，阻值减小$\Delta R = R_{20} - R_2 = 18\ \Omega - 8\ \Omega = 10\ \Omega$；如果杯子放在$R_2$上时缓慢注入另一种液体，液面到达标记处时，电流表示数为$0.5\ A$，此时电路的总电阻：$R_{总}'' = \frac{U}{I_3} = \frac{12\ V}{0.5\ A} = 24\ \Omega$，此时压敏电阻$R_2$的阻值：$R_2' = R_{总}'' - R_{10} = 24\ \Omega - 12\ \Omega = 12\ \Omega$，压敏电阻$R_2$所受压力：$F_{液}' = \frac{R_{20} - R_2'}{10\ \Omega/N} = \frac{18\ \Omega - 12\ \Omega}{10\ \Omega/N} = 0.6\ N$，由$V = \frac{G}{\rho g}$可得$\frac{G_{液}}{\rho_{液}g} = \frac{G_{液}'}{\rho_{液}'g}$，解得$\rho_{液}' = \frac{G_{液}'}{G_{液}}\rho_{液} = \frac{0.6\ N}{1.6\ N} × 1.6\ g/cm^3 = 0.6\ g/cm^3$；
(3)因压敏电阻$R_1$所受压力每增加$1\ N$时阻值减小$6.25\ \Omega$，压敏电阻$R_2$所受压力每增加$1\ N$时阻值减小$10\ \Omega$，所以，由欧姆定律可知，测量相同液体密度时，杯子放在$R_2$上制作的密度计，会使电路中的电流变化比较明显，可以使两条刻度线之间的距离大一些，测量结果会更准确。