《2026年高考一线课时练习高中物理必修第一册通用版江苏专版》

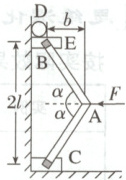
例③ 如图所示是扩张机的原理示意图，$A$、$B$为活动铰链，$C$为固定铰链，在$A$处作用一水平力$F$，滑块$E$就以比$F$大得多的压力向上顶物体$D$，已知图中$2l = 1.0\ m$，$b = 0.05\ m$，$F = 400\ N$，滑块$E$与墙壁接触，接触面光滑，则物体$D$受到向上顶的力为(滑块和杆所受的重力不计) (B)


A.3000 N
B.2000 N
C.1000 N
D.500 N

答案： 例3　B　将F沿AC、AB方向分解为F₁、F₂，则F₂=$\frac{F}{2cos\alpha}$，F₂的作用效果是使滑块E对墙壁有水平向左的挤压作用F₃，对物体D有竖直向上的挤压作用F₄，则物体D所受的向上顶的力为F_N=F₄=F₂sin$\alpha$=$\frac{F}{2}$tan$\alpha$，由题图可知tan$\alpha$=$\frac{l}{b}$=$\frac{0.5}{0.05}$=10，故F_N=2000N，选项B正确。

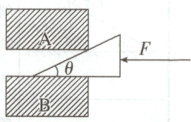
4. 人们把截面如图所示的斜面体木料叫作楔。明朝年间，苏州的虎丘寺塔因年久失修，塔身倾斜，有倒塌的危险。有一位和尚把木楔一个一个地从塔身倾斜的一侧的砖缝间敲进去，结果扶正了塔身。假设和尚所用的木楔表面光滑、质量不计，木楔的一个角为$\theta$，如图所示，现在木楔背上加一压力$F$，使木楔保持静止，则 (C)


A.木楔对$A$砖块的压力大小为$F\sin\theta$
B.木楔对$A$砖块的压力大小为$\frac{F}{\cos\theta}$
C.木楔对$B$砖块的压力大小为$\frac{F}{\tan\theta}$
D.木楔对$B$砖块的压力大小为$F\tan\theta$

答案：
4.C对压力F进行分解如图所示，根据几何知识可
　　　　　　　　　　　　　　　　　　　　
得，木楔对A砖块的压力大小为F₁=$\frac{F}{sin\theta}$，对B砖块的压力大小为F₂=$\frac{F}{tan\theta}$，故C正确，A、B、D错误。

例④ 在同一平面内共点的四个力$F_1$、$F_2$、$F_3$、$F_4$的大小依次为19 N、40 N、30 N和15 N，方向如图所示，求它们的合力。($\cos37^{\circ}=0.8$，$\sin37^{\circ}=0.6$)

[尝试解答]

答案：
解析:如图甲建立直角坐标系，把各个力分解在两个坐标轴上,并求出x轴和y轴上的合力Fₓ和F_y，有
Fₓ=F₁+F₂cos 37°-F₃cos 37°=27 N
F_y=F₂sin 37°+F₃sin 37°-F₄=27 N
　　　　　 　
因此，如图乙所示，合力F=$\sqrt{Fₓ²+F_y²}$≈38.2 N，tan$\varphi$=$\frac{F_y}{Fₓ}$=1
即合力的大小约为38.2 N，方向与F₁夹角为45°，斜向右上方。
答案:38.2 N　与F₁夹角为45°，斜向右上方

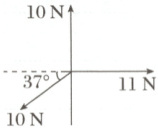
5. 在同一平面内作用着三个共点力，它们的大小和方向如图所示。已知$\sin37^{\circ}=0.6$，$\cos37^{\circ}=0.8$，则这三个力的合力大小为 (A)


A.5 N
B.$\sqrt{139}\ N$
C.$\sqrt{29}\ N$
D.7 N

答案：
5.A　如图所示，以三力共同作用点为原点，竖直方向为y轴，水平方向为x轴建立坐标系，则x轴方向上的合力大小
　　　　　　　　　　　　　　　
为Fₓ=11N - 10N·cos 37°=3N，y轴方向上的合力大小为F_y=10N - 10N·sin 37°=4N，这三个力的合力大小为F=$\sqrt{Fₓ²+F_y²}$=5N，故A正确。