《2026年高考一线课时练习高中物理必修第一册通用版江苏专版》

例② 某同学探究弹簧弹力与形变量的关系。
(1)将弹簧悬挂在铁架台上，将刻度尺固定在弹簧一侧。弹簧轴线和刻度尺都应在竖直方向(选填“水平”或“竖直”)。
(2)弹簧自然悬挂，待弹簧静止时，长度记为$L_0$；弹簧下端挂上砝码盘时，弹簧长度记为$L_x$；在砝码盘中每次增加 10 g 砝码，弹簧长度依次记为$L_1$至$L_6$。数据如下表。

表中有一个数值记录不规范，代表符号为$L_3$；由表可知所用刻度尺的最小分度为1 mm。
(3)如图甲所示是该同学根据表中数据作出的图线，纵轴是砝码的质量，横轴是弹簧长度与$L_x$的差值(填“$L_0$”或“$L_x$”)。

(4)由图甲可知弹簧的劲度系数为4.9$N/m$；通过图和表可知砝码盘的质量为10g。(结果保留两位有效数字，重力加速度 $g$ 取$9.8 N/kg$)
(5)如图乙所示是另一组同学实验得到弹簧弹力 $F$ 与弹簧伸长量 $x$ 的 $F - x$ 图线，由此可求出该组同学所用弹簧的劲度系数为200$N/m$(结果保留三位有效数字)，图线不过原点的原因是由于弹簧自身存在重力。

答案： 解析：
(1)为保证弹簧的拉力与砝码盘和砝码的重力大小相等，弹簧轴线和刻度尺均应在竖直方向。
(2)弹簧静止稳定时，记录原长$L_0$；表中的数据$L_3$与其他数据有效数字位数不同，所以数据$L_3$记录不规范，标准数据应读至cm单位的后两位小数，最后一位应为估读值，所以刻度尺的最小分度为1mm。
(3)由题图知所挂砝码质量为0时，x为0，所以$x = L - L_x$（L为弹簧长度）。
(4)由胡克定律$F = k\Delta x$知，$mg = k(L - L_x)$，即$mg = kx$，所以图线斜率为$\frac{k}{g}$，则弹簧的劲度系数$k = \frac{\Delta mg}{\Delta x} = \frac{(60 - 10) × 10^{-3} × 9.8}{(12 - 2) × 10^{-2}} N/m = 4.9 N/m$，同理砝码盘的质量$m_0 = \frac{k(L_x - L_0)}{g} = \frac{4.9 × (27.35 - 25.35) × 10^{-2}}{9.8} kg = 0.01 kg = 10 g$。
(5)图像中的斜率表示弹簧的劲度系数，则题图乙中的弹簧的劲度系数$k = \frac{7}{(4 - 0.5) × 10^{-2}} N/m = 200 N/m$；图线不过原点说明没有力时弹簧有了形变量，故说明弹簧有自身的重力存在。
答案：
(1)竖直
(2)静止 $L_3$ 1 mm
(3)$L_x$
(4)4.9 10
(5)200 弹簧自身存在重力

例③ 某同学在研究性学习中，利用所学的知识解决了如下问题：把一开口向右、内壁光滑、深度为 $h = 0.25 m$ 的小圆筒水平固定在桌面上，同时把一轻弹簧一端固定于小圆筒内部左端，没有外力作用时弹簧的另一端位于筒内，如图甲所示。如果本实验的长度测量工具只能测量出筒外弹簧的长度 $l$，现要测出弹簧的原长 $l_0$ 和弹簧的劲度系数，该同学通过改变所挂钩码的个数来改变 $l$，作出 $F - l$ 图线如图乙所示。

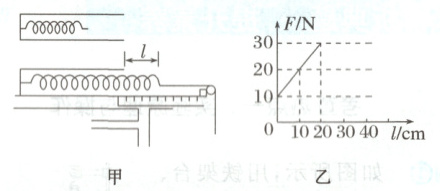
(1)由此图线可得出的结论是弹簧弹力和弹簧形变量成正比。
(2)弹簧的劲度系数为100$N/m$，弹簧的原长 $l_0 =$0.15$m$。
(3)该同学实验时，把弹簧水平放置与弹簧竖直悬挂放置相比较，优点在于水平放置可以消除由于弹簧自身重力造成的误差。

答案： 解析：
(1)从乙图中可以看出$\frac{\Delta F}{\Delta l}$为定值，即弹簧弹力和弹簧形变量成正比。
(2)当外力为零时弹簧的长度为弹簧原长，根据胡克定律可得$F = k(h + l - l_0) = kl + k(h - l_0)$，图乙中的斜率表示弹簧的劲度系数，故有$k = \frac{\Delta F}{\Delta l} = \frac{30 - 10}{(20 - 0) × 10^{-2}} N/m = 100 N/m$，从乙图中得出当$l = 0$时，$F = 10 N$，可得$l_0 = 0.15 m$。
(3)该同学实验时，把弹簧水平放置与弹簧竖直悬挂放置相比较，优点在于避免弹簧自身所受重力对实验的影响。
答案：
(1)弹簧弹力和弹簧形变量成正比
(2)100 0.15
(3)水平放置可以消除由于弹簧自身重力造成的误差