《2026年决胜中考物理安徽专版》

1. (2025·深圳)如图是深圳号在海上航行，田田同学乘坐了这艘船出海游玩。田田发现这艘船最大吃水高度是 $ 9 \, m $，最大排水量是 $ 70000 \, t $，船上一汽车用钢打造，钢的体积为 $ 0.1 \, m^3 $。(已知:钢的密度是 $ 7.9 × 10^3 \, kg/m^3 $，海水密度是 $ 1 × 10^3 \, kg/m^3 $，$ g = 10 \, N/kg $)求:
(1)钢的质量。
(2)求轮船满载时所受的浮力。
(3)船底面积是 $ 1 × 10^3 \, m^2 $，求轮船底部受到的压力。

答案： 1.解：
(1)钢的质量$m_{钢}=\rho_{钢} V_{钢}=7.9 × 10^{3} kg/m^{3} × 0.1 m^{3}=790 kg$。
(2)根据阿基米德原理可得，轮船满载时所受的浮力$F_{浮}=G_{排}=m_{排}g=70 000 × 10^{3} kg × 10 N/kg=7 × 10^{8} N$。
(3)轮船底部受到的海水压强$p=\rho gh=1 × 10^{3} kg/m^{3} × 10 N/kg × 9 m=9 × 10^{4} Pa$，轮船底部受到的压力$F=pS=9 × 10^{4} Pa × 1 × 10^{3} m^{2}=9 × 10^{7} N$。

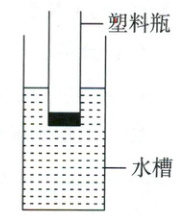
2. (2025·乐山)如图所示，某同学用一个上端开口的圆柱形厚底空塑料瓶和装有水的圆柱形水槽制作了一个浮力秤，用于测量质量。空塑料瓶质量为 $ 120 \, g $，塑料瓶底面积为 $ 20 \, cm^2 $，水槽底面积为 $ 120 \, cm^2 $，瓶身能够浸入水中的最大长度为 $ 18 \, cm $，使用过程中水不溢出，塑料瓶始终漂浮且瓶身保持竖直。已知水的密度为 $ 1.0 × 10^3 \, kg/m^3 $，$ g $ 取 $ 10 \, N/kg $，不考虑塑料瓶侧壁的厚度。求:
(1)空载时塑料瓶受到的浮力。
(2)浮力秤的最大称量值。
(3)浮力秤空载时和最大称量时水槽内水面的高度差。

答案： 2.解：
(1)空塑料瓶的重力$G_{瓶}=m_{瓶}g=120 × 10^{-3} kg ×10 N/kg=1.2 N$。由于漂浮，空载时塑料瓶受到的浮力，即$F_{浮1}=G_{瓶}=1.2 N$。
(2)当塑料瓶满载时，浸入水中深度最大，此时塑料瓶排开水的体积$V_{排}=S_{瓶}h=20 × 10^{-4} m^{2} × 18 × 10^{-2} m=3.6 ×10^{-4} m^{3}$，此时塑料瓶受到的浮力$F_{浮2}=\rho_{水}gV_{排}=1.0 ×10^{3} kg/m^{3} × 10 N/kg × 3.6 × 10^{-4} m^{3}=3.6 N$，此时所载物体的重力$G_{物}=F_{浮2}-G_{瓶}=3.6 N - 1.2 N=2.4 N$，浮力称的最大称量值$m_{最大}=\frac{G_{物}}{g}=\frac{2.4 N}{10 N/kg}=0.24 kg$。
(3)浮力秤空载时和最大称量时塑料瓶浸入水中的体积变化量$\Delta V=\frac{\Delta F_{浮}}{\rho_{水}g}=\frac{F_{浮2}-F_{浮1}}{\rho_{水}g}=\frac{3.6 N - 1.2 N}{1.0 × 10^{3} kg/m^{3} × 10 N/kg}=2.4 × 10^{-4} m^{3}$，水槽内水面的高度差$\Delta h=\frac{\Delta V}{S_{瓶}}=\frac{2.4 × 10^{-4} m^{3}}{120 × 10^{-4} m^{2}}=0.02 m$。

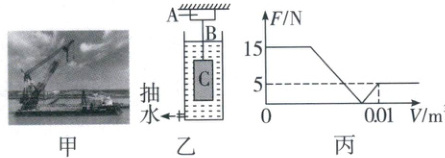
3. (2025·德阳)如图甲所示，“国之重器”起重船起吊重物时，需通过抽水机将一侧水舱里的水抽向另一侧水舱来保持起重船平衡。如图乙所示，小兰设计了一种采用力传感器感知抽水量的长方体水舱模型，水舱中装有 $ V = 0.014 \, m^3 $ 的水，其底面积 $ S = 0.04 \, m^2 $。A 是固定在顶端的力传感器，能够显示 A 对 B 的压力或拉力的大小;B 是质量和体积均可忽略的细直硬杆，不考虑 B 的形变，B 的上端与力传感器 A 连接，下端与物体 C 连接;物体 C 是质量 $ m = 0.5 \, kg $、底面积 $ S_{C} = 0.01 \, m^2 $ 的圆柱体。用抽水机将水抽出的过程中，力传感器示数 $ F $ 的大小随抽出水的体积 $ V $ 变化的图像如图丙所示。当物体 C 的下端刚好露出水面，此时已抽出水的体积 $ V_{抽} = 0.01 \, m^3 $。已知 $ \rho_{水} = 1.0 × 10^3 \, kg/m^3 $，$ g = 10 \, N/kg $。求:
(1)物体 C 的重力。
(2)物体 C 完全浸没时排开水的体积。
(3)当力传感器示数为 $ 2 \, N $ 时，水对水舱模型底部的压强。

答案： 3.解：
(1)物体C的重力$G=mg=0.5 kg × 10 N/kg=5 N$。
(2)当物体C完全浸没时，由题图丙可知杆对物体C的压力$F=15 N$，对C受力分析，则$F_{浮}=G + F=5 N + 15 N=20 N$，则物体C完全浸没时排开水的体积$V_{排}=\frac{F_{浮}}{\rho_{水}g}=\frac{20 N}{1.0 × 10^{3} kg/m^{3} × 10 N/kg}=2 × 10^{-3} m^{3}$。
(3)当物体C的下端刚好露出水面时，水舱模型内剩余水的体积$V_{水}=V - V_{排}=0.014 m^{3} - 0.01 m^{3}=0.004 m^{3}$，C的下端距离水舱模型底部的距离$h_{0}=\frac{V_{水}}{S_{C}}=\frac{0.004 m^{3}}{0.04 m^{2}}=0.1 m$。当力传感器示数为$2 N$时，有以下两种情况：①若杆对物体C的压力为$F_{1}=2 N$，$F_{浮1}=G + F_{1}=5 N + 2 N=7 N$，物体C排开水的体积$V_{排1}=\frac{F_{浮1}}{\rho_{水}g}=\frac{7 N}{1.0 × 10^{3} kg/m^{3} × 10 N/kg}=7 × 10^{-4} m^{3}$，物体C浸在水中的深度$h_{1}=\frac{V_{排1}}{S_{C}}=\frac{7 × 10^{-4} m^{3}}{0.01 m^{2}}=0.07 m$，此时水的深度$H_{1}=h_{1} + h_{0}=0.07 m + 0.1 m=0.17 m$，则水对水舱模型底部的压强$p_{1}=\rho_{水}gH_{1}=1 × 10^{3} kg/m^{3} × 10 N/kg ×0.17 m=1.7 × 10^{3} Pa$。②若杆对物体C的拉力为$F_{2}=2 N$，则$F_{浮2}=G - F_{2}=5 N - 2 N=3 N$，物体C排开水的体积$V_{排2}=\frac{F_{浮2}}{\rho_{水}g}=\frac{3 N}{1.0 × 10^{3} kg/m^{3} × 10 N/kg}=3 × 10^{-4} m^{3}$，物体C浸在水中的深度$h_{2}=\frac{V_{排2}}{S_{C}}=\frac{3 × 10^{-4} m^{3}}{0.01 m^{2}}=0.03 m$，此时水的深度$H_{2}=h_{2} + h_{0}=0.03 m + 0.1 m=0.13 m$，则水对水舱模型底部的压强$p_{2}=\rho_{水}gH_{2}=1 × 10^{3} kg/m^{3} ×10 N/kg × 0.13 m=1.3 × 10^{3} Pa$，所以当力传感器示数为$2 N$时，水对水舱模型底部的压强为$1.7 × 10^{3} Pa$或$1.3 ×10^{3} Pa$。