《2025年小题狂做高中数学选择性必修第二册苏教版》

1. (2024江苏连云港期中)在空间直角坐标系中，点$ A(2,1,1) $关于$ yOz $平面对称的点的坐标为(A)

A.$ (-2,1,1) $
B.$ (2,-1,1) $
C.$ (2,1,-1) $
D.$ (2,-1,-1) $

答案： 1.A在空间直角坐标系中，点A(2,1,1)关于yOz平面对称的点坐标为(-2,1,1).
方法总结：空间点的对称问题
(1)空间直角坐标系中对称点的坐标：
①点(a,b,c)关于原点O的对称点为(-a,-b,-c)；
②点(a,b,c)关于x轴的对称点为(a,-b,-c)；
③点(a,b,c)关于y轴的对称点为(-a,b,-c)；
④点(a,b,c)关于z轴的对称点为(-a,-b,c)；
⑤点(a,b,c)关于xOy平面的对称点为(a,b,-c)；
⑥点(a,b,c)关于yOz平面的对称点为(-a,b,c)；
⑦点(a,b,c)关于zOx平面的对称点为(a,-b,c).
(2)空间点对称问题的两个技巧：
①空间点的对称问题可类比平面直角坐标系中点的对称问题，要掌握对称点的变化规律，才能准确求解.
②对称点的问题常常采用“关于谁对称，谁保持不变，其余坐标相反”这个结论.

2. (2024天津期末)已知空间向量$ \boldsymbol{a}=(1,2,-3) $，$ \boldsymbol{b}=(2,-1,1) $，则$ \boldsymbol{a}-2\boldsymbol{b}= $(A)

A.$ (-3,4,-5) $
B.$ (5,0,-5) $
C.$ (3,1,-2) $
D.$ (-1,3,-4) $

答案： 2.Aa - 2b=(1,2,-3) - 2(2,-1,1)=(1,2,-3) - (4,-2,2)=(-3,4,-5).

3. (2024江苏泰州期末)已知$ \boldsymbol{a}=(2,-1,3) $，$ \boldsymbol{b}=(-4,2,x) $，且$ \boldsymbol{a}\perp\boldsymbol{b} $，则$ x= $(D)

A.$ 2 $
B.$ 3 $
C.$ \dfrac{5}{2} $
D.$ \dfrac{10}{3} $

答案： 3.Da·b = 2×(-4)+(-1)×2 + 3x = 0，解得x = $\frac{10}{3}$.

4. (多选题，2024福建三明期末)已知正方体$ ABCD - A_1B_1C_1D_1 $的棱长为2，建立如图所示的空间直角坐标系$ D - xyz $，则(BCD)


A.点$ C_1 $的坐标为$ (2,0,2) $
B.$ \overrightarrow{C_1A}=(2,-2,-2) $
C.$ BD_1 $的中点坐标为$ (1,1,1) $
D.点$ B_1 $关于$ y $轴的对称点为$ (-2,2,-2) $

答案： 4.BCD根据题意可知点C₁的坐标为(0,2,2)，故A错误；由空间直角坐标系可知A(2,0,0)，$\overrightarrow{CA}$=(2,-2,-2)，故B正确；由空间直角坐标系可知B(2,2,0)，D₁(0,0,2)，故BD₁的中点坐标为(1,1,1)，故C正确；点B₁的坐标为(2,2,2)，关于y轴的对称点为(-2,2,-2)，故D正确.
方法总结：求空间点的坐标
(1)在空间直角坐标系中，坐标轴上的点的坐标：
x轴上的点的坐标为(x,0,0)，y轴上的点的坐标为(0,y,0)，z轴上的点的坐标为(0,0,z).
(2)在空间直角坐标系中，坐标平面上的点的坐标：
xOy平面上的点的坐标为(x,y,0)，yOz平面上的点的坐标为(0,y,z)，xOz平面上的点的坐标为(x,0,z).
(3)建立空间直角坐标系的原则：
①让尽可能多的点落在坐标轴上或坐标平面上；
②充分利用几何图形的对称性.
(4)求某点的坐标时，一般先找这一点在某个坐标轴(坐标平面)上的射影，确定射影点的坐标，再找出它在另外两个(或一个)轴上的射影，确定点的坐标.

5. (2024甘肃兰州期中)已知向量$ \overrightarrow{AB}=(1,a,-2) $，$ \overrightarrow{AC}=(-3,6,b) $，若$ A,B,C $三点共线，则$ a - b= $(A)

A.$ -8 $
B.$ -2 $
C.$ 2 $
D.$ 8 $

答案： 5.A因为A,B,C三点共线，所以$\overrightarrow{AB}$与$\overrightarrow{AC}$共线.又向量$\overrightarrow{AB}$=(1,a,-2)，$\overrightarrow{AC}$=(-3,6,b)，所以$\frac{-3}{1}=\frac{6}{a}=\frac{b}{-2}$，所以a = -2，b = 6，所以a - b = -8.

6. (2024湖南衡阳期末)已知向量$ \boldsymbol{a}=(1,0,1) $，$ \boldsymbol{b}=(x,1,2) $，且$ \boldsymbol{a}·\boldsymbol{b}=3 $，则$ \boldsymbol{a} $与$ \boldsymbol{b} $的夹角为\frac{π}{6}。

答案： 6.$\frac{π}{6}$由a·b = 3，得x + 2 = 3，解得x = 1，b=(1,1,2)，因此$\cos\langle a,b\rangle=\frac{a·b}{|a||b|}=\frac{3}{\sqrt{1 + 1 + 4}×\sqrt{1 + 1 + 4}}=\frac{\sqrt{3}}{2}$，而$\langle a,b\rangle\in[0,π]$，则$\langle a,b\rangle=\frac{π}{6}$.

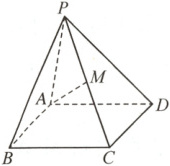
7. (2024江苏扬州阶段练习)如图，在四棱锥$ P - ABCD $中，底面$ ABCD $为菱形，$ AB = 4 $，$ \angle DAB=\dfrac{2\pi}{3} $，$ M $为棱$ PC $的中点，且$ \overrightarrow{AM}·\overrightarrow{AB}=5 $，则$ \overrightarrow{AP}·\overrightarrow{AB}= $(C)


A.$ -2 $
B.$ 0 $
C.$ 2 $
D.$ 4 $

答案：
7.C作AG⊥BC，垂足为G，以A为原点建立如图所示的空间直角坐标系，则A(0,0,0)，B(2$\sqrt{3}$,-2,0)，C(2$\sqrt{3}$,2,0).设P(x,y,z)，则M($\frac{2\sqrt{3}+x}{2}$,$\frac{2 + y}{2}$,$\frac{z}{2}$)，$\overrightarrow{AP}$=(x,y,z)，$\overrightarrow{AB}$=(2$\sqrt{3}$,-2,0)，$\overrightarrow{AM}$=($\frac{2\sqrt{3}+x}{2}$,$\frac{2 + y}{2}$,$\frac{z}{2}$).因为$\overrightarrow{AM}·\overrightarrow{AB}$ = 5，所以$\sqrt{3}$(2$\sqrt{3}$ + x) - 2 - y = 5，即$\sqrt{3}$x - y = 1，所以$\overrightarrow{AP}·\overrightarrow{AB}$ = 2$\sqrt{3}$x - 2y = 2，故C正确.
　　　　　　

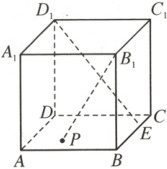
8. (2024浙江杭州期中)如图，在棱长为3的正方体$ ABCD - A_1B_1C_1D_1 $中，$ \overrightarrow{BC}=3\overrightarrow{EC} $，点$ P $在底面正方形$ ABCD $上移动(包含边界)，且满足$ B_1P\perp D_1E $，则线段$ B_1P $的长度的最大值为(B)


A.$ \dfrac{3\sqrt{190}}{10} $
B.$ \sqrt{22} $
C.$ 3\sqrt{2} $
D.$ \dfrac{\sqrt{166}}{3} $

答案：
8.B以{DA,DC,DD₁}为正交基底，建立如图所示的空间直角坐标系D - xyz，则D₁(0,0,3)，E(1,3,0)，B₁(3,3,3).设P(x,y,0)(x,y∈[0,3])，所以$\overrightarrow{B₁P}$=(x - 3,y - 3,-3)，$\overrightarrow{D₁E}$=(1,3,-3)，所以$\overrightarrow{B₁P}·\overrightarrow{D₁E}$ = x + 3y - 3 = 0，即x = 3 - 3y，所以0≤3 - 3y≤3，即y∈[0,1]，而$|\overrightarrow{B₁P}|=\sqrt{(x - 3)^2+(y - 3)^2+9}=\sqrt{10y^2 - 6y + 18}$.由二次函数的单调性可知t = 10y² - 6y + 18 = 10(y - $\frac{3}{10}$)² + 18 - $\frac{9}{10}$，当y = 1时，t_max = 22，则$B₁P_max=\sqrt{22}$.
　　　　　　　　　　　　

9. (多选题，2024福建泉州期中)在菱形纸片$ ABCD $中，$ E,F $分别为$ AD,BC $的中点，$ O $是菱形$ ABCD $的中心，$ AB = 2 $，$ \angle ABC=\dfrac{2\pi}{3} $，将菱形纸片$ ABCD $沿对角线$ AC $折成直二面角，以$ O $为原点，$ \{ \overrightarrow{OB},\overrightarrow{OC},\overrightarrow{OD} \} $为正交基底，建立如图所示的空间直角坐标系，则(ACD)


A.$ E\left(0,-\dfrac{\sqrt{3}}{2},\dfrac{1}{2}\right) $
B.$ F\left(\dfrac{\sqrt{3}}{2},\dfrac{1}{2},0\right) $
C.$ \overrightarrow{EF}=\left(\dfrac{1}{2},\sqrt{3},-\dfrac{1}{2}\right) $
D.$ \cos\angle EOF=-\dfrac{3}{4} $

答案： 9.ACD由题意可知AC = 2$\sqrt{3}$，BD = 2，所以A(0,-$\sqrt{3}$,0)，C(0,$\sqrt{3}$,0)，B(1,0,0)，D(0,0,1)，所以E(0,-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)，F($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,0)，则$\overrightarrow{OE}$=(0,-$\frac{\sqrt{3}}{2}$,$\frac{1}{2}$)，$\overrightarrow{OF}$=($\frac{1}{2}$,$\frac{\sqrt{3}}{2}$,0)，$\overrightarrow{EF}$=($\frac{1}{2}$,$\sqrt{3}$,-$\frac{1}{2}$)，易知∠EOF为钝角，所以$\cos∠EOF=-|\cos\langle\overrightarrow{OE},\overrightarrow{OF}\rangle|=-\frac{|\overrightarrow{OE}·\overrightarrow{OF}|}{|\overrightarrow{OE}||\overrightarrow{OF}|}=-\frac{3}{4}$.综上，A,C,D正确，B错误.