《2025年小题狂做高中数学选择性必修第二册苏教版》

1. 下列问题是排列问题的是 (B)

A.从 8 名同学中选取 2 名去参加知识竞赛，共有多少种不同的选取方法
B.会场中有 30 个座位，任选 3 个安排 3 位客人入座，有多少种坐法
C.平面上有 5 个点，任意三点不共线，这 5 个点最多可确定多少条直线
D.从 1,2,3,4 四个数字中，任选两个相乘，其结果共有多少种

答案： 1. B 对于A，8名同学中选取2名，不涉及顺序问题，不是排列问题，故A错误；对于B，“入座问题”与顺序有关，是排列问题，故B正确；对于C，确定直线的两点不涉及顺序问题，不是排列问题，故C错误；对于D，4个数字中任取2个相乘，根据乘法交换律知，结果不涉及顺序问题，不是排列问题，故D错误.

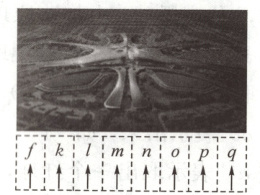
2. (2023 河南期中)北京大兴国际机场拥有世界上最大的单一航站楼，并拥有机器人自动泊车系统，解决了停车满、找车难的问题.现有 5 辆车停放在 8 个并排的泊车位上，要求停放的车辆相邻，箭头表示车头朝向，则不同的泊车方案数有 (C)


A.120
B.240
C.480
D.960

答案： 2. C 从8个车位里选择5个相邻的车位，共有4种方式，即fklmn，klmno，lmnop，mnopq，选一种方式将5辆车相邻停放，有$A_5^5=120$方式，则不同的泊车方案有$4 × 120 = 480$种.

3. 某公司为庆祝年利润实现目标，计划举行答谢联欢会，原定表演 6 个节目，已排好节目单，开演前又临时增加了 2 个互动节目.如果保持原节目的顺序不变，那么不同排法的种数为 (B)

A.42
B.56
C.30
D.72

答案： 3. B 增加2个互动节目后，一共有8个节目，这8个节目的不同排法有$A_8^8$种，而原有的6个节目对应的不同排法共有$A_6^6$种，所以不同的排法有$\frac{A_8^8}{A_6^6}=56$种.
方法总结 对于定序的问题，只需要应用倍缩法，将顺序去除即可.

4. (多选题)下列等式成立的是 (BCD)

A.$\mathrm{A}_n^m=\frac{n!}{m!}$
B.$(n+1)\mathrm{A}_n^m=\mathrm{A}_{n+1}^{m+1}$
C.$\mathrm{A}_{n+1}^{n+1}-\mathrm{A}_n^n=n^2\mathrm{A}_{n-1}^{n-1}$
D.$n\mathrm{A}_{n-1}^{n-1}=n!$

答案： 4. BCD $A_n^m=\frac{n!}{(n-m)!}$，故A错误；$(n + 1)A_n^m=(n + 1)· \frac{n!}{(n-m)!}=\frac{(n+1)!}{(n-m)!}=A_{n+1}^{m+1}=\frac{(n+1)!}{(n+1-m-1)!}=\frac{(n+1)!}{(n-m)!}$，故B正确；$A_{n+1}^{n+1}-A_n^n=(n+1)!-n!=n!·(n+1-1)=n· n!$，$n^2A_{n-1}^{n-1}=n^2(n-1)!=n· n!$，故C正确；$nA_{n-1}^{n-1}=n(n-1)!=n!$，故D正确.

5. (2024 江苏南京阶段练习)一条铁路线原有 $n$ 个车站，为了适应客运需要，新增加了 2 个车站，客运车票增加了 58 种，则原有车站14 个.

答案： 5. 14 由题意可得，$A_{n+2}^2 - A_n^2 = 58$，即$(n+2)(n+1)-n(n-1)=58$，解得$n=14$.

6. (2024 黑龙江哈尔滨期末)初等数论中的四平方和定理最早由欧拉提出，后被拉格朗日等数学家证明.四平方和定理的内容是：任意正整数都可以表示为四个自然数的平方和，例如正整数 $6=2^2+1^2+1^2+0^2$.设 $38=a^2+b^2+c^2+d^2$，其中 $a,b,c,d$ 均为自然数，则满足条件的有序数组 $(a,b,c,d)$ 的个数为48(用数字作答).

答案： 6. 48 依题意，$a,b,c,d$均为不超过6的自然数，最大数为6的情况：$38 = 6^2 + 1^2 + 1^2 + 0^2$，此时共有$A_2^2 = 12$个有序数组.最大数为5的情况：$38 = 5^2 + 3^2 + 2^2 + 0^2$，此时共有$A_4^4 = 24$个有序数组.最大数为4的情况：$38 = 4^2 + 3^2 + 3^2 + 2^2$，此时共有$\frac{A_4^4}{A_2^2A_2^2}=12$个有序数组.当最大数为3时，$3^2 + 3^2 + 3^2 + 3^2 ＜ 38$，不满足题意.由分类计数原理，满足条件的有序数组$(a,b,c,d)$的个数是$12 + 24 + 12 = 48$.

7. (2025 江西开学考试)甲、乙等四个人一起随机手牵手围成一圈做游戏，则甲与乙牵手的概率是 (D)

A.$\frac{1}{2}$
B.$\frac{1}{3}$
C.$\frac{1}{4}$
D.$\frac{2}{3}$

答案： 7. D 以甲为中心，其他三人的位置是甲的左边、右边、对面，共有$A_3^3$种情况，其中乙在甲左边或右边，即甲与乙能牵手有$2A_2^2$种情况，所以所求概率$P=\frac{2A_2^2}{A_3^3}=\frac{2}{3}$.

8. 若 $M=\mathrm{A}_1^1+\mathrm{A}_2^2+\mathrm{A}_3^3+·s+\mathrm{A}_{2023}^{2023}$，则 $M$ 的个位数字是 (A)

A.3
B.8
C.0
D.5

答案： 8. A 因为当$n \geq 5$时，$A_n^n = 1 × 2 × 3 × 4 × 5 × ·s × n$，所以当$n \geq 5$时，$A_n^n$的个位数字为0. 又$A_5^5 + A_5^2 + A_5^3 + A_5^4 = 1 + 2 + 6 + 24 = 33$，所以M的个位数字为3.

9. (多选题)由 0,1,2,3,4,5,6,7,8,9 这十个数字组成无重复数字的五位数，且 1 不能在个位，则关于这样的五位数的个数，下列表示正确的有 (BCD)

A.$(\mathrm{A}_9^1)^2\mathrm{A}_8^3$
B.$\mathrm{A}_9^4+(\mathrm{A}_8^1)^2\mathrm{A}_8^3$
C.$\mathrm{A}_{10}^5-2\mathrm{A}_9^4+\mathrm{A}_8^3$
D.$\mathrm{A}_9^4+\mathrm{A}_8^1\mathrm{A}_8^1\mathrm{A}_8^3+\mathrm{A}_8^1\mathrm{A}_8^4$

答案： 9. BCD （排除法）从十个数字中任选五个进行排列，有$A_{10}^5$个五位数，1在个位和0在第一位的共有$2A_9^4$个五位数，0在第一位且1在个位的有$A_8^3$个五位数，则符合题意的五位数共有$A_{10}^5 - 2A_9^4 + A_8^3$个，故C正确.（讨论法）若有1，且1在第一位，共有$A_9^4$个五位数；1在第二、三、四位，共有$A_8^1A_8A_3^3$个五位数.若没有1，第一位有$A_8^1$种选法，剩下的四位有$A_8^4$种选法，共有$A_8^1A_8^4$个五位数.故符合题意的有$A_9^4 + A_8^1A_8A_3^3 + A_8^1A_8^4$个五位数，故D正确. 又$A_8^1A_8A_3^3 + A_8^1A_8^4 = A_8^1(A_8A_3^3 + A_8^4) = A_8^1A_8^3 × 8 = (A_8^1)^2A_8^3$，故B正确.
方法总结 对某些元素“在”或“不在”某些位置上、某些位置上“排”或“不排”，常使用“优先法”或“排除法”.

10. (多选题，2024 山东期中)已知 4 位身高各不相同的男生和 3 位女生站成一排，则 (ABD)

A.共有 $\mathrm{A}_7^7$ 种不同的排法
B.若女生互不相邻，共有 1440 种不同的排法
C.若男生站一起、女生站一起，共有 144 种不同的排法
D.若男生从左到右身高逐渐增加，共有 210 种不同的排法

答案： 10. ABD 对于A，7个人全排列，共有$A_7^7$种不同的排法，故A正确；对于B，先排男生，再把女生插入空隙，有$A_4^4A_3^3 = 1440$种，故B正确；对于C，分别把男生、女生视为一个整体排列，共有$A_4^4A_3^3 = 288$种，故C错误；对于D，7个人全排列，而男生的排列方法只占$\frac{1}{A_4^4}$，共有$\frac{A_7^7}{A_4^4}=210$种，故D正确.
方法总结 对于某些元素“相邻”的问题，常常采用捆绑法；对于某些元素彼此“不相邻（相间）”的问题，常常采用插空法.