2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第73页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
6. 某校为了弘扬与传承中华优秀传统文化,特地举办了“国学经典”知识竞赛活动,规则如下:①单选题答对得20分,答错得0分;②多选题答对得30分,选对但不全得10分,有错选得0分;③每名竞赛参与者答题3道.学校设计了两种答题方案.方案一:全部回答单选题.方案二:先回答一道多选题,再回答单选题.现已知某学生单选题答对的概率为0.8,多选题全对的概率为0.4,选对但不全的概率为0.3,则能使得该学生的得分更高,应该选择(
A.方案一
B.方案二
C.两种方案都一样
D.无法确定
A
)A.方案一
B.方案二
C.两种方案都一样
D.无法确定
答案:
6. A 若该学生选择方案一,设得分为 $X$,则 $X$ 的取值可能是 0,20,40,60,可得 $P(X = 0)=C_3^0 × 0.8^0 × 0.2^3 = 0.008$,$P(X = 20)=C_3^1 × 0.8 × 0.2^2 = 0.096$,$P(X = 40)=C_3^2 × 0.8^2 × 0.2 = 0.384$,$P(X = 60)=C_3^3 × 0.8^3 = 0.512$,则 $X$ 的分布列为
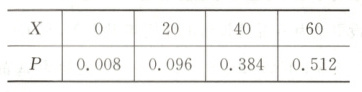
所以期望为 $E(X)=0 + 20 × 0.096 + 40 × 0.384 + 60 × 0.512 = 48$. 若该学生选择方案二,记得分为 $Y$,则 $Y$ 的取值可能为 0,10,20,30,40,50,70,可得 $P(Y = 0)=0.3 × 0.2 × 0.2 = 0.012$,$P(Y = 10)=0.3 × 0.2 × 0.2 = 0.012$,$P(Y = 20)=0.3 × 0.8 × 0.2 × 2 = 0.096$,$P(Y = 30)=0.3 × 0.8 × 0.2 × 2 + 0.4 × 0.2 × 0.2 = 0.112$,$P(Y = 40)=0.3 × 0.8 × 0.8 = 0.192$,$P(Y = 50)=0.3 × 0.8 × 0.8 + 0.4 × 0.8 × 0.2 × 2 = 0.32$,$P(Y = 70)=0.4 × 0.8 × 0.8 = 0.256$,则 $Y$ 的分布列为

所以期望为 $E(Y)=0 × 0.012 + 10 × 0.012 + 20 × 0.096 + 30 × 0.112 + 40 × 0.192 + 50 × 0.32 + 70 × 0.256 = 47$. 因为 $E(X)>E(Y)$,所以选择方案一,能使得该生的得分更高.
6. A 若该学生选择方案一,设得分为 $X$,则 $X$ 的取值可能是 0,20,40,60,可得 $P(X = 0)=C_3^0 × 0.8^0 × 0.2^3 = 0.008$,$P(X = 20)=C_3^1 × 0.8 × 0.2^2 = 0.096$,$P(X = 40)=C_3^2 × 0.8^2 × 0.2 = 0.384$,$P(X = 60)=C_3^3 × 0.8^3 = 0.512$,则 $X$ 的分布列为

所以期望为 $E(X)=0 + 20 × 0.096 + 40 × 0.384 + 60 × 0.512 = 48$. 若该学生选择方案二,记得分为 $Y$,则 $Y$ 的取值可能为 0,10,20,30,40,50,70,可得 $P(Y = 0)=0.3 × 0.2 × 0.2 = 0.012$,$P(Y = 10)=0.3 × 0.2 × 0.2 = 0.012$,$P(Y = 20)=0.3 × 0.8 × 0.2 × 2 = 0.096$,$P(Y = 30)=0.3 × 0.8 × 0.2 × 2 + 0.4 × 0.2 × 0.2 = 0.112$,$P(Y = 40)=0.3 × 0.8 × 0.8 = 0.192$,$P(Y = 50)=0.3 × 0.8 × 0.8 + 0.4 × 0.8 × 0.2 × 2 = 0.32$,$P(Y = 70)=0.4 × 0.8 × 0.8 = 0.256$,则 $Y$ 的分布列为

所以期望为 $E(Y)=0 × 0.012 + 10 × 0.012 + 20 × 0.096 + 30 × 0.112 + 40 × 0.192 + 50 × 0.32 + 70 × 0.256 = 47$. 因为 $E(X)>E(Y)$,所以选择方案一,能使得该生的得分更高.
7. (多选题,2023湖南长郡中学月考)小张上班从家到公司开车有两条线路,所需时间(分钟)随交通堵塞状况有所变化,其概率分布如下表所示.
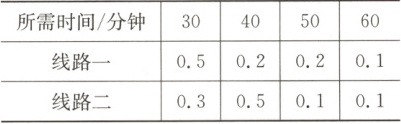
则下列说法正确的是(
A.任选一条线路,“所需时间小于50分钟”与“所需时间为60分钟”是对立事件
B.从所需的平均时间看,线路一比线路二更节省时间
C.如果要求在45分钟以内从家赶到公司,那么小张应该走线路一
D.若小张上下班走不同线路,则所需时间之和大于100分钟的概率为0.04

则下列说法正确的是(
BD
)A.任选一条线路,“所需时间小于50分钟”与“所需时间为60分钟”是对立事件
B.从所需的平均时间看,线路一比线路二更节省时间
C.如果要求在45分钟以内从家赶到公司,那么小张应该走线路一
D.若小张上下班走不同线路,则所需时间之和大于100分钟的概率为0.04
答案:
7. BD 对于选项 A,“所需时间小于 50 分钟”与“所需时间为 60 分钟”是互斥而不对立事件,故选项 A 错误;对于选项 B,线路一所需的平均时间为 $30 × 0.5 + 40 × 0.2 + 50 × 0.2 + 60 × 0.1 = 39$(分钟),线路二所需的平均时间为 $30 × 0.3 + 40 × 0.5 + 50 × 0.1 + 60 × 0.1 = 40$(分钟),所以线路一比线路二更节省时间,故选项 B 正确;对于选项 C,线路一所需时间小于 45 分钟的概率为 0.7,线路二所需时间小于 45 分钟的概率为 0.8,小张应该选线路二,故选项 C 错误;对于选项 D,若所需时间之和大于 100 分钟,则线路一、线路二的时间可以为(50,60),(60,50)和(60,60)三种情况,概率为 $0.2 × 0.1 + 0.1 × 0.1 + 0.1 × 0.1 = 0.04$,故选项 D 正确.
8. (多选题,2023江苏南通海门中学期中)已知投资A,B两种项目获得的收益分别为$X$,$Y$,其分布列如下表,则(

A.$m+n=0.5$
B.$E(2X+1)=4$
C.投资两种项目的收益期望一样多
D.投资A项目的风险比B项目高
ACD
)
A.$m+n=0.5$
B.$E(2X+1)=4$
C.投资两种项目的收益期望一样多
D.投资A项目的风险比B项目高
答案:
8. ACD 依题意可得 $0.2 + m + 0.6 = 1$,所以 $m = 0.2$,$0.3 + 0.4 + n = 1$,所以 $n = 0.3$,所以 $m + n = 0.5$,故 A 正确;$E(X)= - 1 × 0.2 + 0 × 0.2 + 2 × 0.6 = 1$,则 $E(2X + 1)=2E(X)+1 = 3$,故 B 错误;$E(Y)=0 × 0.3 + 1 × 0.4 + 2 × 0.3 = 1$,所以 $E(X)=E(Y)$,故 C 正确;因为 $D(X)=(-1 - 1)^2 × 0.2 + (0 - 1)^2 × 0.2 + (2 - 1)^2 × 0.6 = 1.6$,$D(Y)=(0 - 1)^2 × 0.3 + (1 - 1)^2 × 0.4 + (2 - 1)^2 × 0.3 = 0.6$,即 $D(X)>D(Y)$,所以投资 A 项目的风险比 B 项目高,故 D 正确.
9. (多选题,2023江苏盐城期中)已知8只小白鼠中有1只患有某种疾病,需要通过血液化验来确定患这种病的小白鼠,血液化验结果呈阳性的为患病小白鼠,下面是两种化验方案.方案甲:将8只小白鼠的血液逐个化验,直到查出患病小白鼠为止.方案乙:先取4只小白鼠的血液混在一起化验,若呈阳性,则对这4只小白鼠的血液再逐个化验,直到查出患病小白鼠;若不呈阳性,则对剩下的4只小白鼠再逐个化验,直到查出患病小白鼠.则下列结论正确的是(
A.若采用方案甲,则化验次数为2的概率为$\frac{1}{8}$
B.若采用方案乙,则化验次数为3的概率为$\frac{1}{8}$
C.若采用方案甲,则平均化验次数为4
D.若平均化验次数少的方案好,则方案乙比方案甲好
AD
)A.若采用方案甲,则化验次数为2的概率为$\frac{1}{8}$
B.若采用方案乙,则化验次数为3的概率为$\frac{1}{8}$
C.若采用方案甲,则平均化验次数为4
D.若平均化验次数少的方案好,则方案乙比方案甲好
答案:
9. AD 若采用方案甲,设化验次数为 $X$,则 $X$ 的可能取值为 1,2,3,4,5,6,7,所以 $P(X = 1)=\frac{1}{8}$,$P(X = 2)=\frac{7}{8} × \frac{1}{7}=\frac{1}{8}$,故 A 正确. 若采用方案乙,设化验次数为 $Y$,当 $Y = 3$ 时,有两种情况:①头 4 只均为阴性,则 $P_1=\frac{C_7^4}{C_8^4} × \frac{3}{4} × \frac{1}{3}=\frac{1}{8}$;②头 4 只有阳性,则 $P_2=\frac{C_7^3 C_1^1}{C_8^4} × \frac{3}{4} × \frac{1}{3}=\frac{1}{8}$,所以化验次数为 3 的概率为 $P(Y = 3)=\frac{1}{8} + \frac{1}{8}=\frac{1}{4}$,故 B 错误. 若采用方案甲,则 $P(X = 3)=P(X = 4)=P(X = 5)=P(X = 6)=\frac{1}{8}$,$P(X = 7)=1 - \frac{6}{8}=\frac{1}{4}$,所以 $E(X)=(1 + 2 + 3 + 4 + 5 + 6) × \frac{1}{8} + 7 × \frac{1}{4}=\frac{35}{8}$,故 C 错误. 若采用方案乙,$Y$ 可取 2,3,4,$P(Y = 2)=\frac{C_8^4}{C_8^4} × \frac{1}{4} + \frac{C_7^3 C_1^1}{C_8^4} × \frac{1}{4} × \frac{1}{4}=\frac{1}{4}$,$P(Y = 3)=\frac{1}{4}$,$P(Y = 4)=1 - \frac{1}{4} × 2=\frac{1}{2}$,所以 $E(Y)=2 × \frac{1}{4} + 3 × \frac{1}{4} + 4 × \frac{1}{2}=\frac{13}{4}$,因为 $E(X)>E(Y)$,所以方案乙比方案甲好,故 D 正确.
10. (2024河北邢台期末)某校组织“中国诗词”竞赛,在“风险答题”的环节中,共为选手准备了A,B,C三类不同的题目,选手每答对一个A类、B类或C类题目,将分别得到300分,200分,100分,但如果答错,则相应要扣去300分,200分,100分,根据平时训练经验,选手甲答对A类、B类、C类题目的概率分别为0.6,0.75,0.85.若要每一次答题的均分更大一些,则选手甲选择的题目类型应为
B
(填A,B或C).
答案:
10. B 选手甲选择 A 类题目,得分的均值为 $0.6 × 300 + 0.4 × (-300)=60$,选手甲选择 B 类题目,得分的均值为 $0.75 × 200 + 0.25 × (-200)=100$,选手甲选择 C 类题目,得分的均值为 $0.85 × 100 + 0.15 × (-100)=70$,所以若要每一次答题的均分更大一些,则选手甲选择的题目类型应为 B.
11. (2024陕西咸阳阶段调研)有30件产品,其中有10件次品,从中不放回地抽取10件产品,最可能抽到的次品数是
3
.
答案:
11. 3 由题意,有 30 件产品,其中有 10 件次品,从中不放回地抽取 10 产品,则抽出的次品数 $X$ 服从超几何分布,设最可能抽到的次品数为 $k$,则$\begin{cases} \frac{(C_{k}^{k} C_{20}^{10 - k})}{(C_{30}^{10})} \geqslant \frac{(C_{k - 1}^{k - 1} C_{20}^{11 - k})}{(C_{30}^{10})}, \\ \frac{(C_{k}^{k} C_{20}^{10 - k})}{(C_{30}^{10})} \geqslant \frac{(C_{k + 1}^{k + 1} C_{20}^{9 - k})}{(C_{30}^{10})}. \end{cases}$ 整理得 $\frac{89}{32} \leqslant k \leqslant \frac{121}{32}$. 又 $k \in N^*$,所以 $k = 3$,故最可能抽到的次品数是 3.
12. (2024上海松江二中月考)王先生每天8点上班,他通常开私家车加步行或乘坐地铁加步行.私家车路程近一些,但路上经常拥堵,所需时间(单位:分钟)服从正态分布$N(38,7^{2})$,从停车场步行到单位要6分钟.王先生从家到地铁站需要步行5分钟,乘坐地铁畅通,但路线较长,所需时间(单位:分钟)服从正态分布$N(44,2^{2})$,下地铁后从地铁站步行到单位要5分钟.从统计角度出发,关于两种上班方式,下列说法正确的个数是
①若7:00出门,则王先生开私家车上班不会迟到;
②若7:02出门,则王先生开私家车上班不迟到的可能性更大;
③若7:06出门,则王先生乘坐地铁上班不迟到的可能性更大;
④若7:12出门,则王先生乘坐地铁上班几乎不可能不迟到.
参考数据:若$Z\sim N(\mu,\sigma^{2})$,则$P(\vert Z-\mu\vert\lt\sigma)\approx0.6826$,$P(\vert Z-\mu\vert\lt2\sigma)\approx0.9544$,$P(\vert Z-\mu\vert\lt3\sigma)\approx0.9974$.
1
.①若7:00出门,则王先生开私家车上班不会迟到;
②若7:02出门,则王先生开私家车上班不迟到的可能性更大;
③若7:06出门,则王先生乘坐地铁上班不迟到的可能性更大;
④若7:12出门,则王先生乘坐地铁上班几乎不可能不迟到.
参考数据:若$Z\sim N(\mu,\sigma^{2})$,则$P(\vert Z-\mu\vert\lt\sigma)\approx0.6826$,$P(\vert Z-\mu\vert\lt2\sigma)\approx0.9544$,$P(\vert Z-\mu\vert\lt3\sigma)\approx0.9974$.
答案:
12. 1 对于①,由题得,当满足 $P(Z \geqslant 59)=1 - P(17 < Z < 59) \approx \frac{1 - 0.9974}{2}=0.0013$ 时,概率小也可能发生,加上步行 6 分钟,就迟到了,所以①错误. 对于②,若 7:02 出门,分 2 种情况,若开私家车,当满足 $P(Z \leqslant 52)=1 - P(24 < Z < 52)+P(24 < Z < 52)=0.9772$ 时,不会迟到;若乘坐地铁,当满足 $P(Z \leqslant 48)=\frac{1 - P(40 < Z < 48)}{2}=0.5$ 时,不会迟到. 此时两种方式,不迟到的概率相当,所以②错误. 对于③,若 7:06 出门,分 2 种情况,若开私家车,当满足 $P(Z \leqslant 48)>P(Z \leqslant 45)=\frac{1 - P(31 < Z < 45)}{2}+P(31 < Z < 45)=0.8413$ 时,不会迟到;若乘坐地铁,当满足 $P(Z \leqslant 44)=\frac{1}{2}=0.5$ 时,不会迟到. 此时两种方式,显然开私家车不迟到的可能性更大,所以③错误. 对于④,若 7:12 出门,乘坐地铁上班,当满足 $P(Z \leqslant 38)=\frac{1 - P(38 < Z < 50)}{2}=0.0013$ 时,不会迟到,此时不迟到的可能性极小,故乘坐地铁上班几乎不可能不迟到,所以④正确.
查看更多完整答案,请扫码查看


