2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第15页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
8. (2024河北邢台二模)在直三棱柱$ABC - A_{1}B_{1}C_{1}$中,$\angle BAC = \dfrac{\pi}{2}$,$AB = AC = 2$,$AA_{1} = 3$。
(1) 如图1,$E$为$C_{1}A$上的一动点,$F$为棱$BC$上的一动点,且$\dfrac{AE}{AC_{1}} = \dfrac{CF}{BC}$,求线段$EF$长的最小值。
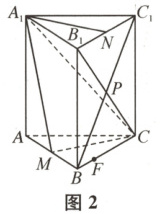
(2) 如图2,$M$是棱$AB$的中点,$N$是棱$B_{1}C_{1}$的中点,$P$是$BC_{1}$与$B_{1}C$的交点。线段$A_{1}N$上是否存在点$Q$,使得$PQ//$平面$A_{1}CM$?若存在,请确定点$Q$的位置;若不存在,请说明理由。

(1) 如图1,$E$为$C_{1}A$上的一动点,$F$为棱$BC$上的一动点,且$\dfrac{AE}{AC_{1}} = \dfrac{CF}{BC}$,求线段$EF$长的最小值。
(2) 如图2,$M$是棱$AB$的中点,$N$是棱$B_{1}C_{1}$的中点,$P$是$BC_{1}$与$B_{1}C$的交点。线段$A_{1}N$上是否存在点$Q$,使得$PQ//$平面$A_{1}CM$?若存在,请确定点$Q$的位置;若不存在,请说明理由。


答案:
8. 解:
(1) 如图,以$\{\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AA_{1}}\}$为正交基底,建立如图所示的空间直角坐标系$A - xyz$,设$AE = \lambda\overrightarrow{AC_{1}}$,$0 \leq \lambda \leq 1$,则$CF = \lambda\overrightarrow{CB}$,$A(0,0,0)$,$B(2,0,0)$,$C(0,2,0)$,$C_{1}(0,2,3)$,故$\overrightarrow{EF} = \overrightarrow{EA} + \overrightarrow{AC} + \overrightarrow{CF} = -\lambda\overrightarrow{AC_{1}} + \overrightarrow{AC} + \lambda\overrightarrow{CB} = -\lambda(0,2,3) + (0,2,0) + \lambda(2,-2,0) = (2\lambda, 2 - 4\lambda, -3\lambda)$,所以$|\overrightarrow{EF}| = \sqrt{4\lambda^{2} + (2 - 4\lambda)^{2} + 9\lambda^{2}} = \sqrt{29\lambda^{2} - 16\lambda + 4}$,当$\lambda = \frac{8}{29}$时,$|\overrightarrow{EF}|$取得最小值$\frac{2\sqrt{377}}{29}$,所以线段$EF$长的最小值为$\frac{2\sqrt{377}}{29}$。
(2) 假设存在。设$\overrightarrow{A_{1}Q} = t\overrightarrow{A_{1}N}$,$0 \leq t \leq 1$。$C(0,2,0)$,$M(1,0,0)$,$P(1,1,\frac{3}{2})$,$N(1,1,3)$,$A_{1}(0,0,3)$,故$\overrightarrow{A_{1}M} = (1,0,-3)$,$\overrightarrow{A_{1}C} = (0,2,-3)$,$\overrightarrow{PA_{1}} = (-1,-1,\frac{3}{2})$,$\overrightarrow{A_{1}N} = (1,1,0)$,所以$\overrightarrow{PQ} = \overrightarrow{PA_{1}} + \overrightarrow{A_{1}Q} = \overrightarrow{PA_{1}} + t\overrightarrow{A_{1}N} = (-1,-1,\frac{3}{2}) + t(1,1,0) = (t - 1,t - 1,\frac{3}{2})$。设平面$A_{1}CM$的法向量为$\mathbf{n} = (x, y, z)$,则$\begin{cases}\mathbf{n} · \overrightarrow{A_{1}M} = x - 3z = 0 \\\mathbf{n} · \overrightarrow{A_{1}C} = 2y - 3z = 0\end{cases}$,令$x = 6$,则$z = 2$,$y = 3$,所以$\mathbf{n} = (6,3,2)$。因为$\overrightarrow{PQ} //$平面$A_{1}CM$,所以$\mathbf{n} \perp \overrightarrow{PQ}$,则$\mathbf{n} · \overrightarrow{PQ} = 6(t - 1) + 3(t - 1) + 3 = 0$,解得$t = \frac{2}{3}$,所以线段$A_{1}N$上存在点$Q$,在靠近点$N$的三等分点处,使得$PQ //$平面$A_{1}CM$。

8. 解:
(1) 如图,以$\{\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AA_{1}}\}$为正交基底,建立如图所示的空间直角坐标系$A - xyz$,设$AE = \lambda\overrightarrow{AC_{1}}$,$0 \leq \lambda \leq 1$,则$CF = \lambda\overrightarrow{CB}$,$A(0,0,0)$,$B(2,0,0)$,$C(0,2,0)$,$C_{1}(0,2,3)$,故$\overrightarrow{EF} = \overrightarrow{EA} + \overrightarrow{AC} + \overrightarrow{CF} = -\lambda\overrightarrow{AC_{1}} + \overrightarrow{AC} + \lambda\overrightarrow{CB} = -\lambda(0,2,3) + (0,2,0) + \lambda(2,-2,0) = (2\lambda, 2 - 4\lambda, -3\lambda)$,所以$|\overrightarrow{EF}| = \sqrt{4\lambda^{2} + (2 - 4\lambda)^{2} + 9\lambda^{2}} = \sqrt{29\lambda^{2} - 16\lambda + 4}$,当$\lambda = \frac{8}{29}$时,$|\overrightarrow{EF}|$取得最小值$\frac{2\sqrt{377}}{29}$,所以线段$EF$长的最小值为$\frac{2\sqrt{377}}{29}$。
(2) 假设存在。设$\overrightarrow{A_{1}Q} = t\overrightarrow{A_{1}N}$,$0 \leq t \leq 1$。$C(0,2,0)$,$M(1,0,0)$,$P(1,1,\frac{3}{2})$,$N(1,1,3)$,$A_{1}(0,0,3)$,故$\overrightarrow{A_{1}M} = (1,0,-3)$,$\overrightarrow{A_{1}C} = (0,2,-3)$,$\overrightarrow{PA_{1}} = (-1,-1,\frac{3}{2})$,$\overrightarrow{A_{1}N} = (1,1,0)$,所以$\overrightarrow{PQ} = \overrightarrow{PA_{1}} + \overrightarrow{A_{1}Q} = \overrightarrow{PA_{1}} + t\overrightarrow{A_{1}N} = (-1,-1,\frac{3}{2}) + t(1,1,0) = (t - 1,t - 1,\frac{3}{2})$。设平面$A_{1}CM$的法向量为$\mathbf{n} = (x, y, z)$,则$\begin{cases}\mathbf{n} · \overrightarrow{A_{1}M} = x - 3z = 0 \\\mathbf{n} · \overrightarrow{A_{1}C} = 2y - 3z = 0\end{cases}$,令$x = 6$,则$z = 2$,$y = 3$,所以$\mathbf{n} = (6,3,2)$。因为$\overrightarrow{PQ} //$平面$A_{1}CM$,所以$\mathbf{n} \perp \overrightarrow{PQ}$,则$\mathbf{n} · \overrightarrow{PQ} = 6(t - 1) + 3(t - 1) + 3 = 0$,解得$t = \frac{2}{3}$,所以线段$A_{1}N$上存在点$Q$,在靠近点$N$的三等分点处,使得$PQ //$平面$A_{1}CM$。

9. (2024上海浦东期末)已知棱长均为$1$的正$n$棱柱有$2n$个顶点,从中任取两个顶点作为向量$\boldsymbol{a}$的起点与终点,设底面的一条棱为$AB$。若集合$A_{n} = \{x\mid x = \boldsymbol{a}·\overrightarrow{AB}\}$,则当$A_{n}$中的元素个数最少时,$n$的值为(
A.$3$
B.$4$
C.$6$
D.$8$
B
)A.$3$
B.$4$
C.$6$
D.$8$
答案:
9. B 如图,设$AB$所在的直线为$x$轴,过点$A$且与$AB$垂直的直线为$y$轴,过点$A$且与平面$xAy$垂直的直线为$z$轴,建立如图所示的空间直角坐标系$A - xyz$,
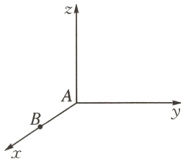
则$A(0,0,0)$,$B(1,0,0)$,得$\overrightarrow{AB} = (1,0,0)$,设$\mathbf{a} = (x, y, z)$,则$\mathbf{a} · \overrightarrow{AB} = (x, y, z) · (1,0,0) = x$。因为该几何体为正$n$棱柱,所以上底面与下底面对应各顶点的横坐标相等。当$n = 3$时,该几何体为正三棱柱,作出其底面$ABC$的示意图,如图:
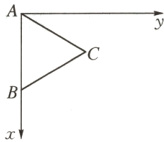
则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = \frac{1}{2}$,所以$x = 0$或$\pm \frac{1}{2}$或$\pm 1$,即$A_{3} = \{0, \pm \frac{1}{2}, \pm 1\}$,共有$5$个元素。当$n = 4$时,该几何体为正方体,作出其底面$ABCD$的示意图,如图:
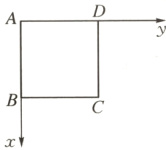
则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = 1$,$x_{D} = 0$,所以$x = 0$或$\pm 1$,即$A_{4} = \{0, \pm 1\}$,共有$3$个元素。当$n = 6$时,该几何体为正六棱柱,作出其底面$ABCDEF$的示意图,如图:
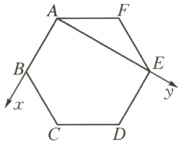
则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = \frac{3}{2}$,$x_{D} = 1$,$x_{E} = 0$,$x_{F} = -\frac{1}{2}$,所以$x = 0$或$\pm \frac{1}{2}$或$\pm 1$或$\pm \frac{3}{2}$或$\pm 2$,即$A_{6} = \{0, \pm \frac{1}{2}, \pm 1, \pm \frac{3}{2}, \pm 2\}$,共有$9$个元素。当$n = 8$时,该几何体为正八棱柱,作出其底面$ABCDEFGH$的示意图,如图:
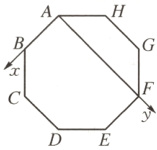
则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = 1 + \frac{\sqrt{2}}{2}$,$x_{D} = 1 + \frac{\sqrt{2}}{2}$,$x_{E} = 1$,$x_{F} = 0$,$x_{G} = -\frac{\sqrt{2}}{2}$,$x_{H} = -\frac{\sqrt{2}}{2}$,所以$x = 0$或$\pm \frac{\sqrt{2}}{2}$或$\pm 1$或$\pm (1 + \frac{\sqrt{2}}{2})$或$\pm (1 + \sqrt{2})$,即$A_{8} = \{0, \pm \frac{\sqrt{2}}{2}, \pm 1, \pm (1 + \frac{\sqrt{2}}{2}), \pm (1 + \sqrt{2})\}$,共有$9$个元素。综上,当$n = 4$时,$A_{n}$中的元素个数最少。
9. B 如图,设$AB$所在的直线为$x$轴,过点$A$且与$AB$垂直的直线为$y$轴,过点$A$且与平面$xAy$垂直的直线为$z$轴,建立如图所示的空间直角坐标系$A - xyz$,

则$A(0,0,0)$,$B(1,0,0)$,得$\overrightarrow{AB} = (1,0,0)$,设$\mathbf{a} = (x, y, z)$,则$\mathbf{a} · \overrightarrow{AB} = (x, y, z) · (1,0,0) = x$。因为该几何体为正$n$棱柱,所以上底面与下底面对应各顶点的横坐标相等。当$n = 3$时,该几何体为正三棱柱,作出其底面$ABC$的示意图,如图:

则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = \frac{1}{2}$,所以$x = 0$或$\pm \frac{1}{2}$或$\pm 1$,即$A_{3} = \{0, \pm \frac{1}{2}, \pm 1\}$,共有$5$个元素。当$n = 4$时,该几何体为正方体,作出其底面$ABCD$的示意图,如图:

则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = 1$,$x_{D} = 0$,所以$x = 0$或$\pm 1$,即$A_{4} = \{0, \pm 1\}$,共有$3$个元素。当$n = 6$时,该几何体为正六棱柱,作出其底面$ABCDEF$的示意图,如图:

则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = \frac{3}{2}$,$x_{D} = 1$,$x_{E} = 0$,$x_{F} = -\frac{1}{2}$,所以$x = 0$或$\pm \frac{1}{2}$或$\pm 1$或$\pm \frac{3}{2}$或$\pm 2$,即$A_{6} = \{0, \pm \frac{1}{2}, \pm 1, \pm \frac{3}{2}, \pm 2\}$,共有$9$个元素。当$n = 8$时,该几何体为正八棱柱,作出其底面$ABCDEFGH$的示意图,如图:

则$x_{A} = 0$,$x_{B} = 1$,$x_{C} = 1 + \frac{\sqrt{2}}{2}$,$x_{D} = 1 + \frac{\sqrt{2}}{2}$,$x_{E} = 1$,$x_{F} = 0$,$x_{G} = -\frac{\sqrt{2}}{2}$,$x_{H} = -\frac{\sqrt{2}}{2}$,所以$x = 0$或$\pm \frac{\sqrt{2}}{2}$或$\pm 1$或$\pm (1 + \frac{\sqrt{2}}{2})$或$\pm (1 + \sqrt{2})$,即$A_{8} = \{0, \pm \frac{\sqrt{2}}{2}, \pm 1, \pm (1 + \frac{\sqrt{2}}{2}), \pm (1 + \sqrt{2})\}$,共有$9$个元素。综上,当$n = 4$时,$A_{n}$中的元素个数最少。
查看更多完整答案,请扫码查看


