2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第57页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
10. (多选题)已知$\xi$为随机变量,从棱长为1的正方体的12条棱中任取两条,当两条棱相交时,$\xi=0$;当两条棱平行时,$\xi$的值为两条棱之间的距离;当两条棱异面时,$\xi=1$.则下列结论正确的是(
A.共有24对相交棱
B.$P(\xi=0)=\frac{6}{11}$
C.$P(\xi=\sqrt{2})=\frac{1}{11}$
D.$P(\xi=1)=\frac{5}{11}$
AC
)A.共有24对相交棱
B.$P(\xi=0)=\frac{6}{11}$
C.$P(\xi=\sqrt{2})=\frac{1}{11}$
D.$P(\xi=1)=\frac{5}{11}$
答案:
10. AC 若两条棱相交,则交点必为正方体8个顶点中的1个,过任意1个顶点恰有3条棱,所以共有$C_{8}^{2}C_{3}^{2}=24$对相交棱,所以$P(\xi=0)=\frac{24}{C_{12}^{2}}=\frac{4}{11}$,故A正确,B错误;若两条棱平行,则它们的距离为1或$\sqrt{2}$,其中距离为$\sqrt{2}$的共有6对,所以$P(\xi=\sqrt{2})=\frac{6}{C_{12}^{2}}=\frac{1}{11}$,从而$P(\xi=1)=1-P(\xi=0)-P(\xi=\sqrt{2})=1-\frac{4}{11}-\frac{1}{11}=\frac{6}{11}$,故C正确,D错误.
11. 若离散型随机变量$X$的概率分布列为$P(X=n)=\frac{a}{n(n+1)}(n=1,2,3,4)$,其中$a$是常数,则$P(\frac{1}{2}< n<\frac{5}{2})=$
$\frac{5}{6}$
.
答案:
11. $\frac{5}{6}$ 因为$P(X=n)=\frac{a}{n(n+1)}(n=1,2,3,4)$,所以$\frac{a}{2}+\frac{a}{6}+\frac{a}{12}+\frac{a}{20}=1$,解得$a=\frac{5}{4}$,所以$P(\frac{1}{2}<n<\frac{5}{2})=P(X=1)+P(X=2)=\frac{5}{4} × \frac{1}{2}+\frac{5}{4} × \frac{1}{6}=\frac{5}{6}$.
方法总结 求随机变量在某个范围内的概率时,根据概率分布列,将所求范围内各随机变量对应的概率相加即可,其依据是互斥事件的概率加法公式.
方法总结 求随机变量在某个范围内的概率时,根据概率分布列,将所求范围内各随机变量对应的概率相加即可,其依据是互斥事件的概率加法公式.
12. (2023 河北邯郸第一中学月考)如图所示,$A$,$B$两点由5条连线并联,它们在单位时间内能通过的最大信息量依次为2,3,4,3,2.记从中任取3条线且在单位时间内都通过的最大信息总量为$\xi$,则$P(\xi\geq8)=$

$\frac{4}{5}$
.
答案:
12. $\frac{4}{5}$ 解法1(直接法) 由已知得,$\xi$的可能取值为7,8,9,10.因为$P(\xi=7)=\frac{C_{3}^{3}C_{1}^{1}}{C_{5}^{3}}=\frac{1}{5}$,$P(\xi=8)=\frac{C_{3}^{2}C_{2}^{1}}{C_{5}^{3}}=\frac{3}{10}$,$P(\xi=9)=\frac{C_{3}^{1}C_{3}^{2}}{C_{5}^{3}}=\frac{2}{5}$,$P(\xi=10)=\frac{C_{3}^{3}}{C_{5}^{3}}=\frac{1}{10}$,所以$\xi$的概率分布列为
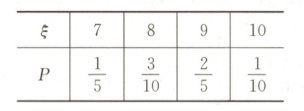
所以$P(\xi\geq8)=P(\xi=8)+P(\xi=9)+P(\xi=10)=\frac{3}{10}+\frac{2}{5}+\frac{1}{10}=\frac{4}{5}$.
解法2(间接法) 由已知得,$\xi$的可能取值为7,8,9,10,故$P(\xi\geq8)$与$P(\xi=7)$是对立事件,所以$P(\xi\geq8)=1-P(\xi=7)=1-\frac{C_{3}^{3}}{C_{5}^{3}}=\frac{4}{5}$.
12. $\frac{4}{5}$ 解法1(直接法) 由已知得,$\xi$的可能取值为7,8,9,10.因为$P(\xi=7)=\frac{C_{3}^{3}C_{1}^{1}}{C_{5}^{3}}=\frac{1}{5}$,$P(\xi=8)=\frac{C_{3}^{2}C_{2}^{1}}{C_{5}^{3}}=\frac{3}{10}$,$P(\xi=9)=\frac{C_{3}^{1}C_{3}^{2}}{C_{5}^{3}}=\frac{2}{5}$,$P(\xi=10)=\frac{C_{3}^{3}}{C_{5}^{3}}=\frac{1}{10}$,所以$\xi$的概率分布列为

所以$P(\xi\geq8)=P(\xi=8)+P(\xi=9)+P(\xi=10)=\frac{3}{10}+\frac{2}{5}+\frac{1}{10}=\frac{4}{5}$.
解法2(间接法) 由已知得,$\xi$的可能取值为7,8,9,10,故$P(\xi\geq8)$与$P(\xi=7)$是对立事件,所以$P(\xi\geq8)=1-P(\xi=7)=1-\frac{C_{3}^{3}}{C_{5}^{3}}=\frac{4}{5}$.
13. (2024 北京期中)某中学校本课程开设了$A$,$B$,$C$,$D$共4门选修课,每个学生必须且只能选修1门选修课,现有该校的甲、乙、丙3名学生,求:
(1) 这3名学生选修课选法的总数;
(2) 恰有2门选修课没有被这3名学生选择的概率;
(3) $A$选修课被这3名学生选择的人数$\xi$的分布列及数学期望.
(1) 这3名学生选修课选法的总数;
(2) 恰有2门选修课没有被这3名学生选择的概率;
(3) $A$选修课被这3名学生选择的人数$\xi$的分布列及数学期望.
答案:
13. 解:
(1) 甲、乙、丙3名同学均可从A,B,C,D共4门选修课中选择1门,故共有$4^{3}=64$种选法.
(2) 恰有2门选修课没有被这3名学生选择,则有2人选择了同一门课程,剩余的1人选择另外一门课程,故有$C_{4}^{2}A_{2}^{2}=36$种选法,则恰有2门选修课没有被这3名学生选择的概率为$\frac{36}{64}=\frac{9}{16}$.
(3) $\xi$的可能取值为0,1,2,3.
$\xi=0$,即3名学生可从B,C,D三门课程中选择一门,共有$3^{3}=27$种情况,则$P(\xi=0)=\frac{3^{3}}{4^{3}}=\frac{27}{64}$;
$\xi=1$,即先从3名学生中选择1名学生选择A课程,剩余的两人可从B,C,D三门课程中选择一门,共有$C_{3}^{1} · 3^{2}$种情况,则$P(\xi=1)=\frac{C_{3}^{1} · 3^{2}}{4^{3}}=\frac{27}{64}$;
$\xi=2$,即先从3名学生中选择2名学生选择A课程,剩余的1人可从B,C,D三门课程中选择一门,共有$C_{3}^{2} · 3$种情况,则$P(\xi=2)=\frac{C_{3}^{2} · 3}{4^{3}}=\frac{9}{64}$;
$\xi=3$,即3名学生均选择A课程,则$P(\xi=3)=\frac{C_{3}^{3}}{4^{3}}=\frac{1}{64}$.
故$\xi$的分布列为
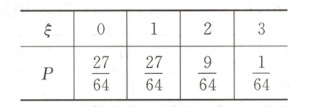
$E(\xi)=0 × \frac{27}{64}+1 × \frac{27}{64}+2 × \frac{9}{64}+3 × \frac{1}{64}=\frac{3}{4}$.
误区警示 求离散型随机变量的分布列后需要检验所有概率之和是否为1.
13. 解:
(1) 甲、乙、丙3名同学均可从A,B,C,D共4门选修课中选择1门,故共有$4^{3}=64$种选法.
(2) 恰有2门选修课没有被这3名学生选择,则有2人选择了同一门课程,剩余的1人选择另外一门课程,故有$C_{4}^{2}A_{2}^{2}=36$种选法,则恰有2门选修课没有被这3名学生选择的概率为$\frac{36}{64}=\frac{9}{16}$.
(3) $\xi$的可能取值为0,1,2,3.
$\xi=0$,即3名学生可从B,C,D三门课程中选择一门,共有$3^{3}=27$种情况,则$P(\xi=0)=\frac{3^{3}}{4^{3}}=\frac{27}{64}$;
$\xi=1$,即先从3名学生中选择1名学生选择A课程,剩余的两人可从B,C,D三门课程中选择一门,共有$C_{3}^{1} · 3^{2}$种情况,则$P(\xi=1)=\frac{C_{3}^{1} · 3^{2}}{4^{3}}=\frac{27}{64}$;
$\xi=2$,即先从3名学生中选择2名学生选择A课程,剩余的1人可从B,C,D三门课程中选择一门,共有$C_{3}^{2} · 3$种情况,则$P(\xi=2)=\frac{C_{3}^{2} · 3}{4^{3}}=\frac{9}{64}$;
$\xi=3$,即3名学生均选择A课程,则$P(\xi=3)=\frac{C_{3}^{3}}{4^{3}}=\frac{1}{64}$.
故$\xi$的分布列为

$E(\xi)=0 × \frac{27}{64}+1 × \frac{27}{64}+2 × \frac{9}{64}+3 × \frac{1}{64}=\frac{3}{4}$.
误区警示 求离散型随机变量的分布列后需要检验所有概率之和是否为1.
14. (2024 辽宁沈阳期中)某地一家新能源汽车工厂对线下的成品车要经过多项检测,检测达标后方可销售,其中关键的两项测试分别为碰撞测试和续航测试,测试的结果只有三种等次:优秀、良好、合格.测试为优秀可得5分,良好可得3分,合格可得1分.该型号新能源汽车在碰撞测试中测试结果为优秀的概率为$\frac{1}{2}$,良好的概率为$\frac{1}{3}$;在续航测试中测试结果为优秀的概率为$\frac{2}{5}$,良好的概率为$\frac{2}{5}$.两项测试相互独立,互不影响,该型号新能源汽车两项测试得分之和记为$\xi$.
(1) 求该型号新能源汽车参加两项测试仅有一项为合格的概率;
(2) 求离散型随机变量$\xi$的分布列与期望.
(1) 求该型号新能源汽车参加两项测试仅有一项为合格的概率;
(2) 求离散型随机变量$\xi$的分布列与期望.
答案:
14. 解:
(1) 记事件$A_{i}$为“该型号新能源汽车参加碰撞测试的得分为$i$分”$(i=1,3,5)$,则$P(A_{5})=\frac{1}{2}$,$P(A_{3})=\frac{1}{3}$,$P(A_{1})=1-\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$.
记事件$B_{i}$为“该型号新能源汽车参加续航测试的得分为$i$分”$(i=1,3,5)$,则$P(B_{5})=\frac{2}{5}$,$P(B_{3})=\frac{2}{5}$,$P(B_{1})=1-\frac{2}{5}-\frac{2}{5}=\frac{1}{5}$.
事件$C$为“该型号新能源汽车参加两项测试仅有一项为合格”,则$P(C)=P(A_{5}B_{1})+P(A_{3}B_{1})+P(A_{1}B_{5})+P(A_{1}B_{3})=\frac{1}{2} × \frac{1}{5}+\frac{1}{3} × \frac{1}{5}+\frac{1}{6} × \frac{2}{5}+\frac{1}{6} × \frac{2}{5}=\frac{3}{10}$,则该型号新能源汽车参加两项测试仅有一项为合格的概率为$\frac{3}{10}$.
(2) 由题知离散型随机变量$\xi$的所有可能取值分别为2,4,6,8,10,$P(\xi=2)=P(A_{3}B_{1})=\frac{1}{6} × \frac{1}{5}=\frac{1}{30}$,$P(\xi=4)=P(A_{3}B_{1})+P(A_{1}B_{3})=\frac{1}{3} × \frac{1}{5}+\frac{1}{6} × \frac{2}{5}=\frac{2}{15}$,$P(\xi=6)=P(A_{5}B_{1})+P(A_{1}B_{5})+P(A_{3}B_{3})=\frac{1}{2} × \frac{1}{5}+\frac{1}{6} × \frac{2}{5}+\frac{1}{3} × \frac{2}{5}=\frac{3}{10}$,$P(\xi=8)=P(A_{3}B_{5})+P(A_{5}B_{3})=\frac{1}{2} × \frac{2}{5}+\frac{1}{3} × \frac{2}{5}=\frac{1}{3}$,$P(\xi=10)=P(A_{5}B_{5})=\frac{1}{2} × \frac{2}{5}=\frac{1}{5}$.
则离散型随机变量$\xi$的分布列为
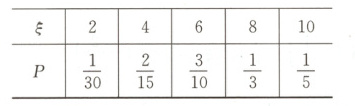
所以数学期望$E(\xi)=2 × \frac{1}{30}+4 × \frac{2}{15}+6 × \frac{3}{10}+8 × \frac{1}{3}+10 × \frac{1}{5}=\frac{106}{15}$.
14. 解:
(1) 记事件$A_{i}$为“该型号新能源汽车参加碰撞测试的得分为$i$分”$(i=1,3,5)$,则$P(A_{5})=\frac{1}{2}$,$P(A_{3})=\frac{1}{3}$,$P(A_{1})=1-\frac{1}{2}-\frac{1}{3}=\frac{1}{6}$.
记事件$B_{i}$为“该型号新能源汽车参加续航测试的得分为$i$分”$(i=1,3,5)$,则$P(B_{5})=\frac{2}{5}$,$P(B_{3})=\frac{2}{5}$,$P(B_{1})=1-\frac{2}{5}-\frac{2}{5}=\frac{1}{5}$.
事件$C$为“该型号新能源汽车参加两项测试仅有一项为合格”,则$P(C)=P(A_{5}B_{1})+P(A_{3}B_{1})+P(A_{1}B_{5})+P(A_{1}B_{3})=\frac{1}{2} × \frac{1}{5}+\frac{1}{3} × \frac{1}{5}+\frac{1}{6} × \frac{2}{5}+\frac{1}{6} × \frac{2}{5}=\frac{3}{10}$,则该型号新能源汽车参加两项测试仅有一项为合格的概率为$\frac{3}{10}$.
(2) 由题知离散型随机变量$\xi$的所有可能取值分别为2,4,6,8,10,$P(\xi=2)=P(A_{3}B_{1})=\frac{1}{6} × \frac{1}{5}=\frac{1}{30}$,$P(\xi=4)=P(A_{3}B_{1})+P(A_{1}B_{3})=\frac{1}{3} × \frac{1}{5}+\frac{1}{6} × \frac{2}{5}=\frac{2}{15}$,$P(\xi=6)=P(A_{5}B_{1})+P(A_{1}B_{5})+P(A_{3}B_{3})=\frac{1}{2} × \frac{1}{5}+\frac{1}{6} × \frac{2}{5}+\frac{1}{3} × \frac{2}{5}=\frac{3}{10}$,$P(\xi=8)=P(A_{3}B_{5})+P(A_{5}B_{3})=\frac{1}{2} × \frac{2}{5}+\frac{1}{3} × \frac{2}{5}=\frac{1}{3}$,$P(\xi=10)=P(A_{5}B_{5})=\frac{1}{2} × \frac{2}{5}=\frac{1}{5}$.
则离散型随机变量$\xi$的分布列为

所以数学期望$E(\xi)=2 × \frac{1}{30}+4 × \frac{2}{15}+6 × \frac{3}{10}+8 × \frac{1}{3}+10 × \frac{1}{5}=\frac{106}{15}$.
15. 已知一个口袋中有3个白球、3个黑球,这些球除颜色外全部相同.现将口袋中的球随机地逐个取出,并放入如图所示的编号为1,2,3,$·s$,6的抽屉内,其中第$k$次取出的球放入编号为$k$的抽屉($k=1,2,3,·s,6$).

(1) 试求编号为2的抽屉内放的是黑球的概率$P$;
(2) 随机变量$X$表示最后一个取出的黑球所在抽屉的编号,求$X$的分布列.

(1) 试求编号为2的抽屉内放的是黑球的概率$P$;
(2) 随机变量$X$表示最后一个取出的黑球所在抽屉的编号,求$X$的分布列.
答案:
15.
(1) 解法1 编号为2的抽屉内放的是黑球的概率$P=\frac{C_{3}^{1}C_{3}^{1}+C_{3}^{1}C_{2}^{1}}{C_{6}^{1}C_{5}^{1}}=\frac{15}{30}=\frac{1}{2}$.
解法2 编号为2的抽屉内放的是黑球的概率$P=\frac{1}{2} × \frac{3}{5}+\frac{1}{2} × \frac{2}{5}=\frac{1}{2}$.
(2) 解法1 随机变量$X$的取值有3,4,5,6.$P(X=3)=\frac{A_{3}^{3}}{A_{6}^{3}}=\frac{6}{120}=\frac{1}{20}$,$P(X=4)=\frac{C_{3}^{1}C_{3}^{1}A_{2}^{2}}{A_{6}^{4}}=\frac{9 × 6}{360}=\frac{3}{20}$,$P(X=5)=\frac{C_{3}^{2}A_{2}^{2}A_{3}^{3}}{A_{6}^{5}}=\frac{6 × 6 × 6}{720}=\frac{3}{10}$,$P(X=6)=\frac{C_{3}^{3}A_{3}^{3}A_{3}^{3}}{A_{6}^{6}}=\frac{10 × 6 × 6}{720}=\frac{1}{2}$.
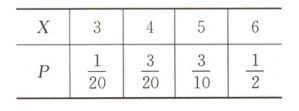
所以随机变量$X$的分布列为
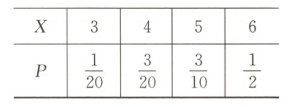
解法2 随机变量$X$的取值有3,4,5,6.$P(X=3)=\frac{1}{C_{6}^{3}}=\frac{1}{20}$,$P(X=4)=\frac{C_{3}^{2}}{C_{6}^{3}}=\frac{3}{20}$,$P(X=5)=\frac{C_{3}^{2}}{C_{6}^{3}}=\frac{3}{10}$,$P(X=6)=\frac{C_{3}^{3}}{C_{6}^{3}}=\frac{1}{2}$.
所以随机变量$X$的分布列为
15.
(1) 解法1 编号为2的抽屉内放的是黑球的概率$P=\frac{C_{3}^{1}C_{3}^{1}+C_{3}^{1}C_{2}^{1}}{C_{6}^{1}C_{5}^{1}}=\frac{15}{30}=\frac{1}{2}$.
解法2 编号为2的抽屉内放的是黑球的概率$P=\frac{1}{2} × \frac{3}{5}+\frac{1}{2} × \frac{2}{5}=\frac{1}{2}$.
(2) 解法1 随机变量$X$的取值有3,4,5,6.$P(X=3)=\frac{A_{3}^{3}}{A_{6}^{3}}=\frac{6}{120}=\frac{1}{20}$,$P(X=4)=\frac{C_{3}^{1}C_{3}^{1}A_{2}^{2}}{A_{6}^{4}}=\frac{9 × 6}{360}=\frac{3}{20}$,$P(X=5)=\frac{C_{3}^{2}A_{2}^{2}A_{3}^{3}}{A_{6}^{5}}=\frac{6 × 6 × 6}{720}=\frac{3}{10}$,$P(X=6)=\frac{C_{3}^{3}A_{3}^{3}A_{3}^{3}}{A_{6}^{6}}=\frac{10 × 6 × 6}{720}=\frac{1}{2}$.
所以随机变量$X$的分布列为

解法2 随机变量$X$的取值有3,4,5,6.$P(X=3)=\frac{1}{C_{6}^{3}}=\frac{1}{20}$,$P(X=4)=\frac{C_{3}^{2}}{C_{6}^{3}}=\frac{3}{20}$,$P(X=5)=\frac{C_{3}^{2}}{C_{6}^{3}}=\frac{3}{10}$,$P(X=6)=\frac{C_{3}^{3}}{C_{6}^{3}}=\frac{1}{2}$.
所以随机变量$X$的分布列为

查看更多完整答案,请扫码查看


