2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第11页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
15. (2024湖北阶段练习)空间中,两两互相垂直且有公共原点的三条数轴构成空间直角坐标系。如果坐标系中有两条坐标轴互相不垂直,那么这样的坐标系称为“斜坐标系”。现有一种空间斜坐标系,它的任意两条数轴的夹角均为$ 60° $,我们将这种坐标系称为“斜$ 60° $坐标系”。我们类比空间直角坐标系,定义“空间斜$ 60° $坐标系”下向量的斜$ 60° $坐标:$ \boldsymbol{i},\boldsymbol{j},\boldsymbol{k} $分别为“斜$ 60° $坐标系”下三条数轴($ x $轴、$ y $轴、$ z $轴)正方向上的单位向量,若向量$ \boldsymbol{n}=x\boldsymbol{i}+y\boldsymbol{j}+z\boldsymbol{k} $,则$ \boldsymbol{n} $与有序实数组$ [x,y,z] $一一对应,称向量$ \boldsymbol{n} $的斜$ 60° $坐标为$ [x,y,z] $,记作$ \boldsymbol{n}=[x,y,z] $。
(1) 若$ \boldsymbol{a}=[1,2,3] $,$ \boldsymbol{b}=[-1,1,2] $,求$ \boldsymbol{a}+\boldsymbol{b} $的斜$ 60° $坐标。
(2) 在平行六面体$ ABCD - A_1B_1C_1D_1 $中,$ AB = AD = 2 $,$ AA_1 = 3 $,$ \angle BAD = \angle BAA_1 = \angle DAA_1 = 60° $,建立“空间斜$ 60° $坐标系”如图所示。
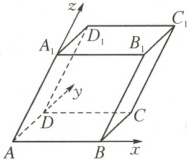
①若$ \overrightarrow{BE}=\overrightarrow{EB_1} $,求向量$ \overrightarrow{ED_1} $的斜$ 60° $坐标;
②若$ \overrightarrow{AM}=[3,t,0] $,且$ \overrightarrow{AM}\perp\overrightarrow{AC_1} $,求$ |\overrightarrow{AM}| $。
(1) 若$ \boldsymbol{a}=[1,2,3] $,$ \boldsymbol{b}=[-1,1,2] $,求$ \boldsymbol{a}+\boldsymbol{b} $的斜$ 60° $坐标。
(2) 在平行六面体$ ABCD - A_1B_1C_1D_1 $中,$ AB = AD = 2 $,$ AA_1 = 3 $,$ \angle BAD = \angle BAA_1 = \angle DAA_1 = 60° $,建立“空间斜$ 60° $坐标系”如图所示。

①若$ \overrightarrow{BE}=\overrightarrow{EB_1} $,求向量$ \overrightarrow{ED_1} $的斜$ 60° $坐标;
②若$ \overrightarrow{AM}=[3,t,0] $,且$ \overrightarrow{AM}\perp\overrightarrow{AC_1} $,求$ |\overrightarrow{AM}| $。
答案:
15.解:
(1)因为a=[1,2,3],b=[-1,1,2],
所以a + b=(i + 2j + 3k)+(-i + j + 2k)=3j + 5k=[0,3,5],所以a + b的斜60°坐标为[0,3,5].
(2)设i,j,k分别为与$\overrightarrow{AB}$,$\overrightarrow{AD}$,$\overrightarrow{AA₁}$同方向的单位向量,
则$\overrightarrow{AB}$ = 2i,$\overrightarrow{AD}$ = 2j,$\overrightarrow{AA₁}$ = 3k.
①$\overrightarrow{ED₁}=\overrightarrow{AD₁}-\overrightarrow{AE}=(\overrightarrow{AD}+\overrightarrow{AA₁})-(\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AA₁})=- \overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA₁}=-2i + 2j+\frac{3}{2}k=[-2,2,\frac{3}{2}]$
②由题得$\overrightarrow{AC₁}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA₁}=2i + 2j + 3k$.
由$\overrightarrow{AM}$ = [3,t,0],知$\overrightarrow{AM}$ = 3i + tj.
易知i·j = i·k = j·k = 1×1×$\frac{1}{2}=\frac{1}{2}$.
由$\overrightarrow{AM}⊥\overrightarrow{AC₁}$,知$\overrightarrow{AM}·\overrightarrow{AC₁}$=(3i + tj)·(2i + 2j + 3k)=0,
所以6i² + 2tj²+(6 + 2t)i·j + 9k·i + 3tk·j = 0,
所以6 + 2t+$\frac{6 + 2t}{2}+\frac{9}{2}+\frac{3t}{2}$ = 0,解得t = -3,
则$|\overrightarrow{AM}|=|3i - 3j|=\sqrt{(3i - 3j)²}=3$.
(1)因为a=[1,2,3],b=[-1,1,2],
所以a + b=(i + 2j + 3k)+(-i + j + 2k)=3j + 5k=[0,3,5],所以a + b的斜60°坐标为[0,3,5].
(2)设i,j,k分别为与$\overrightarrow{AB}$,$\overrightarrow{AD}$,$\overrightarrow{AA₁}$同方向的单位向量,
则$\overrightarrow{AB}$ = 2i,$\overrightarrow{AD}$ = 2j,$\overrightarrow{AA₁}$ = 3k.
①$\overrightarrow{ED₁}=\overrightarrow{AD₁}-\overrightarrow{AE}=(\overrightarrow{AD}+\overrightarrow{AA₁})-(\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AA₁})=- \overrightarrow{AB}+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AA₁}=-2i + 2j+\frac{3}{2}k=[-2,2,\frac{3}{2}]$
②由题得$\overrightarrow{AC₁}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA₁}=2i + 2j + 3k$.
由$\overrightarrow{AM}$ = [3,t,0],知$\overrightarrow{AM}$ = 3i + tj.
易知i·j = i·k = j·k = 1×1×$\frac{1}{2}=\frac{1}{2}$.
由$\overrightarrow{AM}⊥\overrightarrow{AC₁}$,知$\overrightarrow{AM}·\overrightarrow{AC₁}$=(3i + tj)·(2i + 2j + 3k)=0,
所以6i² + 2tj²+(6 + 2t)i·j + 9k·i + 3tk·j = 0,
所以6 + 2t+$\frac{6 + 2t}{2}+\frac{9}{2}+\frac{3t}{2}$ = 0,解得t = -3,
则$|\overrightarrow{AM}|=|3i - 3j|=\sqrt{(3i - 3j)²}=3$.
查看更多完整答案,请扫码查看


