2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第41页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. (2024 内蒙古期中)从6人(包含甲)中选派出3人参加A,B,C这三项不同的活动,且每项活动有且仅有1人参加.若甲不参加A和B活动,则不同的选派方案有 (
A.60种
B.80种
C.90种
D.150种
B
)A.60种
B.80种
C.90种
D.150种
答案:
1.B 当甲被选中时,不同的选派方案有$A_{5}^{2}=20$种;当甲未被选中时,不同的选派方案有$A_{5}^{3}=60$种.故满足条件的不同的选派方案有$20 + 60 = 80$种.
方法总结 某个或几个元素要排在指定位置或不排在指定位置,则优先考虑这些元素或这些位置,将它们排在某个位置或不排在某个位置上.有时,我们也可以先不考虑这些特殊的元素或位置而进行全排,然后将不满足条件的排列数去除,即采用间接法来进行求解.
方法总结 某个或几个元素要排在指定位置或不排在指定位置,则优先考虑这些元素或这些位置,将它们排在某个位置或不排在某个位置上.有时,我们也可以先不考虑这些特殊的元素或位置而进行全排,然后将不满足条件的排列数去除,即采用间接法来进行求解.
2. (2024 广东期中)某种产品的加工需要经过A,B,C,D,E,F,G七道工序,要求A,B两道工序必须相邻,C,D两道工序不能相邻,则不同的加工顺序有 (
A.960种
B.836种
C.816种
D.720种
A
)A.960种
B.836种
C.816种
D.720种
答案:
2.A 先捆绑A,B,再和E,F,G排列,最后插入C,D,共有$A_{2}^{2}A_{4}^{1}A_{2}^{2}=2× 24× 20=960$种加工顺序.
方法总结 某些元素要求相邻,则将这些元素捆绑在一起,将它作为一个元素与剩余的元素进行排列,此为捆绑法;若某些元素要求不相邻,则采用插空法,即先将其他的元素进行排列,然后将要求不相邻的元素插入这些元素排列后产生的空位中.
方法总结 某些元素要求相邻,则将这些元素捆绑在一起,将它作为一个元素与剩余的元素进行排列,此为捆绑法;若某些元素要求不相邻,则采用插空法,即先将其他的元素进行排列,然后将要求不相邻的元素插入这些元素排列后产生的空位中.
3. 现今,网上购物已经成为人们购物的一种主流.因保管不善,四个快递A,B,C,D上送货地址模糊不清,但快递小哥记得这四个快递应分别送去甲、乙、丙、丁四个地方,全部送错的概率是 (
A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{3}{8}$
D.$\frac{5}{12}$
C
)A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{3}{8}$
D.$\frac{5}{12}$
答案:
3.C 解法1 不妨设甲、乙、丙、丁四个地址对应的快递为A,B,C,D.由题意,某地址(不妨设甲地)快递送错的情况有3种,据此将快递送错分为三类,我们用“树状图”表示如下:

所以共有9种不同的送错方式,而总共有$A_{4}^{4}=24$种可能,所以全部选错的概率$P=\frac{9}{24}=\frac{3}{8}$.
解法2 若全部送错,则每个快递都送到了其他的地方,即送A 有3种送错可能,若A送到某地应该送的地方,则此地有3种送错可能,故全部送错的情况有$3× 3=9$种可能,而总共有$A_{4}^{4}=24$种可能,所以全部选错的概率$P=\frac{9}{24}=\frac{3}{8}$.
方法总结 1.对于一些实际操作问题,若没有一般的求解方法,我们就可以采用最为直接的方法——枚举法来加以求解.
2.本题的模型称为错排问题,对于此类问题,我们还可以采用配对方式,即解法2所采用的方法.
3.C 解法1 不妨设甲、乙、丙、丁四个地址对应的快递为A,B,C,D.由题意,某地址(不妨设甲地)快递送错的情况有3种,据此将快递送错分为三类,我们用“树状图”表示如下:

所以共有9种不同的送错方式,而总共有$A_{4}^{4}=24$种可能,所以全部选错的概率$P=\frac{9}{24}=\frac{3}{8}$.
解法2 若全部送错,则每个快递都送到了其他的地方,即送A 有3种送错可能,若A送到某地应该送的地方,则此地有3种送错可能,故全部送错的情况有$3× 3=9$种可能,而总共有$A_{4}^{4}=24$种可能,所以全部选错的概率$P=\frac{9}{24}=\frac{3}{8}$.
方法总结 1.对于一些实际操作问题,若没有一般的求解方法,我们就可以采用最为直接的方法——枚举法来加以求解.
2.本题的模型称为错排问题,对于此类问题,我们还可以采用配对方式,即解法2所采用的方法.
4. (2024 山东枣庄期末)将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分配到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有 (
A.60种
B.120种
C.240种
D.480种
C
)A.60种
B.120种
C.240种
D.480种
答案:
4.C 由题意知,有一个项目分配2名志愿者,其余各项目分配1名志愿者.先从5名志愿者中任选2人,组成一个小组,有$C_{5}^{2}$种选法,然后连同其余三人,看成四个元素,四个项目看成四个不同的位置,四个不同的元素在四个不同的位置的排列方法数有4!种.根据乘法原理,共有$C_{5}^{2}× 4!=240$种不同的分配方案.
方法总结 在研究排列组合的综合问题时,一般采用先选后排的策略.
方法总结 在研究排列组合的综合问题时,一般采用先选后排的策略.
5. (2023 河北石家庄期中)某五面体木块的直观图如图所示.现准备给其5个面涂色,每个面涂一种颜色,且相邻两个面(有公共棱的两个面)所涂颜色不能相同.若有6种不同颜色的颜料可供选择,则不同的涂色方案有 (
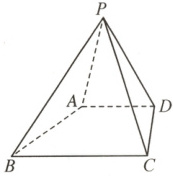
A.600种
B.1080种
C.1200种
D.1560种
D
)
A.600种
B.1080种
C.1200种
D.1560种
答案:
5.D 若用5种颜色,从6种颜色中任选5种再做全排,即$A_{6}^{5}=720$种;若用4种颜色,从6种颜色中任选4种有$C_{6}^{4}=15$种,再任选一种颜色涂在其中一组对面上,有$C_{4}^{1}C_{2}^{1}=8$种,其他3种颜色做全排列有$A_{3}^{3}=6$种,所以共有$15× 8× 6=720$种;若用3种颜色,从6种颜色中任选3种有$C_{6}^{3}=20$种,再任选两种颜色涂在两组对面上,有$A_{3}^{2}=6$种,余下的一种颜色涂在底面,有1种,所以共有$20× 6× 1=120$种.综上,不同的涂色方案有$720 + 720 + 120 = 1560$种.
方法总结 涂色问题的常用方法:
(1)根据共用了多少种颜色分类讨论;
(2)根据相对区域是否同色分类讨论.
方法总结 涂色问题的常用方法:
(1)根据共用了多少种颜色分类讨论;
(2)根据相对区域是否同色分类讨论.
6. (多选题,2024 江苏镇江期中)定义“圆排列”:从n个不同元素中选m个元素围成一个圆形,称为圆排列,所有圆排列的方法数计为$H_{n}^{m}$.圆排列是排列的一种,区别于通常的“直线排列”,既无“头”也无“尾”,所以$H_{n}^{m}=\frac{A_{n}^{m}}{m}$.现有2个女生、4个男生,共6名同学围坐成一圈,做击鼓传花的游戏,则 (
A.共有$H_{6}^{6}$种排法
B.若两名女生相邻,则有$2H_{5}^{5}$种排法
C.若两名女生不相邻,共有$4H_{4}^{4}$种排法
D.若男生甲位置固定,则有$5H_{5}^{5}$种排法
ABD
)A.共有$H_{6}^{6}$种排法
B.若两名女生相邻,则有$2H_{5}^{5}$种排法
C.若两名女生不相邻,共有$4H_{4}^{4}$种排法
D.若男生甲位置固定,则有$5H_{5}^{5}$种排法
答案:
6.ABD 对于A,2个女生、4个男生共6名同学围坐成一圈,共有$\frac{A_{6}^{6}}{6}=H_{6}^{}$种排法,故A正确;对于B,若两名女生相邻,则有$A_{2}^{2}A_{5}^{5}{5}÷ 5=2H_{5}^{}$种排法,故B正确;对于C,若两名女生不相邻,则有$\frac{A_{4}^{4}A_{5}^{2}}{4× 5}=12H_{3}^{}$种排法,故C错误;对于D,若男生甲位置固定,考虑以甲为基准的顺、逆时针排列,则有$A_{5}^{3}=5H_{5}^{}$种排法,故D正确.
方法总结 对于环排问题(也叫作圆排列问题)通常采用先固定一个元素,然后将它转化为直线排列问题.
方法总结 对于环排问题(也叫作圆排列问题)通常采用先固定一个元素,然后将它转化为直线排列问题.
7. (多选题,2024 吉林期中)下列说法正确的是 (
A.6本不同的书分给甲、乙、丙三人,每人两本,有$C_{6}^{2}C_{4}^{2}C_{2}^{2}$种不同的分法
B.6本相同的书分给甲、乙、丙三人,每人两本,有540种不同的分法
C.6本相同的书分给甲、乙、丙三人,每人至少一本,有10种不同的分法
D.6本不同的书分给甲、乙、丙三人,其中一人1本,一人2本,一人3本,有$C_{6}^{1}C_{5}^{2}C_{3}^{3}$种不同的分法
AC
)A.6本不同的书分给甲、乙、丙三人,每人两本,有$C_{6}^{2}C_{4}^{2}C_{2}^{2}$种不同的分法
B.6本相同的书分给甲、乙、丙三人,每人两本,有540种不同的分法
C.6本相同的书分给甲、乙、丙三人,每人至少一本,有10种不同的分法
D.6本不同的书分给甲、乙、丙三人,其中一人1本,一人2本,一人3本,有$C_{6}^{1}C_{5}^{2}C_{3}^{3}$种不同的分法
答案:
7.AC 对于A,6本不同的书中,先取2本给甲,再从剩余的4本中取2本给乙,最后2本给丙,共有$C_{6}^{2}C_{4}^{2}C_{2}^{2}$种不同的分法,故A正确;对于B,6本相同的书分给甲、乙、丙三人,每人两本,有1种分法,故B错误;对于C,6本相同的书分给甲、乙、丙三人,利用隔板法,共有$C_{6}^{2}=10$种,故C正确;对于D,6本不同的书中,先取1本作为一组,再从剩余的5本中取2本作为一组,最后3本作为一组,共有$C_{6}^{1}C_{5}^{2}C_{3}^{3}=60$种,再将3组分给甲、乙、丙三人,共有$C_{6}^{1}C_{5}^{2}C_{3}^{3}A_{3}^{3}=360$种,故D错误.
方法总结 1.对于不同元素的分组问题,有平均分组、不平均分组以及部分平均分组.对于平均分组问题或部分平均分组中的平均分组问题,需要应用除法策略来去除平均分组中的“序”.若平均分组数为$n$,则需除以$A_{n}^{n}$.
2.对于分组分配问题,一般采用分步计数原理来加以解决,即先分组,然后再分配.
方法总结 1.对于不同元素的分组问题,有平均分组、不平均分组以及部分平均分组.对于平均分组问题或部分平均分组中的平均分组问题,需要应用除法策略来去除平均分组中的“序”.若平均分组数为$n$,则需除以$A_{n}^{n}$.
2.对于分组分配问题,一般采用分步计数原理来加以解决,即先分组,然后再分配.
8. (多选题,2025 全国模拟预测)将1,2,3,4,5,6,7这七个数随机地排成一个数列,记第i项为$a_{i}(i=1,2,·s,7)$,则下列说法正确的是(
A.若$a_{4}=7$,$a_{1}+a_{2}+a_{3}\lt a_{5}+a_{6}+a_{7}$,则这样的数列共有360个
B.若该数列恰好先减后增,则这样的数列共有64个
C.若所有的奇数不相邻,所有的偶数也不相邻,则这样的数列共有144个
D.若$a_{1}\gt a_{2}\gt a_{3}$,$a_{3}\lt a_{4}\lt a_{5}$,$a_{5}\gt a_{6}\gt a_{7}$,则这样的数列共有71个
ACD
)A.若$a_{4}=7$,$a_{1}+a_{2}+a_{3}\lt a_{5}+a_{6}+a_{7}$,则这样的数列共有360个
B.若该数列恰好先减后增,则这样的数列共有64个
C.若所有的奇数不相邻,所有的偶数也不相邻,则这样的数列共有144个
D.若$a_{1}\gt a_{2}\gt a_{3}$,$a_{3}\lt a_{4}\lt a_{5}$,$a_{5}\gt a_{6}\gt a_{7}$,则这样的数列共有71个
答案:
8.ACD 对于A,由于$1 + 2 + 3 + 4 + 5 + 6 = 21$为奇数,根据对称性可知这样的数列有$\frac{C_{6}^{3}}{2}· A_{3}^{3}· A_{3}^{3}=360$个,故A正确;对于B,从2,3,4,5,6,7中选出1个数排在1的右侧,其余排在1的左侧,得到先减后增的数列有$C_{6}^{3}$个,从2,3,4,5,6,7中选出3个数排在1的右侧,其余排在1的左侧,得到先减后增的数列有$C_{6}^{3}$个,从2,3,4,5,6,7中选出4个数排在1的右侧,其余排在1的左侧,得到先减后增的数列有$C_{6}^{3}$个,从2,3,4,5,6,7中选出5个数排在1的右侧,其余排在1的左侧,得到先减后增的数列有$C_{6}^{3}$个,故满足条件的总个数为$C_{6}^{3}+C_{6}^{3}+C_{6}^{3}+C_{6}^{3}+C_{6}^{3}=62$,故B错误;对于C,若所有的奇数不相邻,所有的偶数也不相邻,则这样的数列只能是“奇、偶、奇、偶、奇、偶、奇”,则有$A_{4}^{4}A_{3}^{3}=144$个,故C正确;对于D,若$a_{3}=1$,则先从其余6个数中任选2个数作为$a_{1}$,$a_{2}$,且$a_{1}>a_{2}$,有$C_{6}^{2}$种方法,剩余4个数中最大的为$a_{5}$,剩下的3个数任取2个作为$a_{6}$,$a_{7}$,且$a_{6}>a_{7}$,有$C_{3}^{2}$种方法,则这样的数列有$C_{6}^{2}C_{3}^{2}=45$种;若$a_{3}=2$,则先从除去1之外的5个数中任选2个数作为$a_{1}$,$a_{2}$,且$a_{1}>a_{2}$,有$C_{5}^{2}$种方法,剩余4个数中最大的为$a_{5}$,$a_{7}=1$,剩下的2个数任取1个作为$a_{6}$或$a_{4}$即可,有$C_{2}^{1}$种方法,则这样的数列有$C_{5}^{2}C_{2}^{1}=10× 2=20$种,若$a_{3}=3$,则先从除去1,2之外的4个数中任选2个数作为$a_{1}$,$a_{2}$,且$a_{1}>a_{2}$,有$C_{4}^{2}$种方法,剩余4个数位置固定,只有一种排法,其中$a_{6}=2$,$a_{7}=1$,则这样的数列有$C_{4}^{2}=6$种,若$a_{3}=4,5,6,7$,均不存在这样的数列.所以满足条件的数列共有$45 + 20 + 6 = 71$个.
9. (多选题,2024 山西期中)某高中打算组建一个校园足球队,计划从各班挑选11个同学.下列说法正确的是 (
A.若将校足球队的11个名额分到8个班级,每个班级至少1个名额,共有240种分配方法
B.学校教练计划比赛前将对除指定的守门员外的其他10名队员进行分组训练.若其中一组4人,另外两组每组3人,有2100种不同的分组方式
C.比赛入场时,工作人员会为11名队员拍集体照,若要求拍照时A,B,C三人必须相邻,D,E,F,G四人均不相邻,有259200种不同的排法
D.现安排A,B,C三名同学到甲、乙、丙、丁四个球队进行集训,若甲球队必须有同学去,则不同的安排方法有37种
BCD
)A.若将校足球队的11个名额分到8个班级,每个班级至少1个名额,共有240种分配方法
B.学校教练计划比赛前将对除指定的守门员外的其他10名队员进行分组训练.若其中一组4人,另外两组每组3人,有2100种不同的分组方式
C.比赛入场时,工作人员会为11名队员拍集体照,若要求拍照时A,B,C三人必须相邻,D,E,F,G四人均不相邻,有259200种不同的排法
D.现安排A,B,C三名同学到甲、乙、丙、丁四个球队进行集训,若甲球队必须有同学去,则不同的安排方法有37种
答案:
9.BCD 对于选项A,问题等价于将11个完全相同的小球分为8组,每组至少一个小球,由隔板法可知,不同的分配方法种数为$C_{10}^{7}=120$,故A错误;对于选项B,将对除指定的守门员外的其他10名队员进行分组训练,若其中一组4人,另外两组每组3人,则不同的方法种数为$\frac{C_{10}^{4}C_{6}^{3}C_{3}^{3}}{A_{2}^{2}}=\frac{210× 20}{2}=2100$,故B正确;对于选项C,将A,B,C三人进行捆绑,与除D,E,F,G 四人以外的4人进行全排,再将D,E,F,G四人进行插空,所以不同的排法种数为$A_{3}^{3}A_{6}^{6}A_{4}^{4}=6× 120× 360=259200$,故C正确;对于选项D,采用间接法,所有选法是$4× 4× 4=64$种,甲球队没有同学去有$3× 3× 3=27$种,故甲球队必须有同学去有$64−27=37$种,故D正确.
方法总结 求解相同元素分组问题通常采用隔板的方法,即将相同的元素用若干个隔板隔成若干份,每一种不同的隔法就对应着一种不同的分法,所有分隔方法数即为所求的方法数.
方法总结 求解相同元素分组问题通常采用隔板的方法,即将相同的元素用若干个隔板隔成若干份,每一种不同的隔法就对应着一种不同的分法,所有分隔方法数即为所求的方法数.
查看更多完整答案,请扫码查看


