2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第27页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
1. (2023 全国甲卷理,11)已知四棱锥 $ P - ABCD $ 的底面是边长为 4 的正方形, $ PC = PD = 3 $, $ \angle PCA = 45° $,则 $ \triangle PBC $ 的面积为 (
A.$ 2\sqrt{2} $
B.$ 3\sqrt{2} $
C.$ 4\sqrt{2} $
D.$ 6\sqrt{2} $
C
)A.$ 2\sqrt{2} $
B.$ 3\sqrt{2} $
C.$ 4\sqrt{2} $
D.$ 6\sqrt{2} $
答案:
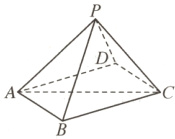
1.C 解法1 分析:由$PC=PD$不难想到点$P$在边$CD$的垂直平分面上.又因为底面$ABCD$为正方形,可得$PA=PB$,再在$\triangle PAC$中利用余弦定理求得$PA=PB=\sqrt{17}$,由此在$\triangle PBC$中利用余弦定理与三角形面积公式即可得解.
如图,连接$AC$.由$PC=PD$知,点$P$在边$CD$的垂直平分面上,又因为底面$ABCD$为正方形,所以点$P$也在边$AB$的垂直平分面上,所以$PA=PB$.在$\triangle PAC$中,$PC=3$,$AC=4\sqrt{2}$,$\angle PCA=45^{\circ}$,则由余弦定理可得$PA^{2}=AC^{2}+PC^{2}-2AC· PC\cos\angle PCA=32+9 - 2×4\sqrt{2}×3×\frac{\sqrt{2}}{2}=17$,故$PB=PA=\sqrt{17}$.在$\triangle PBC$中,$PC=3$,$PB=\sqrt{17}$,$BC=4$,所以$\cos\angle PCB=\frac{PC^{2}+BC^{2}-PB^{2}}{2PC· BC}=\frac{9 + 16-17}{2×3×4}=\frac{1}{3}$.又$0<\angle PCB<\pi$,所以$\sin\angle PCB=\sqrt{1-\cos^{2}\angle PCB}=\frac{2\sqrt{2}}{3}$.所以$\triangle PBC$的面积为$S=\frac{1}{2}PC· BC·\sin\angle PCB=\frac{1}{2}×3×4×\frac{2\sqrt{2}}{3}=4\sqrt{2}$.
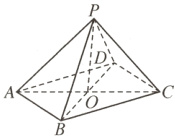
解法2 分析:欲求$\triangle PBC$的面积,而已知$PC=3$,$BC=4$,则只需需求出$\triangle PBC$的边$PB$即可.又因为$\triangle POC(O$为对角线$AC$和$BD$的交点)可解,所以可借助关系式$\overrightarrow{PB}·\overrightarrow{PD}=\overrightarrow{PO}^{2}-\overrightarrow{OB}^{2}=\frac{PD^{2}+PB^{2}-BD^{2}}{2}$求出边$PB$的长.
如图,连接$AC$,$BD$交于点$O$,连接$PO$,则$O$为$AC$,$BD$的中点.在$\triangle POC$中,$PO^{2}=OC^{2}+PC^{2}-2OC· PC\cos\angle PCA=8 + 9-2×2\sqrt{2}×3×\frac{\sqrt{2}}{2}=5$,由$\overrightarrow{PB}·\overrightarrow{PD}=\overrightarrow{PO}^{2}-\overrightarrow{OB}^{2}=\frac{PD^{2}+PB^{2}-BD^{2}}{2}$,得$5-8=\frac{3^{2}+PB^{2}-32}{2}$,即$PB=\sqrt{17}$.在$\triangle PBC$中,$PC=3$,$PB=\sqrt{17}$,$BC=4$,所以$\cos\angle PCB=\frac{PC^{2}+BC^{2}-PB^{2}}{2PC· BC}=\frac{9 + 16-17}{2×3×4}=\frac{1}{3}$.又$0<\angle PCB<\pi$,所以$\sin\angle PCB=\sqrt{1-\cos^{2}\angle PCB}=\frac{2\sqrt{2}}{3}$.所以$\triangle PBC$的面积为$S=\frac{1}{2}PC· BC\sin\angle PCB=\frac{1}{2}×3×4×\frac{2\sqrt{2}}{3}=4\sqrt{2}$.
解后反思 解法1和解法2都是求边$PB$的长,但是选择的方法不同,解法1借助于基本事实:到线段两端点距离相等的点在线段的垂直平分面上,从而可得$PB=PA$,进而解三角形.解法2是根据$PO$是$\triangle PBD$的中线,借助向量数量积$\overrightarrow{PB}·\overrightarrow{PD}$的两种表示形式建立等式关系求解,当然也可以直接用二级结论:$(2PO)^{2}+DB^{2}=2(PB^{2}+PD^{2})$来求解边$PB$的长度.两种解法各有千秋,都需要掌握.
1.C 解法1 分析:由$PC=PD$不难想到点$P$在边$CD$的垂直平分面上.又因为底面$ABCD$为正方形,可得$PA=PB$,再在$\triangle PAC$中利用余弦定理求得$PA=PB=\sqrt{17}$,由此在$\triangle PBC$中利用余弦定理与三角形面积公式即可得解.
如图,连接$AC$.由$PC=PD$知,点$P$在边$CD$的垂直平分面上,又因为底面$ABCD$为正方形,所以点$P$也在边$AB$的垂直平分面上,所以$PA=PB$.在$\triangle PAC$中,$PC=3$,$AC=4\sqrt{2}$,$\angle PCA=45^{\circ}$,则由余弦定理可得$PA^{2}=AC^{2}+PC^{2}-2AC· PC\cos\angle PCA=32+9 - 2×4\sqrt{2}×3×\frac{\sqrt{2}}{2}=17$,故$PB=PA=\sqrt{17}$.在$\triangle PBC$中,$PC=3$,$PB=\sqrt{17}$,$BC=4$,所以$\cos\angle PCB=\frac{PC^{2}+BC^{2}-PB^{2}}{2PC· BC}=\frac{9 + 16-17}{2×3×4}=\frac{1}{3}$.又$0<\angle PCB<\pi$,所以$\sin\angle PCB=\sqrt{1-\cos^{2}\angle PCB}=\frac{2\sqrt{2}}{3}$.所以$\triangle PBC$的面积为$S=\frac{1}{2}PC· BC·\sin\angle PCB=\frac{1}{2}×3×4×\frac{2\sqrt{2}}{3}=4\sqrt{2}$.

解法2 分析:欲求$\triangle PBC$的面积,而已知$PC=3$,$BC=4$,则只需需求出$\triangle PBC$的边$PB$即可.又因为$\triangle POC(O$为对角线$AC$和$BD$的交点)可解,所以可借助关系式$\overrightarrow{PB}·\overrightarrow{PD}=\overrightarrow{PO}^{2}-\overrightarrow{OB}^{2}=\frac{PD^{2}+PB^{2}-BD^{2}}{2}$求出边$PB$的长.
如图,连接$AC$,$BD$交于点$O$,连接$PO$,则$O$为$AC$,$BD$的中点.在$\triangle POC$中,$PO^{2}=OC^{2}+PC^{2}-2OC· PC\cos\angle PCA=8 + 9-2×2\sqrt{2}×3×\frac{\sqrt{2}}{2}=5$,由$\overrightarrow{PB}·\overrightarrow{PD}=\overrightarrow{PO}^{2}-\overrightarrow{OB}^{2}=\frac{PD^{2}+PB^{2}-BD^{2}}{2}$,得$5-8=\frac{3^{2}+PB^{2}-32}{2}$,即$PB=\sqrt{17}$.在$\triangle PBC$中,$PC=3$,$PB=\sqrt{17}$,$BC=4$,所以$\cos\angle PCB=\frac{PC^{2}+BC^{2}-PB^{2}}{2PC· BC}=\frac{9 + 16-17}{2×3×4}=\frac{1}{3}$.又$0<\angle PCB<\pi$,所以$\sin\angle PCB=\sqrt{1-\cos^{2}\angle PCB}=\frac{2\sqrt{2}}{3}$.所以$\triangle PBC$的面积为$S=\frac{1}{2}PC· BC\sin\angle PCB=\frac{1}{2}×3×4×\frac{2\sqrt{2}}{3}=4\sqrt{2}$.

解后反思 解法1和解法2都是求边$PB$的长,但是选择的方法不同,解法1借助于基本事实:到线段两端点距离相等的点在线段的垂直平分面上,从而可得$PB=PA$,进而解三角形.解法2是根据$PO$是$\triangle PBD$的中线,借助向量数量积$\overrightarrow{PB}·\overrightarrow{PD}$的两种表示形式建立等式关系求解,当然也可以直接用二级结论:$(2PO)^{2}+DB^{2}=2(PB^{2}+PD^{2})$来求解边$PB$的长度.两种解法各有千秋,都需要掌握.
2. (2022 全国乙卷理,7)在正方体 $ ABCD - A_1B_1C_1D_1 $ 中, $ E,F $ 分别为 $ AB,BC $ 的中点,则 (
A.平面 $ B_1EF \perp $ 平面 $ BDD_1 $
B.平面 $ B_1EF \perp $ 平面 $ A_1BD $
C.平面 $ B_1EF // $ 平面 $ A_1AC $
D.平面 $ B_1EF // $ 平面 $ A_1C_1D $
A
)A.平面 $ B_1EF \perp $ 平面 $ BDD_1 $
B.平面 $ B_1EF \perp $ 平面 $ A_1BD $
C.平面 $ B_1EF // $ 平面 $ A_1AC $
D.平面 $ B_1EF // $ 平面 $ A_1C_1D $
答案:
2.A 解法1 因为$E$,$F$分别是$AB$,$BC$的中点,所以$EF// AC$,又因为四边形$ABCD$为正方形,所以$AC\perp BD$,从而$EF\perp BD$,由正方体可得$DD_{1}\perp$平面$ABCD$,从而$DD_{1}\perp EF$,又$BD\cap DD_{1}=D$,$BD,DD_{1}\subset$平面$BDD_{1}$,所以$EF\perp$平面$BDD_{1}$,又$EF\subset$平面$B_{1}EF$,所以平面$B_{1}EF\perp$平面$BDD_{1}$,故A正确;因为平面$A_{1}BD\cap$平面$BDD_{1}=BD$,由于平面$B_{1}EF\perp$平面$BDD_{1}$,故B错误;因为$AA_{1}$与$B_{1}E$必相交,所以平面$B_{1}EF$与平面$A_{1}AC$必有公共点,故C错误;由正方体可得平面$ACB_{1}//$平面$A_{1}C_{1}D$,而平面$B_{1}EF$与平面$ACB_{1}$有公共点,故$B_{1}EF$与平面$A_{1}C_{1}D$不可能平行,故D错误.
解法2 在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中,$AC\perp BD$且$DD_{1}\perp$平面$ABCD$,又$EF\subset$平面$ABCD$,所以$EF\perp DD_{1}$,因为$E$,$F$分别为$AB$,$BC$的中点,所以$EF// AC$,所以$EF\perp BD$,又$BD\cap DD_{1}=D$,$BD,DD_{1}\subset$平面$BDD_{1}$,所以$EF\perp$平面$BDD_{1}$,又$EF\subset$平面$B_{1}EF$,所以平面$B_{1}EF\perp$平面$BDD_{1}$,故A正确;如图,以$\{D\overrightarrow{A},D\overrightarrow{C},D\overrightarrow{D_{1}}\}$为正交基底,建立空间直角坐标系$D - xyz$,设$AB=2$,则$D(0,0,0)$,$B_{1}(2,2,2)$,$E(2,1,0)$,$F(1,2,0)$,$B(2,2,0)$,$A_{1}(2,0,2)$,$A(2,0,0)$,$C(0,2,0)$,$C_{1}(0,2,2)$,则$\overrightarrow{EF}=(-1,1,0)$,$\overrightarrow{EB_{1}}=(0,1,2)$,$\overrightarrow{DB}=(2,2,0)$,$\overrightarrow{DA_{1}}=(2,0,2)$,$\overrightarrow{AA_{1}}=(0,0,2)$,$\overrightarrow{AC}=(-2,2,0)$,$\overrightarrow{A_{1}C_{1}}=(-2,2,0)$,设平面$B_{1}EF$的法向量为$\mathbf{m}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\mathbf{m}·\overrightarrow{EF}=-x_{1}+y_{1}=0,\\\mathbf{m}·\overrightarrow{EB_{1}}=y_{1}+2z_{1}=0.\end{cases}$取$x_{1}=2$,则$y_{1}=2$,$z_{1}=-1$,得$\mathbf{m}=(2,2,-1)$,同理可得平面$A_{1}BD$的一个法向量为$\mathbf{n}_{1}=(1,-1,-1)$,平面$A_{1}AC$的一个法向量为$\mathbf{n}_{2}=(1,1,0)$,平面$A_{1}C_{1}D$的一个法向量为$\mathbf{n}_{3}=(1,1,-1)$,因为$\mathbf{m}·\mathbf{n}_{1}=2 - 2 + 1=1\neq0$,所以平面$B_{1}EF$与平面$A_{1}BD$不垂直,故B错误;因为$\mathbf{m}$与$\mathbf{n}_{2}$不平行,所以平面$B_{1}EF$与平面$A_{1}AC$不平行,故C错误;因为$\mathbf{m}$与$\mathbf{n}_{3}$不平行,所以平面$B_{1}EF$与平面$A_{1}C_{1}D$不平行,故D错误.

2.A 解法1 因为$E$,$F$分别是$AB$,$BC$的中点,所以$EF// AC$,又因为四边形$ABCD$为正方形,所以$AC\perp BD$,从而$EF\perp BD$,由正方体可得$DD_{1}\perp$平面$ABCD$,从而$DD_{1}\perp EF$,又$BD\cap DD_{1}=D$,$BD,DD_{1}\subset$平面$BDD_{1}$,所以$EF\perp$平面$BDD_{1}$,又$EF\subset$平面$B_{1}EF$,所以平面$B_{1}EF\perp$平面$BDD_{1}$,故A正确;因为平面$A_{1}BD\cap$平面$BDD_{1}=BD$,由于平面$B_{1}EF\perp$平面$BDD_{1}$,故B错误;因为$AA_{1}$与$B_{1}E$必相交,所以平面$B_{1}EF$与平面$A_{1}AC$必有公共点,故C错误;由正方体可得平面$ACB_{1}//$平面$A_{1}C_{1}D$,而平面$B_{1}EF$与平面$ACB_{1}$有公共点,故$B_{1}EF$与平面$A_{1}C_{1}D$不可能平行,故D错误.
解法2 在正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$中,$AC\perp BD$且$DD_{1}\perp$平面$ABCD$,又$EF\subset$平面$ABCD$,所以$EF\perp DD_{1}$,因为$E$,$F$分别为$AB$,$BC$的中点,所以$EF// AC$,所以$EF\perp BD$,又$BD\cap DD_{1}=D$,$BD,DD_{1}\subset$平面$BDD_{1}$,所以$EF\perp$平面$BDD_{1}$,又$EF\subset$平面$B_{1}EF$,所以平面$B_{1}EF\perp$平面$BDD_{1}$,故A正确;如图,以$\{D\overrightarrow{A},D\overrightarrow{C},D\overrightarrow{D_{1}}\}$为正交基底,建立空间直角坐标系$D - xyz$,设$AB=2$,则$D(0,0,0)$,$B_{1}(2,2,2)$,$E(2,1,0)$,$F(1,2,0)$,$B(2,2,0)$,$A_{1}(2,0,2)$,$A(2,0,0)$,$C(0,2,0)$,$C_{1}(0,2,2)$,则$\overrightarrow{EF}=(-1,1,0)$,$\overrightarrow{EB_{1}}=(0,1,2)$,$\overrightarrow{DB}=(2,2,0)$,$\overrightarrow{DA_{1}}=(2,0,2)$,$\overrightarrow{AA_{1}}=(0,0,2)$,$\overrightarrow{AC}=(-2,2,0)$,$\overrightarrow{A_{1}C_{1}}=(-2,2,0)$,设平面$B_{1}EF$的法向量为$\mathbf{m}=(x_{1},y_{1},z_{1})$,则$\begin{cases}\mathbf{m}·\overrightarrow{EF}=-x_{1}+y_{1}=0,\\\mathbf{m}·\overrightarrow{EB_{1}}=y_{1}+2z_{1}=0.\end{cases}$取$x_{1}=2$,则$y_{1}=2$,$z_{1}=-1$,得$\mathbf{m}=(2,2,-1)$,同理可得平面$A_{1}BD$的一个法向量为$\mathbf{n}_{1}=(1,-1,-1)$,平面$A_{1}AC$的一个法向量为$\mathbf{n}_{2}=(1,1,0)$,平面$A_{1}C_{1}D$的一个法向量为$\mathbf{n}_{3}=(1,1,-1)$,因为$\mathbf{m}·\mathbf{n}_{1}=2 - 2 + 1=1\neq0$,所以平面$B_{1}EF$与平面$A_{1}BD$不垂直,故B错误;因为$\mathbf{m}$与$\mathbf{n}_{2}$不平行,所以平面$B_{1}EF$与平面$A_{1}AC$不平行,故C错误;因为$\mathbf{m}$与$\mathbf{n}_{3}$不平行,所以平面$B_{1}EF$与平面$A_{1}C_{1}D$不平行,故D错误.

3. (多选题,2021 新高考Ⅰ卷,12)在正三棱柱 $ ABC - A_1B_1C_1 $ 中, $ AB = AA_1 = 1 $,点 $ P $ 满足 $ \overrightarrow{BP} = \lambda \overrightarrow{BC} + \mu \overrightarrow{BB_1} $,其中 $ \lambda \in [0,1] $,$ \mu \in [0,1] $,则 (
A.当 $ \lambda = 1 $ 时, $ \triangle AB_1P $ 的周长为定值
B.当 $ \mu = 1 $ 时,三棱锥 $ P - A_1BC $ 的体积为定值
C.当 $ \lambda = \frac{1}{2} $ 时,有且仅有一个点 $ P $,使得 $ A_1P \perp BP $
D.当 $ \mu = \frac{1}{2} $ 时,有且仅有一个点 $ P $,使得 $ A_1B \perp $ 平面 $ AB_1P $
BD
)A.当 $ \lambda = 1 $ 时, $ \triangle AB_1P $ 的周长为定值
B.当 $ \mu = 1 $ 时,三棱锥 $ P - A_1BC $ 的体积为定值
C.当 $ \lambda = \frac{1}{2} $ 时,有且仅有一个点 $ P $,使得 $ A_1P \perp BP $
D.当 $ \mu = \frac{1}{2} $ 时,有且仅有一个点 $ P $,使得 $ A_1B \perp $ 平面 $ AB_1P $
答案:
3.BD 对于A,如图1,当$\lambda=1$时,因为$\overrightarrow{BP}=\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,所以$\overrightarrow{CP}=\mu\overrightarrow{BB_{1}}$,此时点$P$在线段$CC_{1}$上运动,$\triangle AB_{1}P$的周长不为定值,故A错误.
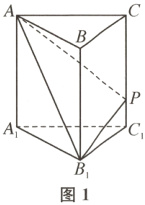
对于B,如图2,当$\mu=1$时,因为$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BB_{1}}$,所以$\overrightarrow{B_{1}P}=\lambda\overrightarrow{BC}$,此时点$P$在线段$B_{1}C_{1}$上运动.因为$B_{1}C_{1}// BC$,$B_{1}C_{1}\not\subset$平面$A_{1}BC$,$BC\subset$平面$A_{1}BC$,所以$B_{1}C_{1}//$平面$A_{1}BC$,则点$P$到平面$A_{1}BC$的距离就是$B_{1}C_{1}$到平面$A_{1}BC$的距离,为定值,所以$V_{三棱锥P - A_{1}BC}$为定值,故B正确.
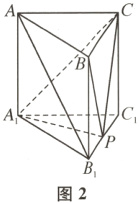
解法1(综合法) 对于C,如图3,当$\lambda=\frac{1}{2}$时,取$BC$,$B_{1}C_{1}$的中点分别为$E$,$F$,则$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}=\overrightarrow{BE}+\mu\overrightarrow{BB_{1}}$,所以$\overrightarrow{EP}=\mu\overrightarrow{BB_{1}}$,则点$P$在线段$EF$上运动.易知$A_{1}F\perp$平面$BB_{1}C_{1}C$,则$PF$为$A_{1}P$在平面$BB_{1}C_{1}C$内的射影.
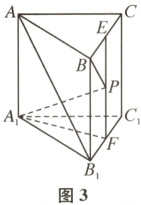
因为$A_{1}F\perp$平面$BB_{1}C_{1}C$,所以$A_{1}F\perp BP$.若$A_{1}P\perp BP$,又$A_{1}F\cap A_{1}P=A_{1}$,所以$BP\perp$平面$A_{1}FP$,所以$BP\perp PF$.当点$P$在点$E$位置时,满足题意;当点$P$在点$F$位置时,$A_{1}P$即为$A_{1}F$,又$A_{1}F\perp$平面$BB_{1}C_{1}C$,所以$A_{1}F\perp BF$.故有两个点$P$,故C错误.对于D,如图4,当$\mu=\frac{1}{2}$时,分别取$BB_{1}$,$CC_{1}$的中点为$M$,$N$,则$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_{1}}=\lambda\overrightarrow{BC}+\overrightarrow{BM}$,所以$\overrightarrow{MP}=\lambda\overrightarrow{BC}$,则点$P$在线段$MN$上运动.设$F$为$B_{1}C_{1}$的中点,则$A_{1}F\perp$平面$BB_{1}C_{1}C$,则$BF$为$A_{1}B$在平面$BB_{1}C_{1}C$内的射影.
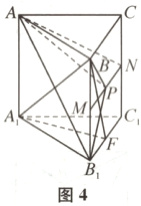
因为$A_{1}B\perp AB_{1}$,要使$A_{1}B\perp$平面$AB_{1}P$,只要$A_{1}B$在平面$BB_{1}C_{1}C$内的射影$BF$与$B_{1}P$垂直即可,故只有当点$P$与点$N$重合时,满足题意,故D正确.
解法2(空间向量法) 如图5,取$A_{1}C_{1}$的中点$O$,建立空间直角坐标系.
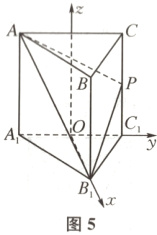
则$A_{1}\left(0,-\frac{1}{2},0\right)$,$A\left(0,-\frac{1}{2},1\right)$,$B_{1}\left(\frac{\sqrt{3}}{2},0,0\right)$,$B\left(\frac{\sqrt{3}}{2},0,1\right)$,$C_{1}\left(0,\frac{1}{2},0\right)$,$C\left(0,\frac{1}{2},1\right)$.设$P(x,y,z)$,则$\overrightarrow{BP}=\left(x-\frac{\sqrt{3}}{2},y,z - 1\right)$,$\overrightarrow{BC}=\left(-\frac{\sqrt{3}}{2},\frac{1}{2},0\right)$,$\overrightarrow{BB_{1}}=(0,0,-1)$.对于C,当$\lambda=\frac{1}{2}$时,$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,则有$\begin{cases}x-\frac{\sqrt{3}}{2}=-\frac{\sqrt{3}}{4},\\y=\frac{1}{4},\\z - 1=-\mu,\end{cases}$得$\begin{cases}x=\frac{\sqrt{3}}{4},\\y=\frac{1}{4},\\z=1-\mu,\end{cases}$则$\overrightarrow{A_{1}P}=\left(\frac{\sqrt{3}}{4},\frac{3}{4},1-\mu\right)$,$\overrightarrow{BP}=\left(-\frac{\sqrt{3}}{4},\frac{1}{4},-\mu\right)$.由$\overrightarrow{A_{1}P}·\overrightarrow{BP}=-\frac{3}{16}+\frac{3}{16}-\mu(1-\mu)=0$,所以$\mu=0$或$1$,满足题意的点$P$有两个,故C错误.对于D,当$\mu=\frac{1}{2}$时,$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_{1}}$,则有$\begin{cases}x-\frac{\sqrt{3}}{2}=-\frac{\sqrt{3}}{2}\lambda,\\y=\frac{1}{2}\lambda,\\z - 1=-\frac{1}{2},\end{cases}$得$\begin{cases}x=\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\lambda,\\y=\frac{1}{2}\lambda,\\z=\frac{1}{2},\end{cases}$则$\overrightarrow{B_{1}P}=\left(-\frac{\sqrt{3}}{2}\lambda,\frac{1}{2}\lambda,\frac{1}{2}\right)$.因为$A_{1}B\perp AB_{1}$,要使$A_{1}B\perp$平面$AB_{1}P$,只需$A_{1}B\perp B_{1}P$,又$\overrightarrow{A_{1}B}=\left(\frac{\sqrt{3}}{2},\frac{1}{2},1\right)$,所以$\overrightarrow{A_{1}B}·\overrightarrow{B_{1}P}=-\frac{3}{4}\lambda+\frac{\lambda}{4}+\frac{1}{2}=0$,所以$\lambda=1$,满足题意的点$P$只有$1$个,故D正确.
3.BD 对于A,如图1,当$\lambda=1$时,因为$\overrightarrow{BP}=\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,所以$\overrightarrow{CP}=\mu\overrightarrow{BB_{1}}$,此时点$P$在线段$CC_{1}$上运动,$\triangle AB_{1}P$的周长不为定值,故A错误.

对于B,如图2,当$\mu=1$时,因为$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\overrightarrow{BB_{1}}$,所以$\overrightarrow{B_{1}P}=\lambda\overrightarrow{BC}$,此时点$P$在线段$B_{1}C_{1}$上运动.因为$B_{1}C_{1}// BC$,$B_{1}C_{1}\not\subset$平面$A_{1}BC$,$BC\subset$平面$A_{1}BC$,所以$B_{1}C_{1}//$平面$A_{1}BC$,则点$P$到平面$A_{1}BC$的距离就是$B_{1}C_{1}$到平面$A_{1}BC$的距离,为定值,所以$V_{三棱锥P - A_{1}BC}$为定值,故B正确.

解法1(综合法) 对于C,如图3,当$\lambda=\frac{1}{2}$时,取$BC$,$B_{1}C_{1}$的中点分别为$E$,$F$,则$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}=\overrightarrow{BE}+\mu\overrightarrow{BB_{1}}$,所以$\overrightarrow{EP}=\mu\overrightarrow{BB_{1}}$,则点$P$在线段$EF$上运动.易知$A_{1}F\perp$平面$BB_{1}C_{1}C$,则$PF$为$A_{1}P$在平面$BB_{1}C_{1}C$内的射影.

因为$A_{1}F\perp$平面$BB_{1}C_{1}C$,所以$A_{1}F\perp BP$.若$A_{1}P\perp BP$,又$A_{1}F\cap A_{1}P=A_{1}$,所以$BP\perp$平面$A_{1}FP$,所以$BP\perp PF$.当点$P$在点$E$位置时,满足题意;当点$P$在点$F$位置时,$A_{1}P$即为$A_{1}F$,又$A_{1}F\perp$平面$BB_{1}C_{1}C$,所以$A_{1}F\perp BF$.故有两个点$P$,故C错误.对于D,如图4,当$\mu=\frac{1}{2}$时,分别取$BB_{1}$,$CC_{1}$的中点为$M$,$N$,则$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_{1}}=\lambda\overrightarrow{BC}+\overrightarrow{BM}$,所以$\overrightarrow{MP}=\lambda\overrightarrow{BC}$,则点$P$在线段$MN$上运动.设$F$为$B_{1}C_{1}$的中点,则$A_{1}F\perp$平面$BB_{1}C_{1}C$,则$BF$为$A_{1}B$在平面$BB_{1}C_{1}C$内的射影.

因为$A_{1}B\perp AB_{1}$,要使$A_{1}B\perp$平面$AB_{1}P$,只要$A_{1}B$在平面$BB_{1}C_{1}C$内的射影$BF$与$B_{1}P$垂直即可,故只有当点$P$与点$N$重合时,满足题意,故D正确.
解法2(空间向量法) 如图5,取$A_{1}C_{1}$的中点$O$,建立空间直角坐标系.

则$A_{1}\left(0,-\frac{1}{2},0\right)$,$A\left(0,-\frac{1}{2},1\right)$,$B_{1}\left(\frac{\sqrt{3}}{2},0,0\right)$,$B\left(\frac{\sqrt{3}}{2},0,1\right)$,$C_{1}\left(0,\frac{1}{2},0\right)$,$C\left(0,\frac{1}{2},1\right)$.设$P(x,y,z)$,则$\overrightarrow{BP}=\left(x-\frac{\sqrt{3}}{2},y,z - 1\right)$,$\overrightarrow{BC}=\left(-\frac{\sqrt{3}}{2},\frac{1}{2},0\right)$,$\overrightarrow{BB_{1}}=(0,0,-1)$.对于C,当$\lambda=\frac{1}{2}$时,$\overrightarrow{BP}=\frac{1}{2}\overrightarrow{BC}+\mu\overrightarrow{BB_{1}}$,则有$\begin{cases}x-\frac{\sqrt{3}}{2}=-\frac{\sqrt{3}}{4},\\y=\frac{1}{4},\\z - 1=-\mu,\end{cases}$得$\begin{cases}x=\frac{\sqrt{3}}{4},\\y=\frac{1}{4},\\z=1-\mu,\end{cases}$则$\overrightarrow{A_{1}P}=\left(\frac{\sqrt{3}}{4},\frac{3}{4},1-\mu\right)$,$\overrightarrow{BP}=\left(-\frac{\sqrt{3}}{4},\frac{1}{4},-\mu\right)$.由$\overrightarrow{A_{1}P}·\overrightarrow{BP}=-\frac{3}{16}+\frac{3}{16}-\mu(1-\mu)=0$,所以$\mu=0$或$1$,满足题意的点$P$有两个,故C错误.对于D,当$\mu=\frac{1}{2}$时,$\overrightarrow{BP}=\lambda\overrightarrow{BC}+\frac{1}{2}\overrightarrow{BB_{1}}$,则有$\begin{cases}x-\frac{\sqrt{3}}{2}=-\frac{\sqrt{3}}{2}\lambda,\\y=\frac{1}{2}\lambda,\\z - 1=-\frac{1}{2},\end{cases}$得$\begin{cases}x=\frac{\sqrt{3}}{2}-\frac{\sqrt{3}}{2}\lambda,\\y=\frac{1}{2}\lambda,\\z=\frac{1}{2},\end{cases}$则$\overrightarrow{B_{1}P}=\left(-\frac{\sqrt{3}}{2}\lambda,\frac{1}{2}\lambda,\frac{1}{2}\right)$.因为$A_{1}B\perp AB_{1}$,要使$A_{1}B\perp$平面$AB_{1}P$,只需$A_{1}B\perp B_{1}P$,又$\overrightarrow{A_{1}B}=\left(\frac{\sqrt{3}}{2},\frac{1}{2},1\right)$,所以$\overrightarrow{A_{1}B}·\overrightarrow{B_{1}P}=-\frac{3}{4}\lambda+\frac{\lambda}{4}+\frac{1}{2}=0$,所以$\lambda=1$,满足题意的点$P$只有$1$个,故D正确.
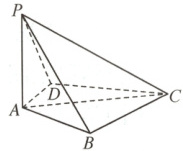
4. (2024 新高考Ⅰ卷,17)如图,在四棱锥 $ P - ABCD $ 中, $ PA \perp $ 底面 $ ABCD $, $ PA = AC = 2 $,$ BC = 1 $,$ AB = \sqrt{3} $.
(1) 若 $ AD \perp PB $,求证:$ AD // $ 平面 $ PBC $;
(2) 若 $ AD \perp DC $,且二面角 $ A - CP - D $ 的正弦值为$ \frac{\sqrt{42}}{7} $,求 $ AD $.
(1) 若 $ AD \perp PB $,求证:$ AD // $ 平面 $ PBC $;
(2) 若 $ AD \perp DC $,且二面角 $ A - CP - D $ 的正弦值为$ \frac{\sqrt{42}}{7} $,求 $ AD $.

答案:
4.
(1) 证明:因为$PA\perp$平面$ABCD$,$AD\subset$平面$ABCD$,所以$PA\perp AD$.又因为$AD\perp PB$,$PA\cap PB=P$,$PA,PB\subset$平面$PAB$,所以$AD\perp$平面$PAB$.因为$AB\subset$平面$PAB$,所以$AD\perp AB$.在$\triangle ABC$中,$AB^{2}+BC^{2}=AC^{2}$,所以$AB\perp BC$.因为$A$,$B$,$C$,$D$四点共面,所以$AD// BC$.又因为$BC\subset$平面$PBC$,$AD\not\subset$平面$PBC$,所以$AD//$平面$PBC$.
(2)解法1 以$DA$,$DC$所在直线分别为$x$轴和$y$轴,以过点$D$且垂直于平面$ABCD$的直线为$z$轴,建立如图所示的空间直角坐标系.设$AD=t$,则$DC=\sqrt{4-t^{2}}$,则$A(t,0,0)$,$P(t,0,2)$,$D(0,0,0)$,$C(0,\sqrt{4-t^{2}},0)$.设平面$ACP$的法向量为$\mathbf{m}=(x,y,z)$,$\overrightarrow{AC}=(-t,\sqrt{4-t^{2}},0)$,$\overrightarrow{AP}=(0,0,2)$,则$\begin{cases}\overrightarrow{AC}·\mathbf{m}=0,\\\overrightarrow{AP}·\mathbf{m}=0,\end{cases}$即$\begin{cases}-tx+\sqrt{4-t^{2}}y=0,\\2z=0,\end{cases}$可得$z=0$,取$y=t$,则$x=\sqrt{4-t^{2}}$,所以$\mathbf{m}=(\sqrt{4-t^{2}},t,0)$.设平面$CPD$的法向量为$\mathbf{n}=(a,b,c)$,$\overrightarrow{DC}=(0,\sqrt{4-t^{2}},0)$,$\overrightarrow{DP}=(t,0,2)$,则$\begin{cases}\overrightarrow{DC}·\mathbf{n}=0,\\\overrightarrow{DP}·\mathbf{n}=0,\end{cases}$即$\begin{cases}\sqrt{4-t^{2}}b=0,\\ta + 2c=0,\end{cases}$可得$b=0$,取$a=-2$,则$c=t$,所以$\mathbf{n}=(-2,0,t)$.因为二面角$A - CP - D$的正弦值为$\frac{\sqrt{42}}{7}$,所以其余弦值的绝对值为$\frac{\sqrt{7}}{7}$,则$\vert\cos\langle\mathbf{m},\mathbf{n}\rangle\vert=\frac{\vert\mathbf{m}·\mathbf{n}\vert}{\vert\mathbf{m}\vert\vert\mathbf{n}\vert}=\frac{\vert-2\sqrt{4-t^{2}}\vert}{2×\sqrt{t^{2}+4}}=\frac{\sqrt{7}}{7}$,解得$t=\sqrt{3}$,所以$AD=\sqrt{3}$.
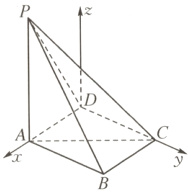
解法2 如图,过点$D$作$DO\perp AC$,垂足为$O$.因为$PA\perp$底面$ABCD$,$PA\subset$平面$PAC$,所以平面$PAC\perp$平面$ABCD$.又平面$PAC\cap$平面$ABCD=AC$,$DO\subset$平面$ABCD$,所以$DO\perp$平面$PAC$.因为$PC\subset$平面$PAC$,所以$DO\perp PC$.再过点$O$作$OG\perp PC$,垂足为$G$,连接$DG$.因为$DO\cap OG=O$,$DO,OG\subset$平面$DOG$,所以$PC\perp$平面$DOG$.又$DG\subset$平面$DOG$,所以$PC\perp DG$,所以$\angle DGO$为二面角$A - CP - D$的平面角.因为$DO\perp$平面$PAC$,$OG\subset$平面$PAC$,所以$DO\perp OG$,在$Rt\triangle DOG$中,$\sin\angle DGO=\frac{\sqrt{42}}{7}=\frac{DO}{DG}$①.在$Rt\triangle ADC$中,$AC=2$,设$AD=x$,则$DC=\sqrt{4-x^{2}}$,则$\frac{1}{2}AD· DC=\frac{1}{2}AC· DO$,所以$DO=\frac{AD· DC}{AC}=\frac{x·\sqrt{4-x^{2}}}{2}$②.因为$PA\perp$底面$ABCD$,$CD\subset$平面$ABCD$,所以$PA\perp CD$.又$AD\perp CD$,$PA\cap AD=A$,$PA,AD\subset$平面$PAD$,所以$CD\perp$平面$PAD$.又$PD\subset$平面$PAD$,所以$CD\perp PD$.因为$PA\perp$底面$ABCD$,$AD,AC\subset$平面$ABCD$,所以$PA\perp AD$,$PA\perp AC$.在$Rt\triangle PAD$中,$PD=\sqrt{PA^{2}+AD^{2}}=\sqrt{4+x^{2}}$.在$Rt\triangle PAC$中,$PC=\sqrt{PA^{2}+AC^{2}}=2\sqrt{2}$.在$Rt\triangle PDC$中,$\frac{1}{2}PD· DC=\frac{1}{2}PC· DG$,所以$DG=\frac{PD· DC}{PC}=\frac{\sqrt{4+x^{2}}·\sqrt{4-x^{2}}}{2\sqrt{2}}$③.将②③代入①,得$\frac{\sqrt{42}}{7}=\frac{\frac{x·\sqrt{4-x^{2}}}{2}}{\frac{\sqrt{4+x^{2}}·\sqrt{4-x^{2}}}{2\sqrt{2}}}$,即$\frac{x}{\sqrt{4+x^{2}}}=\frac{\sqrt{3}}{\sqrt{7}}$,解得$x=\sqrt{3}$,所以$AD=\sqrt{3}$.

4.
(1) 证明:因为$PA\perp$平面$ABCD$,$AD\subset$平面$ABCD$,所以$PA\perp AD$.又因为$AD\perp PB$,$PA\cap PB=P$,$PA,PB\subset$平面$PAB$,所以$AD\perp$平面$PAB$.因为$AB\subset$平面$PAB$,所以$AD\perp AB$.在$\triangle ABC$中,$AB^{2}+BC^{2}=AC^{2}$,所以$AB\perp BC$.因为$A$,$B$,$C$,$D$四点共面,所以$AD// BC$.又因为$BC\subset$平面$PBC$,$AD\not\subset$平面$PBC$,所以$AD//$平面$PBC$.
(2)解法1 以$DA$,$DC$所在直线分别为$x$轴和$y$轴,以过点$D$且垂直于平面$ABCD$的直线为$z$轴,建立如图所示的空间直角坐标系.设$AD=t$,则$DC=\sqrt{4-t^{2}}$,则$A(t,0,0)$,$P(t,0,2)$,$D(0,0,0)$,$C(0,\sqrt{4-t^{2}},0)$.设平面$ACP$的法向量为$\mathbf{m}=(x,y,z)$,$\overrightarrow{AC}=(-t,\sqrt{4-t^{2}},0)$,$\overrightarrow{AP}=(0,0,2)$,则$\begin{cases}\overrightarrow{AC}·\mathbf{m}=0,\\\overrightarrow{AP}·\mathbf{m}=0,\end{cases}$即$\begin{cases}-tx+\sqrt{4-t^{2}}y=0,\\2z=0,\end{cases}$可得$z=0$,取$y=t$,则$x=\sqrt{4-t^{2}}$,所以$\mathbf{m}=(\sqrt{4-t^{2}},t,0)$.设平面$CPD$的法向量为$\mathbf{n}=(a,b,c)$,$\overrightarrow{DC}=(0,\sqrt{4-t^{2}},0)$,$\overrightarrow{DP}=(t,0,2)$,则$\begin{cases}\overrightarrow{DC}·\mathbf{n}=0,\\\overrightarrow{DP}·\mathbf{n}=0,\end{cases}$即$\begin{cases}\sqrt{4-t^{2}}b=0,\\ta + 2c=0,\end{cases}$可得$b=0$,取$a=-2$,则$c=t$,所以$\mathbf{n}=(-2,0,t)$.因为二面角$A - CP - D$的正弦值为$\frac{\sqrt{42}}{7}$,所以其余弦值的绝对值为$\frac{\sqrt{7}}{7}$,则$\vert\cos\langle\mathbf{m},\mathbf{n}\rangle\vert=\frac{\vert\mathbf{m}·\mathbf{n}\vert}{\vert\mathbf{m}\vert\vert\mathbf{n}\vert}=\frac{\vert-2\sqrt{4-t^{2}}\vert}{2×\sqrt{t^{2}+4}}=\frac{\sqrt{7}}{7}$,解得$t=\sqrt{3}$,所以$AD=\sqrt{3}$.

解法2 如图,过点$D$作$DO\perp AC$,垂足为$O$.因为$PA\perp$底面$ABCD$,$PA\subset$平面$PAC$,所以平面$PAC\perp$平面$ABCD$.又平面$PAC\cap$平面$ABCD=AC$,$DO\subset$平面$ABCD$,所以$DO\perp$平面$PAC$.因为$PC\subset$平面$PAC$,所以$DO\perp PC$.再过点$O$作$OG\perp PC$,垂足为$G$,连接$DG$.因为$DO\cap OG=O$,$DO,OG\subset$平面$DOG$,所以$PC\perp$平面$DOG$.又$DG\subset$平面$DOG$,所以$PC\perp DG$,所以$\angle DGO$为二面角$A - CP - D$的平面角.因为$DO\perp$平面$PAC$,$OG\subset$平面$PAC$,所以$DO\perp OG$,在$Rt\triangle DOG$中,$\sin\angle DGO=\frac{\sqrt{42}}{7}=\frac{DO}{DG}$①.在$Rt\triangle ADC$中,$AC=2$,设$AD=x$,则$DC=\sqrt{4-x^{2}}$,则$\frac{1}{2}AD· DC=\frac{1}{2}AC· DO$,所以$DO=\frac{AD· DC}{AC}=\frac{x·\sqrt{4-x^{2}}}{2}$②.因为$PA\perp$底面$ABCD$,$CD\subset$平面$ABCD$,所以$PA\perp CD$.又$AD\perp CD$,$PA\cap AD=A$,$PA,AD\subset$平面$PAD$,所以$CD\perp$平面$PAD$.又$PD\subset$平面$PAD$,所以$CD\perp PD$.因为$PA\perp$底面$ABCD$,$AD,AC\subset$平面$ABCD$,所以$PA\perp AD$,$PA\perp AC$.在$Rt\triangle PAD$中,$PD=\sqrt{PA^{2}+AD^{2}}=\sqrt{4+x^{2}}$.在$Rt\triangle PAC$中,$PC=\sqrt{PA^{2}+AC^{2}}=2\sqrt{2}$.在$Rt\triangle PDC$中,$\frac{1}{2}PD· DC=\frac{1}{2}PC· DG$,所以$DG=\frac{PD· DC}{PC}=\frac{\sqrt{4+x^{2}}·\sqrt{4-x^{2}}}{2\sqrt{2}}$③.将②③代入①,得$\frac{\sqrt{42}}{7}=\frac{\frac{x·\sqrt{4-x^{2}}}{2}}{\frac{\sqrt{4+x^{2}}·\sqrt{4-x^{2}}}{2\sqrt{2}}}$,即$\frac{x}{\sqrt{4+x^{2}}}=\frac{\sqrt{3}}{\sqrt{7}}$,解得$x=\sqrt{3}$,所以$AD=\sqrt{3}$.

查看更多完整答案,请扫码查看


