2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第8页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
10. (多选题,2024 河南开封期末) 如图,在四棱锥 $ P - ABCD $ 中,底面 $ ABCD $ 是平行四边形,$ \overrightarrow{AP} = \boldsymbol{a} $,$ \overrightarrow{AB} = \boldsymbol{b} $,$ \overrightarrow{AD} = \boldsymbol{c} $。若 $ \overrightarrow{PE} = \overrightarrow{ED} $,$ \overrightarrow{CF} = 2\overrightarrow{FP} $,则 (
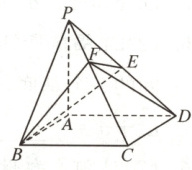
A.$ \overrightarrow{BE} = \frac{1}{2}\boldsymbol{a} - \boldsymbol{b} + \frac{1}{2}\boldsymbol{c} $
B.$ \overrightarrow{BF} = \frac{2}{3}\boldsymbol{a} + \frac{2}{3}\boldsymbol{b} - \frac{1}{3}\boldsymbol{c} $
C.$ \overrightarrow{DF} = \frac{2}{3}\boldsymbol{a} + \frac{1}{3}\boldsymbol{b} - \frac{2}{3}\boldsymbol{c} $
D.$ \overrightarrow{EF} = \frac{1}{6}\boldsymbol{a} - \frac{1}{3}\boldsymbol{b} + \frac{1}{6}\boldsymbol{c} $
AC
)
A.$ \overrightarrow{BE} = \frac{1}{2}\boldsymbol{a} - \boldsymbol{b} + \frac{1}{2}\boldsymbol{c} $
B.$ \overrightarrow{BF} = \frac{2}{3}\boldsymbol{a} + \frac{2}{3}\boldsymbol{b} - \frac{1}{3}\boldsymbol{c} $
C.$ \overrightarrow{DF} = \frac{2}{3}\boldsymbol{a} + \frac{1}{3}\boldsymbol{b} - \frac{2}{3}\boldsymbol{c} $
D.$ \overrightarrow{EF} = \frac{1}{6}\boldsymbol{a} - \frac{1}{3}\boldsymbol{b} + \frac{1}{6}\boldsymbol{c} $
答案:
10.AC $\overrightarrow{BE}=\overrightarrow{AE}-\overrightarrow{AB}=\frac{1}{2}(\overrightarrow{AP}+\overrightarrow{AD})-\overrightarrow{AB}=\frac{1}{2}a - b+\frac{1}{2}c$,故A正确;$\overrightarrow{BF}=\overrightarrow{AF}-\overrightarrow{AB}=\overrightarrow{AC}+\overrightarrow{CF}-\overrightarrow{AB}=\overrightarrow{AC}+\frac{2}{3}\overrightarrow{CP}-\overrightarrow{AB}=\frac{2}{3}\overrightarrow{AP}+\frac{1}{3}\overrightarrow{AC}-\overrightarrow{AB}=\frac{2}{3}a-\frac{2}{3}b+\frac{1}{3}c$,故B错误;$\overrightarrow{DF}=\overrightarrow{BF}-\overrightarrow{BD}=\frac{2}{3}a-\frac{2}{3}b+\frac{1}{3}c-(c - b)=\frac{2}{3}a+\frac{1}{3}b-\frac{2}{3}c$,故C正确;$\overrightarrow{EF}=\overrightarrow{BF}-\overrightarrow{BE}=(\frac{2}{3}a-\frac{2}{3}b+\frac{1}{3}c)-(\frac{1}{2}a - b+\frac{1}{2}c)=\frac{1}{6}a+\frac{1}{3}b-\frac{1}{6}c$,故D错误.
11. (2024 浙江金华期末) 如图,在四面体 $ ABCD $ 中,$ E, F, G, H $ 分别是 $ AB, BC, CD, DA $ 上的点,且 $ \frac{AE}{EB} = \frac{AH}{HD} = \frac{CF}{FB} = \frac{CG}{GD} = \frac{1}{2} $,$ M $ 是 $ EG $ 和 $ FH $ 的交点,以 $ \{\overrightarrow{AB}, \overrightarrow{AC}, \overrightarrow{AD}\} $ 为基底表示 $ \overrightarrow{AM} $,则 $ \overrightarrow{AM} = $

$\frac{1}{6}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}+\frac{1}{6}\overrightarrow{AD}$
.
答案:
11.$\frac{1}{6}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}+\frac{1}{6}\overrightarrow{AD}$ 因为$\frac{AE}{EB}=\frac{AH}{HD}=\frac{CF}{FG}=\frac{CG}{GD}=\frac{1}{2}$,所以$EH// BD$,$EH=\frac{1}{3}BD$.同理$FG// BD$,$FG=\frac{1}{3}BD$,所以$EH// FG$,$EH = FG$,故四边形$EFGH$为平行四边形,所以$\overrightarrow{AM}=\overrightarrow{AE}+\overrightarrow{EM}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{EG}=\frac{1}{3}\overrightarrow{AB}+\frac{1}{2}(\overrightarrow{EA}+\overrightarrow{AC}+\overrightarrow{CG})=\frac{1}{3}\overrightarrow{AB}-\frac{1}{6}\overrightarrow{AB}+\frac{1}{2}\overrightarrow{AC}+\frac{1}{6}(\overrightarrow{CA}+\overrightarrow{AD})=\frac{1}{6}\overrightarrow{AB}+\frac{1}{3}\overrightarrow{AC}+\frac{1}{6}\overrightarrow{AD}$.
12. (2023 湖北黄冈期末) 已知 $ \{\boldsymbol{a}, \boldsymbol{b}, \boldsymbol{c}\} $ 是空间的一个基底,$ \overrightarrow{OA} = 2\boldsymbol{a} + m\boldsymbol{b} + \boldsymbol{c} $,$ \overrightarrow{OB} = \boldsymbol{a} + 2\boldsymbol{b} $,$ \overrightarrow{OC} = \boldsymbol{a} + \boldsymbol{b} + \boldsymbol{c} $,已知点 $ O $ 在平面 $ ABC $ 内,则 $ m = $
3
.
答案:
12.3 因为点$O$在平面$ABC$内,所以$\overrightarrow{OA},\overrightarrow{OB},\overrightarrow{OC}$共面,所以存在实数$\lambda$与$\mu$,使得$\overrightarrow{OC}=\lambda\overrightarrow{OA}+\mu\overrightarrow{OB}$,即$a + b + c=\lambda(2a + mb + c)+\mu(a + 2b)= (2\lambda+\mu)a+(\lambda m + 2\mu)b+\lambda c$,所以$\begin{cases}2\lambda+\mu = 1,\\\lambda m + 2\mu = 1,\\\lambda = 1,\end{cases}$解得$\begin{cases}\lambda = 1,\\\mu = - 1,\\m = 3.\end{cases}$
13. (2024 广东中山开学考试) 如图,在平行六面体 $ ABCD - A_1B_1C_1D_1 $ 中,$ AB = 5 $,$ AD = 3 $,$ AA_1 = 4 $,$ \angle DAB = 90° $,$ \angle BAA_1 = \angle DAA_1 = 60° $,$ E $ 是 $ CC_1 $ 的中点。设 $ \overrightarrow{AB} = \boldsymbol{a} $,$ \overrightarrow{AD} = \boldsymbol{b} $,$ \overrightarrow{AA_1} = \boldsymbol{c} $。
(1) 求 $ AE $ 的长;
(2) 求异面直线 $ AE $ 和 $ BC $ 夹角的余弦值。

(1) 求 $ AE $ 的长;
(2) 求异面直线 $ AE $ 和 $ BC $ 夹角的余弦值。

答案:
13.解:
(1)由题意得$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CE}=a+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{CC_1}=a + b+\frac{1}{2}c$.
又$AB = 5$,$AD = 3$,$AA_1 = 4$,$\angle DAB = 90^{\circ}$,$\angle BAA_1=\angle DAA_1 = 60^{\circ}$,
故$\overrightarrow{AE}^2=(a + b+\frac{1}{2}c)^2=a^2 + b^2+\frac{1}{4}c^2+2a· b + b· c+a· c$
$=5^2 + 3^2+\frac{1}{4}×4^2+2|a|·|b|\cos90^{\circ}+|b|·|c|\cos60^{\circ}+|a|·|c|\cos60^{\circ}$
$=25 + 9 + 4+2×5×3×0+3×4×\frac{1}{2}+5×4×\frac{1}{2}$
$=25 + 9 + 4 + 6 + 10 = 54$,
故$AE = |\overrightarrow{AE}| = 3\sqrt{6}$.
(2)$\overrightarrow{AE}·\overrightarrow{BC}=(a + b+\frac{1}{2}c)· b=a· b + b^2+\frac{1}{2}c· b$
$=|a|·|b|\cos90^{\circ}+|b|^2+\frac{1}{2}|c|·|b|\cos60^{\circ}$
$=5×3×0+\frac{1}{2}×4×3×\frac{1}{2}=9 + 3 = 12$.
设异面直线$AE$和$BC$的夹角为$\theta$,
则$\cos\theta =|\cos\langle\overrightarrow{AE},\overrightarrow{BC}\rangle|=\frac{|\overrightarrow{AE}·\overrightarrow{BC}|}{|\overrightarrow{AE}|·|\overrightarrow{BC}|}=\frac{12}{3\sqrt{6}×3}=\frac{2\sqrt{6}}{9}$.
方法总结 用空间向量基本定理解决几何问题时需注意:
(1)若证明线线平行,则只需证明两向量共线.
(2)若证明线线垂直,则只需证明两向量的数量积为0.
(3)若求异面直线所成的角,则转化为求两向量的夹角.
(4)若求两点间的距离,则转化为求向量的模.
(1)由题意得$\overrightarrow{AE}=\overrightarrow{AB}+\overrightarrow{BC}+\overrightarrow{CE}=a+\overrightarrow{AD}+\frac{1}{2}\overrightarrow{CC_1}=a + b+\frac{1}{2}c$.
又$AB = 5$,$AD = 3$,$AA_1 = 4$,$\angle DAB = 90^{\circ}$,$\angle BAA_1=\angle DAA_1 = 60^{\circ}$,
故$\overrightarrow{AE}^2=(a + b+\frac{1}{2}c)^2=a^2 + b^2+\frac{1}{4}c^2+2a· b + b· c+a· c$
$=5^2 + 3^2+\frac{1}{4}×4^2+2|a|·|b|\cos90^{\circ}+|b|·|c|\cos60^{\circ}+|a|·|c|\cos60^{\circ}$
$=25 + 9 + 4+2×5×3×0+3×4×\frac{1}{2}+5×4×\frac{1}{2}$
$=25 + 9 + 4 + 6 + 10 = 54$,
故$AE = |\overrightarrow{AE}| = 3\sqrt{6}$.
(2)$\overrightarrow{AE}·\overrightarrow{BC}=(a + b+\frac{1}{2}c)· b=a· b + b^2+\frac{1}{2}c· b$
$=|a|·|b|\cos90^{\circ}+|b|^2+\frac{1}{2}|c|·|b|\cos60^{\circ}$
$=5×3×0+\frac{1}{2}×4×3×\frac{1}{2}=9 + 3 = 12$.
设异面直线$AE$和$BC$的夹角为$\theta$,
则$\cos\theta =|\cos\langle\overrightarrow{AE},\overrightarrow{BC}\rangle|=\frac{|\overrightarrow{AE}·\overrightarrow{BC}|}{|\overrightarrow{AE}|·|\overrightarrow{BC}|}=\frac{12}{3\sqrt{6}×3}=\frac{2\sqrt{6}}{9}$.
方法总结 用空间向量基本定理解决几何问题时需注意:
(1)若证明线线平行,则只需证明两向量共线.
(2)若证明线线垂直,则只需证明两向量的数量积为0.
(3)若求异面直线所成的角,则转化为求两向量的夹角.
(4)若求两点间的距离,则转化为求向量的模.
14. 如图,在平行六面体 $ ABCD - A'B'C'D' $ 中,$ E, F, G $ 分别是 $ A'D' $,$ DD' $,$ D'C' $ 的中点,请选择恰当的基底证明:
(1) $ EG // AC $;
(2) 平面 $ EFG // $ 平面 $ AB'C $。

(1) $ EG // AC $;
(2) 平面 $ EFG // $ 平面 $ AB'C $。

答案:
14.证明:取基底$\{\overrightarrow{AA^\prime},\overrightarrow{AB},\overrightarrow{AD}\}$.
(1)因为$\overrightarrow{EG}=\overrightarrow{ED}+\overrightarrow{DG}=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=2\overrightarrow{EG}$,所以$\overrightarrow{EG}//\overrightarrow{AC}$.
又$EG,AC$无公共点,所以$EG// AC$.
(2)因为$\overrightarrow{FG}=\overrightarrow{FD^\prime}+\overrightarrow{D^\prime G}=\frac{1}{2}\overrightarrow{AA^\prime}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AB^\prime}=\overrightarrow{AB}+\overrightarrow{AA^\prime}=2\overrightarrow{FG}$,所以$\overrightarrow{FG}//\overrightarrow{AB^\prime}$.
又$FG,AB^\prime$无公共点,所以$FG// AB^\prime$.
又$FG\not\subset$平面$AB^\prime C$,$AB^\prime\subset$平面$AB^\prime C$,所以$FG//$平面$AB^\prime C$.
由
(1)知$EG// AC$,又$EG\not\subset$平面$AB^\prime C$,$AC\subset$平面$AB^\prime C$,所以$EG//$平面$AB^\prime C$.
又$FG\cap EG = G$,$FG,EG\subset$平面$EFG$,所以平面$EFG//$平面$AB^\prime C$.
(1)因为$\overrightarrow{EG}=\overrightarrow{ED}+\overrightarrow{DG}=\frac{1}{2}\overrightarrow{AD}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AC}=\overrightarrow{AB}+\overrightarrow{AD}=2\overrightarrow{EG}$,所以$\overrightarrow{EG}//\overrightarrow{AC}$.
又$EG,AC$无公共点,所以$EG// AC$.
(2)因为$\overrightarrow{FG}=\overrightarrow{FD^\prime}+\overrightarrow{D^\prime G}=\frac{1}{2}\overrightarrow{AA^\prime}+\frac{1}{2}\overrightarrow{AB}$,$\overrightarrow{AB^\prime}=\overrightarrow{AB}+\overrightarrow{AA^\prime}=2\overrightarrow{FG}$,所以$\overrightarrow{FG}//\overrightarrow{AB^\prime}$.
又$FG,AB^\prime$无公共点,所以$FG// AB^\prime$.
又$FG\not\subset$平面$AB^\prime C$,$AB^\prime\subset$平面$AB^\prime C$,所以$FG//$平面$AB^\prime C$.
由
(1)知$EG// AC$,又$EG\not\subset$平面$AB^\prime C$,$AC\subset$平面$AB^\prime C$,所以$EG//$平面$AB^\prime C$.
又$FG\cap EG = G$,$FG,EG\subset$平面$EFG$,所以平面$EFG//$平面$AB^\prime C$.
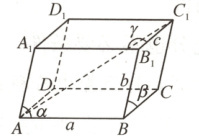
15. (2024 福建厦门阶段练习) 在自然界中,构成晶体的最基本的几何单元称为晶胞,其形状一般是平行六面体,具体形状大小由它的三组棱长 $ a, b, c $ 及棱间交角 $ \alpha, \beta, \gamma $(合称为“晶胞参数”)来确定。如图是某种晶体的晶胞,其中 $ a = 2 $,$ b = c = 1 $,$ \alpha = 60° $,$ \beta = 90° $,$ \gamma = 120° $,则该晶胞的体对角线 $ AC_1 $ 的长为
$\sqrt{10}$
.
答案:
15.$\sqrt{10}$ $\overrightarrow{AC_1}=\overrightarrow{AC}+\overrightarrow{CC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{CC_1}=\overrightarrow{AB}+\overrightarrow{AD}+\overrightarrow{AA_1}$.依题可知,$|\overrightarrow{AB}| = 2$,$|\overrightarrow{AA_1}| = |\overrightarrow{AD}| = 1$,$\alpha=\angle A_1AB = 60^{\circ}$,$\beta=\angle A_1AD = 90^{\circ}$,$\angle BAD = 180^{\circ}- \gamma = 60^{\circ}$,所以$|\overrightarrow{AC_1}|^2=|\overrightarrow{AB}|^2+|\overrightarrow{AD}|^2+|\overrightarrow{AA_1}|^2+2\overrightarrow{AB}·\overrightarrow{AD}+2\overrightarrow{AB}·\overrightarrow{AA_1}+2\overrightarrow{AD}·\overrightarrow{AA_1}=4 + 1+1+2×1×1\cos60^{\circ}+2×1×1\cos60^{\circ}+2×1×1\cos90^{\circ}=10$,故$AC_1 = |\overrightarrow{AC_1}| = \sqrt{10}$.
查看更多完整答案,请扫码查看


