2025年小题狂做高中数学选择性必修第二册苏教版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年小题狂做高中数学选择性必修第二册苏教版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第65页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
8. (2023 安徽滁州阶段调研)设随机变量$ X \sim B(3, p) $,$ D(X) = \frac{2}{3} $,且$ E(X) > 1 $。若 8 名党员中有$\frac{15p}{2}$名男党员,从这 8 人中选 4 名代表,记选出的代表中男党员人数为$ Y $,则$ P(Y = 3) = $(
A.$\frac{3}{7}$
B.$\frac{4}{7}$
C.$\frac{5}{7}$
D.$\frac{6}{7}$
A
)A.$\frac{3}{7}$
B.$\frac{4}{7}$
C.$\frac{5}{7}$
D.$\frac{6}{7}$
答案:
8.A 因为$X\sim B(3,p)$,$D(X)=\frac{2}{3}$,所以$3p(1-p)=\frac{2}{3}$,解
得$p=\frac{1}{3}$或$p=\frac{2}{3}$.又因为$E(X)=3p>1$,所以$p>\frac{1}{3}$,可得
$p=\frac{2}{3}$,则$\frac{15p}{2}=5$,所以$P(Y=3)=\frac{C_{5}^{3}C_{5}^{2}}{C_{10}^{4}}=\frac{3}{7}$.
得$p=\frac{1}{3}$或$p=\frac{2}{3}$.又因为$E(X)=3p>1$,所以$p>\frac{1}{3}$,可得
$p=\frac{2}{3}$,则$\frac{15p}{2}=5$,所以$P(Y=3)=\frac{C_{5}^{3}C_{5}^{2}}{C_{10}^{4}}=\frac{3}{7}$.
9. (多选题,2023 山东聊城期末)一箱儿童玩具中有 3 件一等品、2 件二等品,现从中不放回地任取 2 件进行检测。记随机变量$ X $为检测到的一等品的件数,则(
A.$ X $服从二项分布
B.$ P(X \geq 1) = \frac{9}{10} $
C.$ E(X) = \frac{6}{5} $
D.最有可能取得的$ X $为 1
BCD
)A.$ X $服从二项分布
B.$ P(X \geq 1) = \frac{9}{10} $
C.$ E(X) = \frac{6}{5} $
D.最有可能取得的$ X $为 1
答案:
9.BCD 由题意可知X的分布列为
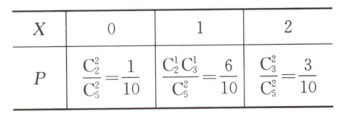
对于A,X服从超几何分布,而不是二项分布,故A错误;对于
B,$P(X\geq1)=1-P(X=0)=\frac{9}{10}$,故B正确;对于C,$E(X)=0×\frac{1}{10}+1×\frac{6}{10}+2×\frac{3}{10}=\frac{6}{5}$,故C正确;对于D,因为当X为1
时的概率最大,所以最有可能取得的X为1,故D正确.
9.BCD 由题意可知X的分布列为

对于A,X服从超几何分布,而不是二项分布,故A错误;对于
B,$P(X\geq1)=1-P(X=0)=\frac{9}{10}$,故B正确;对于C,$E(X)=0×\frac{1}{10}+1×\frac{6}{10}+2×\frac{3}{10}=\frac{6}{5}$,故C正确;对于D,因为当X为1
时的概率最大,所以最有可能取得的X为1,故D正确.
10. (多选题,2024 江苏靖江中学月考)袋中有 6 个大小相同的球,其中 4 个黑球、2 个白球。现从中任取 3 个球,记随机变量$ X $为其中白球的个数,随机变量$ Y $为其中黑球的个数。若取出一个白球得 2 分,取出一个黑球得 1 分,记随机变量$ Z $为取出 3 个球的总得分,则下列结论正确的是(
A.$ E(Y) = 2E(X) $
B.$ P(|Z - 5| \leq 1) = \frac{1}{5} $
C.$ E(Z) = 4 $
D.$ D(Z) = \frac{2}{5} $
ACD
)A.$ E(Y) = 2E(X) $
B.$ P(|Z - 5| \leq 1) = \frac{1}{5} $
C.$ E(Z) = 4 $
D.$ D(Z) = \frac{2}{5} $
答案:
10.ACD X,Y均服从超几何分布,且$X+Y=3$,$Z=2X+Y=3+X$,$P(X=k)=\frac{C_{2}^{k}C_{3}^{3-k}}{C_{6}^{3}}$,$k=0,1,2$.对于选项A,
$E(X)=\frac{3×2}{6}=1$,$E(Y)=3-E(X)=2=2E(X)$,故A正确;
对于选项B,$P(|Z-5|\leq1)=P(|X-2|\leq1)=1-P(X=0)=1-\frac{C_{3}^{3}}{C_{6}^{3}}=\frac{4}{5}$,故B错误;对于选项C,$E(Z)=3+E(X)=3+1=4$,故C正确;对于选项D,$D(Z)=D(3+X)=D(X)=E(X)·\frac{(6-2)×(6-3)}{6×(6-1)}=\frac{2}{5}$,故D正确.
方法总结 若离散型随机变量X服从参数为N,M,n的超几
何分布,则$D(X)=\frac{nM(N-M)(N-n)}{N^2(N-1)}=E(X)·\frac{(N-M)(N-n)}{N(N-1)}$
$E(X)=\frac{3×2}{6}=1$,$E(Y)=3-E(X)=2=2E(X)$,故A正确;
对于选项B,$P(|Z-5|\leq1)=P(|X-2|\leq1)=1-P(X=0)=1-\frac{C_{3}^{3}}{C_{6}^{3}}=\frac{4}{5}$,故B错误;对于选项C,$E(Z)=3+E(X)=3+1=4$,故C正确;对于选项D,$D(Z)=D(3+X)=D(X)=E(X)·\frac{(6-2)×(6-3)}{6×(6-1)}=\frac{2}{5}$,故D正确.
方法总结 若离散型随机变量X服从参数为N,M,n的超几
何分布,则$D(X)=\frac{nM(N-M)(N-n)}{N^2(N-1)}=E(X)·\frac{(N-M)(N-n)}{N(N-1)}$
11. 老师要从 10 篇课文中随机抽 3 篇让学生背,规定至少要背出 2 篇才能及格。同学甲只能背出其中的 6 篇,则甲同学能及格的概率为
设抽取的 3 篇课文中甲能背诵的课文有$ \xi $篇,则期望$ E(5\xi + 2) = $
$\frac{2}{3}$
;设抽取的 3 篇课文中甲能背诵的课文有$ \xi $篇,则期望$ E(5\xi + 2) = $
11
。
答案:
11.$\frac{2}{3}$依题意$\xi$可取0,1,2,3,且服从超几何分布.所以
$P(\xi=k)=\frac{C_{6}^{k}C_{4}^{3-k}}{C_{10}^{3}}(k=0,1,2,3)$,所以$\xi$的分布列为
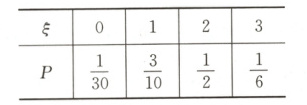
所以甲同学能及格的概率为$P(\xi\geq2)=P(\xi=2)+P(\xi=3)=\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$.随机变量$\xi$的期望$E(\xi)=0×\frac{1}{30}+1×\frac{3}{10}+2×\frac{1}{2}+3×\frac{1}{6}=\frac{9}{5}$,所以$E(5\xi+2)=5×\frac{9}{5}+2=11$.
11.$\frac{2}{3}$依题意$\xi$可取0,1,2,3,且服从超几何分布.所以
$P(\xi=k)=\frac{C_{6}^{k}C_{4}^{3-k}}{C_{10}^{3}}(k=0,1,2,3)$,所以$\xi$的分布列为

所以甲同学能及格的概率为$P(\xi\geq2)=P(\xi=2)+P(\xi=3)=\frac{1}{2}+\frac{1}{6}=\frac{2}{3}$.随机变量$\xi$的期望$E(\xi)=0×\frac{1}{30}+1×\frac{3}{10}+2×\frac{1}{2}+3×\frac{1}{6}=\frac{9}{5}$,所以$E(5\xi+2)=5×\frac{9}{5}+2=11$.
12. 3 月 5 日为“学雷锋纪念日”,某校将举行“弘扬雷锋精神,做全面发展一代新人”知识竞赛,某班现从 6 名女生和 3 名男生中选出 5 名学生参赛,要求每人回答一个问题,答对得 2 分,答错得 0 分。已知 6 名女生中有 2 人不会答所有题目,只能得 0 分,其余 4 人可得 2 分,3 名男生每人得 2 分的概率均为$\frac{1}{2}$,现选择 2 名女生和 3 名男生,每人答一题,则该班所选队员得分之和是 6 分的概率为
$\frac{43}{120}$
。
答案:
12.$\frac{43}{120}$依题意,该班所选队员得分之和为6分记为事件A,
则可分为下列三类:女生得0分、男生得6分,设为事件$A_1$;女
生得2分、男生得4分,设为事件$A_2$;女生得4分、男生得2分,
设为事件$A_3$.因为$P(A_1)=\frac{C_{2}^{2}× C_{3}^{3}(\frac{1}{2})^3}{C_{6}^{3}}=\frac{1}{120}$,$P(A_2)=\frac{C_{2}^{1}C_{3}^{2}×(\frac{1}{2})^3(\frac{1}{2})^2}{C_{6}^{3}}=\frac{1}{5}$,$P(A_3)=\frac{C_{2}^{2}C_{3}^{1}×(\frac{1}{2})^2(\frac{1}{2})^3}{C_{6}^{3}}=\frac{3}{20}$,所以$P(A)=P(A_1)+P(A_2)+P(A_3)=\frac{43}{120}$.
则可分为下列三类:女生得0分、男生得6分,设为事件$A_1$;女
生得2分、男生得4分,设为事件$A_2$;女生得4分、男生得2分,
设为事件$A_3$.因为$P(A_1)=\frac{C_{2}^{2}× C_{3}^{3}(\frac{1}{2})^3}{C_{6}^{3}}=\frac{1}{120}$,$P(A_2)=\frac{C_{2}^{1}C_{3}^{2}×(\frac{1}{2})^3(\frac{1}{2})^2}{C_{6}^{3}}=\frac{1}{5}$,$P(A_3)=\frac{C_{2}^{2}C_{3}^{1}×(\frac{1}{2})^2(\frac{1}{2})^3}{C_{6}^{3}}=\frac{3}{20}$,所以$P(A)=P(A_1)+P(A_2)+P(A_3)=\frac{43}{120}$.
13. (2024 江苏南京南航附中月考)为发展业务,某调研组对 A,B 两个公司的扫码支付情况进行调查,准备从国内$ n(n \in \mathbf{N}, n > 0) $个城区常住人口超过 1000 万的超大城市和 8 个城区常住人口低于 50 万的小城市中随机抽取若干个进行统计。若一次抽取 2 个城市,则全是小城市的概率为$\frac{4}{15}$。
(1) 求$ n $的值。
(2) 若一次抽取 4 个城市。
① 假设抽取的小城市的个数为$ X $,求$ X $的可能值及相应的概率;
② 若抽取的 4 个城市是同一类城市,求全为超大城市的概率。
(1) 求$ n $的值。
(2) 若一次抽取 4 个城市。
① 假设抽取的小城市的个数为$ X $,求$ X $的可能值及相应的概率;
② 若抽取的 4 个城市是同一类城市,求全为超大城市的概率。
答案:
13.解:
(1)从$(n+8)$个城市中一次抽取2个城市,有$C_{n+8}^{2}$种
情况,
其中全是小城市的有$C_{n}^{2}$种情况,则全是小城市的概率为
$\frac{C_{n}^{2}}{C_{n+8}^{2}}=\frac{8×7}{(n+8)(n+7)}=\frac{4}{15}$,
解得$n=7$(负值舍去).
(2)①由题意可知,X的可能取值为0,1,2,3,4,
$P(X=0)=\frac{C_{8}^{4}C_{7}^{0}}{C_{15}^{4}}=\frac{1}{39}$,$P(X=1)=\frac{C_{8}^{3}C_{7}^{1}}{C_{15}^{4}}=\frac{8}{39}$,
$P(X=2)=\frac{C_{8}^{2}C_{7}^{2}}{C_{15}^{4}}=\frac{28}{65}$,$P(X=3)=\frac{C_{8}^{1}C_{7}^{3}}{C_{15}^{4}}=\frac{56}{195}$,
$P(X=4)=\frac{C_{8}^{0}C_{7}^{4}}{C_{15}^{4}}=\frac{2}{39}$.
②若抽取的4个城市全是超大城市,共有$C_{3}^{4}=35$种情况;
若抽取的4个城市全是小城市,共有$C_{7}^{4}=70$种情况.
所以若抽取的4个城市是同一类城市,则全为超大城市的概率
为$\frac{35}{35+70}=\frac{1}{3}$.
(1)从$(n+8)$个城市中一次抽取2个城市,有$C_{n+8}^{2}$种
情况,
其中全是小城市的有$C_{n}^{2}$种情况,则全是小城市的概率为
$\frac{C_{n}^{2}}{C_{n+8}^{2}}=\frac{8×7}{(n+8)(n+7)}=\frac{4}{15}$,
解得$n=7$(负值舍去).
(2)①由题意可知,X的可能取值为0,1,2,3,4,
$P(X=0)=\frac{C_{8}^{4}C_{7}^{0}}{C_{15}^{4}}=\frac{1}{39}$,$P(X=1)=\frac{C_{8}^{3}C_{7}^{1}}{C_{15}^{4}}=\frac{8}{39}$,
$P(X=2)=\frac{C_{8}^{2}C_{7}^{2}}{C_{15}^{4}}=\frac{28}{65}$,$P(X=3)=\frac{C_{8}^{1}C_{7}^{3}}{C_{15}^{4}}=\frac{56}{195}$,
$P(X=4)=\frac{C_{8}^{0}C_{7}^{4}}{C_{15}^{4}}=\frac{2}{39}$.
②若抽取的4个城市全是超大城市,共有$C_{3}^{4}=35$种情况;
若抽取的4个城市全是小城市,共有$C_{7}^{4}=70$种情况.
所以若抽取的4个城市是同一类城市,则全为超大城市的概率
为$\frac{35}{35+70}=\frac{1}{3}$.
查看更多完整答案,请扫码查看


