《2025年小题狂做高中数学选择性必修第二册苏教版》

1. (2024辽宁丹东阶段练习)三个家庭的3位妈妈带着2名女宝和2名男宝共7人踏春，在沿着一条小溪行走时，为了安全起见，他们排队前进，3位母亲互不相邻照顾孩子，2名女宝相邻且不排最前面也不排最后面。为了防止2名男宝打闹，2人不相邻，且不排最前面也不排最后面，则不同的排法共有(D)

A.192种
B.288种
C.144种
D.96种

答案： 1. D 第一步，先将3名母亲全排，共有$A_3^3$种排法；第二步，将2名女宝“捆绑”在一起，共有$A_2^2$种排法；第三步，将“捆绑”在一起的2名女宝作为一个元素，在第一步形成的2个空中选择1个插入，有$A_2^1$种排法；第四步，先将2名男宝之中的一人，插入第三步后相邻的两个妈妈中间，然后将另一个男宝插入由女宝与两个妈妈形成的2个空中的其中1个，共有$C_2^1C_2^1$种排法.所以不同的排法有$A_3^3A_2^2A_2^1C_2^1C_2^1=96$种.

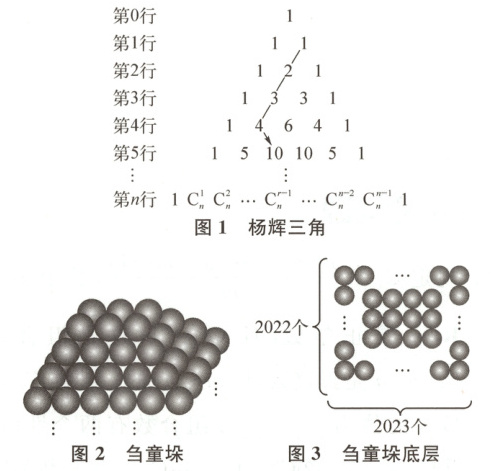
2. (2023吉林模拟)在我国古代，杨辉三角(如图1)是解决很多数学问题的有力工具，从图1中可以归纳出等式$ \mathrm{C}_{1}^{1}+\mathrm{C}_{2}^{1}+\mathrm{C}_{3}^{1}+·s+\mathrm{C}_{n}^{1}=\mathrm{C}_{n+1}^{2} $。类比上述结论，借助杨辉三角解决下述问题：
如图2，该“刍童垛”共2021层，底层如图3，一边2023个圆球，另一边2022个圆球，向上逐层每边减少1个圆球，顶层堆6个圆球，则此“刍童垛”中圆球的总数为(B)


A.$ 2\mathrm{C}_{2023}^{3}-2 $
B.$ 2\mathrm{C}_{2024}^{3}-2 $
C.$ \mathrm{C}_{2024}^{4}-2 $
D.$ \mathrm{C}_{2023}^{4}-2 $

答案： 2. B 从杨辉三角中观察可得$1 + 3 + 6 + 10 = 20$. 推广，得到$C_2^2 + C_3^2 + C_4^2 + ·s + C_{n+1}^2 = C_{n+2}^3$，即$\frac{1 × 2}{2} + \frac{2 × 3}{2} + \frac{3 × 4}{2} + ·s + \frac{n(n+1)}{2} = C_{n+2}^3$. 由题意，2021层“刍童垛”小球的总个数$S = 2 × 3 + 3 × 4 + 4 × 5 + ·s + 2022 × 2023 = 2(C_{2024}^3 - 1) = 2C_{2024}^3 - 2$.

3. (多选题，2024湖北武汉期中)下列说法正确的是(ACD)

A.将4个相同的小球放入3个不同的盒子中，要求不出现空盒，共有3种放法
B.$ 48^{2022}-3 $被7除后的余数为2
C.若$ (x+1)^{4}+(x-1)^{5}=a_{0}+a_{1}x+a_{2}x^{2}+a_{3}x^{3}+a_{4}x^{4}+a_{5}x^{5} $，则$ a_{0}+a_{2}+a_{4}=-8 $
D.10个朋友聚会，见面后每两个人握手一次，一共握手45次

答案： 3. ACD 对于A，选一个盒子放两个球，另外两个盒子放一个球，共有$C_3^1 = 3$种放法，故A正确；对于B，$48^{2022} - 3 = (49 - 1)^{2022} - 3 = 49^{2022} - C_{2022}^149^{2021} + C_{2022}^249^{2020} - ·s - C_{2022}^{2021}49 + C_{2022}^{2022} - 3 = 49^{2022} - C_{2022}^149^{2021} + C_{2022}^249^{2020} - ·s - C_{2022}^{2021}49 - 2$，展开式中只有最后一项$-2$不是7的倍数，所以$48^{2022} - 3$被7除后的余数为5，故B错误；对于C，在$(x + 1)^4 + (x - 1)^5 = a_0 + a_1x + a_2x^2 + a_3x^3 + a_4x^4 + a_5x^5$中，令$x = 1$，得$a_0 + a_1 + a_2 + a_3 + a_4 + a_5 = 2^4 = 16$，令$x = -1$，得$a_0 - a_1 + a_2 - a_3 + a_4 - a_5 = -2^5 = -32$，两式相加除以2，得$a_0 + a_2 + a_4 = -8$，故C正确；对于D，10个人两两握手，共有$C_{10}^2 = 45$次握手，故D正确.

4. (多选题，2024江苏苏州期末)对于$ a,d\in\mathrm{N}^{*} $，若$ \exists k\in\mathrm{N}^{*} $，使$ a=kd $，则称$ d $是$ a $的正因数，易知$ k $也是$ a $的正因数。正因数只有1与自身的数叫作素数，如2，3，5，7，11，……若对于正整数$ a $与$ b $，它们之间最大公因数为1，则称$ a $与$ b $互素。已知一个正整数可以被唯一分解为一组素数的乘积：$ n = p_{1}^{a_{1}}p_{2}^{a_{2}}·s p_{k}^{a_{k}} $，其中$ a_{i}\in\mathrm{N}^{*} $，$ p_{i} $是两两不同的素数，则下列说法正确的是(ACD)

A.从$ A=\{1,2,3,4,5,6,7\} $中随机取出两数，则它们互素的概率是$ \frac{17}{21} $
B.360的正因数个数为25
C.360的所有正因数之和为$ (2+1)^{3}(3+1)^{2}(5+1) $
D.360的所有正因数之积为$ 360^{12} $

答案： 4. ACD 对于A，从$A = \{1,2,3,4,5,6,7\}$中随机取出两数有$C_7^2 = 21$种取法，其中不互素的数组有$(2,4)$，$(2,6)$，$(4,6)$，$(3,6)$，共4种情况，所以它们互素的概率是$1 - \frac{4}{21} = \frac{17}{21}$，故A正确；对于B，因为$360 = 2^3 × 3^2 × 5^1$，所以360的正因数由2，3，5的乘积构成，其中2有4种取法，3有3种取法，5有2种取法，所以360的正因数个数为$4 × 3 × 2 = 24$，故B错误；对于C，由二项式定理可知360的正因数是$(2 + x)^3(3 + y)^2(5 + z)$展开式每一项的系数，令$x = y = z = 1$，所以360的所有正因数之和为$(2 + 1)^3(3 + 1)^2(5 + 1)$，故C正确；对于D，由题知，360的因数成对出现，共12对，每对的乘积都为360，所以360的所有正因数之积为$360^{12}$，故D正确.

5. (2024上海期中)用1，2，3，4，5组成没有重复数字的五位数$ abcde $，若满足$ a＞b＞c $且$ c＜d＜e $的五位数有$ n $个，则在$ 1+(1+x)^{1}+(1+x)^{2}+(1+x)^{3}+·s+(1+x)^{n+1} $的展开式中，$ x^{2} $的系数是56(用数字作答)。

答案： 5. 56 解法1 由五位数$abcde$满足$a ＞ b ＞ c$且$c ＜ d ＜ e$，得$c = 1$. 从2,3,4,5中任取两个分别作$a$，$b$，另两个为$d$，$e$，所以$n = C_4^2 = 6$，从而$1 + (1 + x)^1 + (1 + x)^2 + (1 + x)^3 + ·s + (1 + x)^{n + 1} = 1 + (1 + x)^1 + (1 + x)^2 + (1 + x)^3 + ·s + (1 + x)^7$的展开式中，$x^2$的系数为$C_2^2 + C_3^2 + C_4^2 + C_5^2 + C_6^2 + C_7^2 = C_3^3 + C_3^2 + C_4^2 + C_5^2 + C_6^2 + C_7^2 = C_4^3 + C_4^2 + C_5^2 + C_6^2 + C_7^2 = C_5^3 + C_5^2 + C_6^2 + C_7^2 = C_6^3 + C_6^2 + C_7^2 = C_7^3 + C_7^2 = C_8^3 = 56$.
解法2 由五位数$abcde$满足$a ＞ b ＞ c$且$c ＜ d ＜ e$，得$c = 1$. 从2,3,4,5中任取两个分别作$a$，$b$，另两个为$d$，$e$，所以$n = C_4^2 = 6$，从而$1 + (1 + x)^1 + (1 + x)^2 + (1 + x)^3 + ·s + (1 + x)^{n + 1} = 1 + (1 + x)^1 + (1 + x)^2 + (1 + x)^3 + ·s + (1 + x)^7 = \frac{1 - (1 + x)^8}{1 - (1 + x)} = \frac{(1 + x)^8 - 1}{x}$，所以它的展开式中$x^2$的系数为$\frac{(1 + x)^8}{x}$展开式中$x^3$的系数，即为$C_8^3 = 56$.

6. 现有三对双胞胎共6人排成一排，则有且只有一对双胞胎相邻的排法种数是288。

答案： 6. 288 将6人进行编号，分别为A，B，C，D，E，F，其中A，B为双胞胎，C，D为双胞胎，E，F为双胞胎，从左到右站位，分别为1,2,3,4,5,6，先从3对双胞胎中选择一对，令两人相邻，且两人可内部排列，故有$C_3^1A_2^2$种排法. 若这对双胞胎分别站在1,2位，此时3号位可以从剩余的4人中选择，则4号位可以从剩余的双胞胎中选择1人，5,6号位置将固定排剩余2人，此时共有$C_3^1A_2^2C_2^1C_2^1 = 48$种排法；若这对双胞胎分别站在2,3位，则1号位置有4种选择，4号位可以从剩余的双胞胎中选择1人，5,6位置将固定排剩余2人，此时共有$C_3^1A_2^2C_2^1C_2^1 = 48$种排法；若这对双胞胎分别站在3,4位，则2号位置有4种选择，1号位可以从剩余的双胞胎中选择1人，5,6位置可将剩余2人进行全排列，此时共有$C_3^1A_2^2C_2^1A_2^2 = 96$种排法；若这对双胞胎分别站在4,5或5,6位，可利用同种方法得到各有$C_3^1A_2^2C_2^1 = 48$种排法. 综上，共有$48 × 4 + 96 = 288$种排法.

7. (2024浙江嘉兴期中)已知二项式$ (x+3x^{2})^{n} $。
（1）若它的展开式的二项式系数之和为64，求展开式中系数最大的项；
（2）若$ x=1 $，$ n=31 $，求二项式的值被9除的余数。

答案： 7. 解：
(1) 由题意可知$2^n = 64$，解得$n = 6$，则$(x + 3x^2)^6$的展开式的通项为$T_{r + 1} = C_6^r x^{6 - r}(3x^2)^r = 3^rC_6^r x^{6 + r}(0 \leq r \leq 6,r \in \mathbf{N})$.
假设展开式中系数最大的项为第$r + 1$项，则$\begin{cases} 3^r · C_6^r \geq 3^{r - 1} · C_6^{r - 1}, \\ 3^r · C_6^r \geq 3^{r + 1} · C_6^{r + 1}. \end{cases}$即$\begin{cases} \frac{3 × 6!}{r!(6 - r)!} \geq \frac{6!}{(r - 1)!(7 - r)!}, \\ \frac{6!}{r!(6 - r)!} \geq \frac{3 × 6!}{(r + 1)!(5 - r)!}. \end{cases}$即$\begin{cases} \frac{3}{r} \geq \frac{1}{7 - r}, \\ \frac{1}{6 - r} \geq \frac{3}{r + 1}. \end{cases}$解得$\frac{17}{4} \leq r \leq \frac{21}{4}$，所以$r = 5$，所以展开式中系数最大的项为第6项，即$T_6 = 6 × 3^5x^{11} = 1458x^{11}$.
(2) 当$x = 1$，$n = 31$时，$(x + 3x^2)^n = 4^{31} = 2^{62} = 4 × 2^{60} = 4 × 8^{20} = 4 × [9^{20} + C_{20}^19^{19}(-1) + ·s + C_{20}^{19}9^1(-1)^{19} + (-1)^{20}] = 4 × [9^{20} + C_{20}^19^{19}(-1) + ·s + C_{20}^{19}9^1(-1)^{19}] + 4$，记$K = 9^{20} + C_{20}^19^{19}(-1) + ·s + C_{20}^{19}9^1(-1)^{19}$，显然$K$能被9整除，所以二项式的值被9除的余数为4.