《2025年小题狂做高中数学选择性必修第二册苏教版》

1. (2024 江苏连云港期中)已知向量$\boldsymbol{a}=(1,3,1)$，$\boldsymbol{b}=(2,1,1)$，$\boldsymbol{c}=(t,5,1)$共面，则实数$t$的值是(B)

A.$-1$
B.$0$
C.$1$
D.$2$

答案： 1. B 因为$a=(1,3,1),b=(2,1,1),c=(t,5,1)$三向量共面，所以存在实数$x,y$，使得$a=xb + yc$，所以$\begin{cases}1 = 2x + yt\\3 = x + 5y\\1 = x + y\end{cases}$，解得$\begin{cases}x=\frac{1}{2}\\y=\frac{1}{2}\\t = 0\end{cases}$。

2. (2025 宁夏银川阶段练习)如图，在正四棱台$ABCD - A_{1}B_{1}C_{1}D_{1}$中，$AB=2$，$A_{1}B_{1}=1$，则$\overrightarrow{AC_{1}}$在$\overrightarrow{AB}$上的投影向量是(A)

A.$\dfrac{3}{4}\overrightarrow{AB}$
B.$\dfrac{5}{6}\overrightarrow{AB}$
C.$\dfrac{3}{8}\overrightarrow{AB}$
D.$\dfrac{5}{8}\overrightarrow{AB}$

答案：
2. A 设正四棱台$ABCD - A_{1}B_{1}C_{1}D_{1}$的高为$h$，四边形$ABCD,A_{1}B_{1}C_{1}D_{1}$是正方形，设其中心分别为$F,E$，连接$CA$，$C_{1}A_{1}$，如图，以$F$为原点建立空间直角坐标系，且作$C_{1}G\perp CF$，由勾股定理得$CA = 2\sqrt{2},C_{1}A_{1}=\sqrt{2}$，所以$CF=\sqrt{2}$，$C_{1}E=\frac{\sqrt{2}}{2}$。由题意得$C_{1}E// CF,C_{1}G// EF$，所以四边形$EFGC_{1}$是平行四边形，所以$C_{1}E = GF=\frac{\sqrt{2}}{2},EF = C_{1}G$，故$CG=\frac{\sqrt{2}}{2}$。
所以$C_{1}(-\frac{1}{2},\frac{1}{2},h)$，而$A(1,-1,0),B(1,1,0)$，所以$\overrightarrow{AB}=(0,2,0),\overrightarrow{AC_{1}}=(-\frac{3}{2},\frac{3}{2},h)$，所以$\overrightarrow{AB}·\overrightarrow{AC_{1}}=2×\frac{3}{2}=3$。
由投影向量公式得$\overrightarrow{AC_{1}}$在$\overrightarrow{AB}$上的投影向量为$\frac{\overrightarrow{AB}·\overrightarrow{AC_{1}}}{|\overrightarrow{AB}|}·\frac{\overrightarrow{AB}}{|\overrightarrow{AB}|}=\frac{3}{4}\overrightarrow{AB}$。

3. (多选题，2024 江苏连云港期中)已知正方体$ABCD - A_{1}B_{1}C_{1}D_{1}$的棱长为$1$，动点$M$，$N$在对角线$AC$，$C_{1}D$上移动，且$\overrightarrow{AM}=\lambda \overrightarrow{AC}$，$\overrightarrow{DN}=\lambda \overrightarrow{DC_{1}}$，$\lambda \in (0,1)$，则下列结论正确的是(AB)

A.异面直线$AC$与$C_{1}D$所成的角为$60^{\circ}$
B.线段$MN$的最小值为$\dfrac{\sqrt{2}}{2}$
C.$MN$与平面$AA_{1}D_{1}D$不平行
D.存在$\lambda \in (0,1)$，使得$MN\perp AC$

答案：
3. AB 以$\{\overrightarrow{AB},\overrightarrow{AD},\overrightarrow{AA_{1}}\}$为正交基底，建立如图所示的空间直角坐标系$A - xyz$，则$A(0,0,0)$，$C(1,1,0),D(0,1,0),C_{1}(1,1,1)$，则$\overrightarrow{AC}=(1,1,0),\overrightarrow{DC_{1}}=(1,0,1)$。对于$A$选项，$\cos\langle\overrightarrow{AC},\overrightarrow{DC_{1}}\rangle=\frac{\overrightarrow{AC}·\overrightarrow{DC_{1}}}{|\overrightarrow{AC}||\overrightarrow{DC_{1}}|}=\frac{1}{\sqrt{2}×\sqrt{2}}=\frac{1}{2}$，又因为异面直线所成角的范围是$(0,\frac{\pi}{2}]$，所以异面直线$AC$与$C_{1}D$所成的角为$60^{\circ}$，故$A$正确；对于$B$选项，因为$\overrightarrow{AM}=\lambda\overrightarrow{AC}$，所以$\overrightarrow{AM}=(\lambda,\lambda,0)$，即$M(\lambda,\lambda,0)$，因为$\overrightarrow{DN}=\lambda\overrightarrow{DC_{1}}$，所以$\overrightarrow{DN}=(\lambda,0,\lambda),\overrightarrow{AN}=\overrightarrow{AD}+\overrightarrow{DN}=(0,1,0)+(\lambda,0,\lambda)=(\lambda,1,\lambda)$，故$N(\lambda,1,\lambda)$，所以$\overrightarrow{MN}=(0,1 - \lambda,\lambda)$，则$|\overrightarrow{MN}|=\sqrt{(1 - \lambda)^{2}+\lambda^{2}}=\sqrt{2\lambda^{2}-2\lambda + 1},\lambda\in(0,1)$，所以当$\lambda=\frac{1}{2}$时，$|\overrightarrow{MN}|$取得最小值$\frac{\sqrt{2}}{2}$，故$B$正确；对于$C$选项，由$\overrightarrow{AD}=(0,1,0),\overrightarrow{AA_{1}}=(0,0,1)$，得$\overrightarrow{MN}=(0,1 - \lambda,\lambda)=(1 - \lambda)\overrightarrow{AD}+\lambda\overrightarrow{AA_{1}}$，由空间向量共面定理知，$\overrightarrow{MN},\overrightarrow{AD},\overrightarrow{AA_{1}}$共面，又$MN\not\subset$平面$AA_{1}D_{1}D$，所以$MN//$平面$AA_{1}D_{1}D$，故$C$错误；对于$D$选项，若$MN\perp AC$，则$\overrightarrow{MN}·\overrightarrow{AC}=0×1 + 1×(1 - \lambda)+0×\lambda = 1 - \lambda = 0$，解得$\lambda = 1$，故不存在$\lambda\in(0,1)$，使得$MN\perp AC$，故$D$错误。

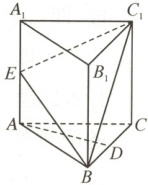
4. (2024 福建厦门期中)如图，在正三棱柱$ABC - A_{1}B_{1}C_{1}$中，$AB=2$，$AA_{1}=4$，$\overrightarrow{AE}=\lambda \overrightarrow{AA_{1}}$，$D$为$BC$的中点。当$AD//$平面$BC_{1}E$时，$\lambda =$$\frac{1}{2}$，此时，直线$AD$与直线$EC_{1}$所成的角的余弦值为$\frac{\sqrt{6}}{4}$。

答案：
4. $\frac{1}{2}$ $\frac{\sqrt{6}}{4}$ 因为$ABC - A_{1}B_{1}C_{1}$为正三棱柱，且$D$为$BC$的中点，取$B_{1}C_{1}$中点，连接$DD_{1}$，易得$DC$，$DA,DD_{1}$两两垂直，所以以$\{\overrightarrow{DC},\overrightarrow{DA},\overrightarrow{DD_{1}}\}$为正交基底，建立如图所示空间直角坐标系。因为$AB = 2,AA_{1}=4$，所以$D(0,0,0)$，$A(0,\sqrt{3},0),C(1,0,0),B(-1,0,0),A_{1}(0,\sqrt{3},4),C_{1}(1,0,4)$，则$\overrightarrow{AE}=\lambda\overrightarrow{AA_{1}}=(0,0,4\lambda)$，所以$E(0,\sqrt{3},4\lambda)$，则$\overrightarrow{BC_{1}}=(2,0,4),\overrightarrow{BE}=(1,\sqrt{3},4\lambda)$，设平面$BCE_{1}$的法向量为$\mathbf{n}=(x,y,z)$，则$\begin{cases}\overrightarrow{BC_{1}}·\mathbf{n}=2x + 4z = 0\\\overrightarrow{BE}·\mathbf{n}=x+\sqrt{3}y + 4\lambda z = 0\end{cases}$，取$z=\sqrt{3}$，则$x=-2\sqrt{3}$，所以平面$BCE_{1}$的一个法向量为$\mathbf{n}=(-2\sqrt{3},2 - 4\lambda,\sqrt{3})$。又$\overrightarrow{AD}=(0,-\sqrt{3},0)$，当$AD//$平面$BCE_{1}$时，$\mathbf{n}·\overrightarrow{AD}=-\sqrt{3}(2 - 4\lambda)=0$，解得$\lambda=\frac{1}{2}$，此时$\overrightarrow{EC_{1}}=(1,-\sqrt{3},2)$。设直线$AD$与直线$EC_{1}$所成的角为$\theta$，则$\cos\theta=|\cos\langle\overrightarrow{AD},\overrightarrow{EC_{1}}\rangle|=\frac{|\overrightarrow{AD}·\overrightarrow{EC_{1}}|}{|\overrightarrow{AD}||\overrightarrow{EC_{1}}|}=\frac{3}{\sqrt{3}×\sqrt{1 + 3 + 4}}=\frac{\sqrt{6}}{4}$，即直线$AD$与直线$EC_{1}$所成的角的余弦值为$\frac{\sqrt{6}}{4}$。

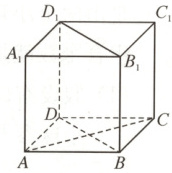
5. (2024 江苏宿迁期中)如图，直四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$的所有棱长都为$2$，$\angle BAD=\dfrac{\pi}{3}$，点$P$在四边形$BDD_{1}B_{1}$及其内部运动，且满足$PA+PC=4$，则点$P$到平面$AD_{1}B_{1}$的距离的最小值为$\frac{\sqrt{21}}{7}$。

答案：
5. $\frac{\sqrt{21}}{7}$ 设$BD,AC$交点为$O$，因为直四棱柱$ABCD - A_{1}B_{1}C_{1}D_{1}$的所有棱长都为$2,\angle BAD=\frac{\pi}{3}$，所以$BD\perp AC$，建立如图所示空间直角坐标系，所以$A(\sqrt{3},0,0),C(-\sqrt{3},0,0),D_{1}(0,-1,2),B_{1}(0,1,2),\overrightarrow{AD_{1}}=(-\sqrt{3},-1,2),\overrightarrow{AB_{1}}=(-\sqrt{3},1,2)$。设平面$AD_{1}B_{1}$的法向量为$\mathbf{n}=(x,y,z)$，则$\begin{cases}\mathbf{n}·\overrightarrow{AD_{1}}=-\sqrt{3}x - y + 2z = 0\\\mathbf{n}·\overrightarrow{AB_{1}}=-\sqrt{3}x + y + 2z = 0\end{cases}$，令$x = 2$，则$y = 0,z=\sqrt{3}$，所以$\mathbf{n}=(2,0,\sqrt{3})$。因为点$P$在四边形$BDD_{1}B_{1}$及其内部运动，所以设$P(0,y,z)(-1\leqslant y\leqslant1,0\leqslant z\leqslant2)$，又因为$PA + PC = 4$，所以$\sqrt{(-\sqrt{3})^{2}+y^{2}+z^{2}}+\sqrt{(\sqrt{3})^{2}+y^{2}+z^{2}} = 4$，即$y^{2}+z^{2}=1$，则$-1\leqslant y\leqslant1,0\leqslant z\leqslant1$。设点$P$到平面$AD_{1}B_{1}$的距离为$d$，则$d=\frac{|\overrightarrow{AP}·\mathbf{n}|}{|\mathbf{n}|}=\frac{|-\sqrt{3}×2+\sqrt{3}z|}{\sqrt{2^{2}+(\sqrt{3})^{2}}}=\frac{|\sqrt{3}z - 2\sqrt{3}|}{\sqrt{7}}$。又因为$0\leqslant z\leqslant1$，所以当$z = 1$时，$d_{min}=\frac{|\sqrt{3}-2\sqrt{3}|}{\sqrt{7}}=\frac{\sqrt{21}}{7}$，即点$P$到平面$AD_{1}B_{1}$的距离的最小值为$\frac{\sqrt{21}}{7}$。

1. (2023新高考Ⅱ卷，3)某学校为了了解学生参加体育运动的情况，用比例分配的分层随机抽样方法作抽样调查，拟从初中部和高中部共抽取60名学生，已知该校初中部和高中部分别有400名和200名学生，则不同的抽样结果共有(D)

A.$\mathrm{C}_{400}^{45}·\mathrm{C}_{200}^{15}$种
B.$\mathrm{C}_{400}^{20}·\mathrm{C}_{200}^{40}$种
C.$\mathrm{C}_{400}^{30}·\mathrm{C}_{200}^{30}$种
D.$\mathrm{C}_{400}^{40}·\mathrm{C}_{200}^{20}$种

答案： 1. D 按照分层抽样的规则，应从400名初中生中抽取40名，从200名高中生中抽取20名，则不同的抽样结果共有$C_{400}^{40} · C_{200}^{20}$种.

2. (2024全国甲卷文，4)甲、乙、丙、丁四人排成一列，则丙不在排头，且甲或乙在排尾的概率是(B)

A.$\frac{1}{4}$
B.$\frac{1}{3}$
C.$\frac{1}{2}$
D.$\frac{2}{3}$

答案：
2. B 解法1 画出树状图，如图:
　　　　
由树状图可得，甲、乙、丙、丁四人排成一列，共有24种排法，其中丙不在排头，且甲或乙在排尾的排法共有8种，故所求概率$P = \frac{8}{24} = \frac{1}{3}$.
解法2 当甲排在排尾，乙排在排头时，丙有2种排法，丁有1种，共2种；当甲排在排尾，乙排第二位或第三位时，丙有1种排法，丁有1种，共2种.故甲排在排尾共4种方法.同理乙排在排尾共4种方法，总共8种排法符合题意.基本事件总数为$A_{4}^{4} = 24$，根据古典概型的计算公式，丙不在排头，甲或乙在排尾的概率为$\frac{8}{24} = \frac{1}{3}$.

3. (2022新高考Ⅰ卷，13)$\left(1-\frac{y}{x}\right)(x + y)^8$的展
开式中，$x^2y^6$的系数为-28(用数字作答)。

答案： 3. -28 因为$(x + y)^{8}$的展开式的通项为$T_{r + 1} = C_{8}x^{8 - r}y^{r}$，$r = 0,1,·s,7,8$.令$r = 6$，得$T_{7} = C_{8}^{6}x^{2}y^{6}$，令$r = 5$，得$T_{6} = C_{8}^{5}x^{3}y^{5}$，所以$x^{2}y^{6}$的系数为$C_{8}^{6} - C_{8}^{5} = - 28$.

4. (2024全国甲卷理，13)$\left(\frac{1}{3}+x\right)^{10}$的展开式中，各项系数中的最大值为5。

答案： 4. 5 展开式的通项为$T_{r + 1} = C_{10}(\frac{1}{3})^{10 - r}x^{r},0 \leq r \leq 10$且$r \in Z$，设展开式中第$r + 1$项系数最大，则$\begin{cases} C_{10}(\frac{1}{3})^{10 - r} \geq C_{10}^{r + 1}(\frac{1}{3})^{9 - r}, \\ C_{10}(\frac{1}{3})^{10 - r} \geq C_{10}^{r - 1}(\frac{1}{3})^{11 - r}, \end{cases}$解得$\frac{29}{4} \leq r \leq \frac{33}{4}$.又$r \in Z$，故$r = 8$，所以展开式中系数最大的项是第9项，且该项的系数为$C_{10}^{8}(\frac{1}{3})^{2} = 5$.
解后反思 在二项展开式中的项数不太多时，此类题目可直接估算验证，如在$\frac{C_{10}^{r}}{3^{10 - r}}$中，当$r \leq 5$时，随着$r$的增大，分子在增大，分母在减小，其值逐渐增大，故只需比较$\frac{C_{10}^{8}}{3^{2}},\frac{C_{10}^{6}}{3^{4}},\frac{C_{10}^{7}}{3^{3}}$的大小，稍作计算(以估算为主)还是能得到$\frac{C_{10}^{8}}{3^{2}}$是最大的.

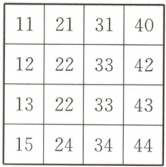
5. (2024新高考Ⅱ卷，14)在如图所示的$4×4$的方格表中选4个方格，要求每行和每列均恰有一个方格被选中，则共有24种选法；在所有符合上述要求的选法中，选中方格中的4个数之和的最大值是112。

答案：
5. 24 112 由题意知第一列有4个方格可选，第二列有3个方格可选，第三列有2个方格可选，第四列有1个方格可选，所以共有$4 × 3 × 2 × 1 = 24$种选法.由于每列数字的十位数均相同，分别为1,2,3,4，所以问题转化为在下列方格表中，选4个方格，且每行和每列均恰有一个方格被选中，选中方格中的4个数之和最大.
　　　　　　　　
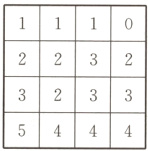
则选中满足条件的方格的4个数之和的最大值为$5 + 1 + 3 + 3 = 12$，所以在题目所给的方格表中，选中满足条件的方格的4个数之和的最大值为$100 + 12 = 112$.
解后反思 解决本题的关键是确定第一、二、三、四列分别有4,3,2,1个方格可选，运用分步计数原理可以顺利求解第一空.将各数和的最大值转化为个位数和的最大值，运用观察法不难求解第二空.