《2025年小题狂做高中数学选择性必修第二册苏教版》

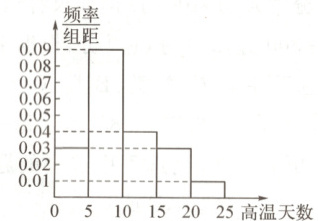
13. (2024安徽蚌埠阶段调研)在气象预报中,过往的统计数据至关重要.如图所示是根据甲地过去50年的气象记录所绘制的每年的高温天数(若某天气温达到$35^{\circ}C$及以上,则称之为高温天)的频率分布直方图.若某年的高温天数达到15天及以上,则称该年为高温年.假设每年是否为高温年相互独立,以这50年中每年高温天数的频率作为今后每年是否为高温年的概率.

(1) 求今后4年中,甲地至少有3年为高温年的概率.
(2) 某同学在位于甲地的大学里勤工俭学,成为校内奶茶店(消费区在户外)的店长,为了减少高温年带来的损失,该同学现在有两种方案选择.方案一:不购买遮阳伞,一旦某年为高温年,则预计当年的收入会减少6000元.方案二:购买一些遮阳伞,费用为5000元,可使用4年,一旦某年为高温年,则预计当年的收入会增加1000元.
以4年为期,试分析该同学是否应该购买遮阳伞.

答案： 13. 解：
(1) 由题意知某年为高温年的概率为 $(0.03 + 0.01) × 5 = 0.2$，设今后 4 年中高温年出现 $X$ 年，则 $X \sim B(4,0.2)$，所以 $P(X \geqslant 3)=P(X = 3)+P(X = 4)=C_4^3 × 0.2^3 × 0.8^1 + C_4^4 × 0.2^4 = 0.0272$. 故今后 4 年中，甲地至少有 3 年为高温年的概率是 0.0272.
(2) 若选择方案一，设今后 4 年共损失 $Y_1$ 元，则 $E(Y_1)=4 × 6000 × 0.2 = 4800$（元）；若选择方案二，设今后 4 年共损失 $Y_2$ 元，则 $E(Y_2)=5000 - 4 × 1000 × 0.2 = 4200$（元）. 因为 $E(Y_1)＞E(Y_2)$，所以该同学应该购买遮阳伞.

14. (2024江苏宿迁期中)高二(16)班参加青华中学红五月活动:猜歌名.班级只有一个名额,结合平时观察积累,甲、乙两名学生进入最后选拔.申老师为此设计了如下选拔方案:挑选8首歌进行测试,在这8首歌曲中,甲能正确说出其中6首歌名,乙能正确说出每首歌名的概率均为$\frac{3}{4}$.假设甲、乙两名学生说出每首歌名都相互独立、互不影响,现甲、乙从这8首歌中分别随机抽取4首进行竞猜.
(1) 求甲、乙共答对3首歌名的概率;
(2) 从数学期望和方差的角度分析,应选择哪个学生代表高二(16)班参加红五月活动?

答案： 14. 解：
(1) 设甲、乙答对的歌名数分别为 $X$，$Y$，则 $X$ 的值可能为 2，3，4，则 $P(X = 2)=\frac{C_4^2 C_6^2}{C_8^4}=\frac{3}{14}$，$P(X = 3)=\frac{C_4^3 C_6^1}{C_8^4}=\frac{4}{7}$，$P(X = 4)=\frac{C_4^4 C_6^0}{C_8^4}=\frac{3}{14}$. 由题意知，乙答对的歌名数满足 $Y \sim B(4,\frac{3}{4})$，故 $P(Y = 1)=C_4^1 × \frac{3}{4} × (\frac{1}{4})^3=\frac{3}{64}$，$P(Y = 0)=C_4^0 × (\frac{3}{4})^0 × (\frac{1}{4})^4=\frac{1}{256}$. 甲、乙共答对 3 首歌名，即甲答对 2 首，乙答对 1 首，或者甲答对 3 首，乙答对 0 首，故共答对 3 首歌名的概率 $P=\frac{3}{14} × \frac{3}{64} + \frac{4}{7} × \frac{1}{256}=\frac{11}{896}$.
(2) 由
(1)可知，甲答对的歌名数 $X$ 的分布列为
$X$ 2 3 4
$P$ $\frac{3}{14}$ $\frac{4}{7}$ $\frac{3}{14}$
故期望 $E(X)=2 × \frac{3}{14} + 3 × \frac{4}{7} + 4 × \frac{3}{14}=3$，
方差 $D(X)=(2 - 3)^2 × \frac{3}{14} + 0 + (4 - 3)^2 × \frac{3}{14}=\frac{3}{7}$.
又 $Y \sim B(4,\frac{3}{4})$，所以 $E(Y)=4 × \frac{3}{4}=3$，$D(Y)=4 × \frac{3}{4} × \frac{1}{4}=\frac{3}{4}$.
因为 $E(X)=E(Y)$，$D(X)＜D(Y)$.
所以甲、乙答对的歌名数期望一样，但是甲的方差更小，发挥更稳定，故应选择甲代表高二
(16)班参加红五月活动.

15. (2024广东佛山期末)甲、乙两位选手进行围棋比赛,设各局比赛的结果相互独立,且每局比赛甲获胜的概率为$p(0\lt p\lt1)$,乙获胜的概率为$1-p$.
(1) 若$p=0.4$,比赛采用三局两胜制,求甲获胜的概率;
(2) 若采用五局三胜制比采用三局两胜制对甲更有利,求$p$的取值范围;
(3) 若$p=0.6$,已知甲、乙进行了$n$局比赛且甲胜了11局,试给出$n$的估计值($X$表示$n$局比赛中甲胜的局数,以使得$P(X=11)$最大的$n$的值作为$n$的估计值).

答案： 15. 解：
(1) 若采用三局两胜制，则最终获胜的两种可能的比分为 $2:0$ 或 $2:1$.
因为每局比赛的结果是独立的，所以甲最终获胜的概率 $P = 0.4^2 + C_2^1 × 0.4 × 0.6 × 0.4 = 0.352$.
(2) 若采用五局三胜制，则甲最终获胜的三种可能的比分为 $3:0$，$3:1$ 或 $3:2$.
因为每局比赛的结果是独立的，所以甲最终获胜的概率 $P_1 = p^3 + C_3^2 × p^2 × (1 - p) × p + C_4^2 × p^2 × (1 - p)^2 × p = 10p^3 - 15p^4 + 6p^5$.
若采用三局两胜制，由
(1)可得甲最终获胜的概率 $P_2 = p^2 + C_2^1 × p × (1 - p) × p = 3p^2 - 2p^3$.
因为五局三胜制对甲更有利，所以 $P_1 ＞ P_2$，所以 $10p^3 - 15p^4 + 6p^5 ＞ 3p^2 - 2p^3$，即 $2p^3 - 5p^2 + 4p - 1 ＞ 0$，即 $(2p - 1)(p - 1)^2 ＞ 0$，解得 $\frac{1}{2} ＜ p ＜ 1$.
(3) 易得 $n \geqslant 11$，$X \sim B(n,p)$，$P(X = 11)=C_n^{11} p^{11} · (1 - p)^{n - 11}$，
记 $\frac{f(n + 1)}{f(n)}=\frac{C_{n + 1}^{11} p^{11} · (1 - p)^{(n + 1) - 11}}{C_n^{11} p^{11} · (1 - p)^{n - 11}}=\frac{\frac{(n + 1)!}{11!(n - 10)!} × \frac{2}{5}}{\frac{n!}{11!(n - 11)!} × \frac{2}{5}}=\frac{n + 1}{n - 10} × \frac{2}{5}$.
由 $\frac{f(n + 1)}{f(n)}=\frac{n + 1}{n - 10} × \frac{2}{5} ＞ 1$，得 $n \leqslant 17$，
即当 $11 \leqslant n \leqslant 17$ 时，$f(n) ＜ f(n + 1)$，当 $n \geqslant 18$ 时，$f(n) ＞ f(n + 1)$，
故当 $n = 18$ 时，$P(X = 11)$ 最大，所以 $n$ 的估计值为 18.