《2025年期末直通车七年级数学上册人教版》

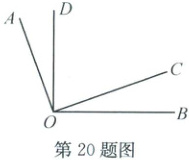
20. (8 分)如图,已知∠AOC = ∠BOD = 90°.
(1) 若∠BOC = 20°,求∠AOB 的度数.
(2) ∠COD 与∠AOB 互补吗? 请说明理由.

答案： 20.解：
(1)因为∠BOC=20°，∠AOC=90°，所以∠AOB=∠AOC+∠BOC=110°.
(2)∠COD与∠AOB互补.理由如下：设∠COD=x，因为∠BOD=90°，所以∠BOC=∠BOD-∠COD=90°-x.因为∠AOC=90°，所以∠AOB=∠BOC+∠AOC=90°-x+90°=180°-x，所以∠COD+∠AOB=x+180°-x=180°，所以∠COD与∠AOB互补.

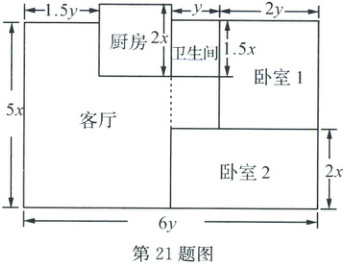
21. (8 分)如图是某住宅的平面结构示意图及有关尺寸(墙壁厚度忽略不计,单位:m).
(1) 求该住宅的面积(用含 x,y 的代数式表示).
(2) 该住宅的主人计划把卧室以外的地面都铺上地砖,其中卫生间的地面面积为 4.5 m². 如果地砖的价格是每平方米 80 元,那么购买地砖至少需要花费多少元?

答案： 21.解：
(1)根据示意图和尺寸，该住宅面积为$5x·6y+(2x-1.5x)·(6y-1.5y-y-2y)=30xy+0.75xy=30.75xy(m^{2}).$
(2)已知卫生间地面面积为$4.5m^{2}，$所以1.5xy=4.5，解得xy=3.该住宅卧室以外的面积为：$30.75xy-(5x-2x)·2y-2x·(y+2y)=30.75xy-6xy-6xy=18.75xy=18.75×3=56.25(m^{2})，$所以56.25×80=4500(元).
答：购买地砖至少需要花费4500元.

22. (10 分)观察下列三个等式:2 + 2 = 2×2,3 + $\frac{3}{2}$ = 3×$\frac{3}{2}$,$\frac{1}{2}$ + (-1) = $\frac{1}{2}$×(-1),我们将使等式 a + b = ab 成立的一对实数 a,b 称为“美好数对”,记为(a,b),例如数对(2,2),(3,$\frac{3}{2}$),($\frac{1}{2}$,-1)都是“美好数对”,请回答下列问题:
(1) 数对(-4,$\frac{4}{5}$)是“美好数对”吗? 请说明理由.(3 分)
(2) 若(a,$\frac{2}{3}$)是“美好数对”,求 a 的值.(3 分)
(3) 若(-3,m² - 2m)是“美好数对”,求代数式 m² - 2m 的值.(4 分)

答案： 22.解：
(1)是.理由如下：$-4+\frac{4}{5}=-\frac{16}{5}，$$-4×\frac{4}{5}=-\frac{16}{5}，$所以数对$(-4,\frac{4}{5})$满足$-4+\frac{4}{5}=-4×\frac{4}{5}，$符合“美好数对”定义，因此$(-4,\frac{4}{5})$是“美好数对”.
(2)根据“美好数对”定义，有$a+\frac{2}{3}=a×\frac{2}{3}，$解得a=-2.
(3)根据“美好数对”定义，有$-3+(m^{2}-2m)=-3×(m^{2}-2m).$移项，得$m^{2}-2m+3(m^{2}-2m)=3.$合并同类项，得$4(m^{2}-2m)=3.$两边同除以4，得$m^{2}-2m=\frac{3}{4}.$