第62页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
- 第72页
- 第73页
- 第74页
- 第75页
- 第76页
- 第77页
- 第78页
- 第79页
- 第80页
- 第81页
- 第82页
- 第83页
- 第84页
- 第85页
- 第86页
- 第87页
- 第88页
- 第89页
- 第90页
- 第91页
- 第92页
- 第93页
- 第94页
- 第95页
- 第96页
- 第97页
- 第98页
- 第99页
- 第100页
- 第101页
- 第102页
- 第103页
- 第104页
- 第105页
- 第106页
- 第107页
- 第108页
- 第109页
- 第110页
- 第111页
- 第112页
- 第113页
- 第114页
- 第115页
- 第116页
9. 已知实数$a,b$满足$|a-b|=-a-b$,且$a\neq b$,则下列说法中正确的是(
A.若$a=0$,则$a\lt b$
B.若$b=0$,则$a>b$
C.若$a>b$,则$a=0$
D.若$a\lt b$,则$a=0$
C
)A.若$a=0$,则$a\lt b$
B.若$b=0$,则$a>b$
C.若$a>b$,则$a=0$
D.若$a\lt b$,则$a=0$
答案:
9.C 解析:若a=0,则由$\vert a - b\vert=-\ a - b$,得$\vert b\vert=-b$,所以$b\leq0$,因为$a \neq b$,所以$a > b$,A不正确;若b=0,则由$\vert a - b\vert=-\ a - b$,得$\vert a\vert=-a$,所以$a\leq0$,因为$a \neq b$,所以$a < b$,B不正确;若$a > b$,则$\vert a - b\vert=a - b$,所以由$\vert a - b\vert=-\ a - b$,得$a - b=-\ a - b$,所以$a=0$,C正确;若$a < b$,则$\vert a - b\vert=b - a$,由$\vert a - b\vert=-\ a - b$,得$b - a=-\ a - b$,所以$b=0$,D不正确.故选C.
10. 将两张边长分别为$a$和$b$的正方形纸片按图示方式放置在长方形$ABCD$中. 若知道长方形$ABCD$的周长和两张正方形纸片重叠部分(阴影部分)的周长,则一定能求出(
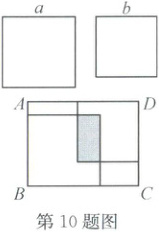
A.$a$
B.$b$
C.$a-b$
D.$a+b$
D
)
A.$a$
B.$b$
C.$a-b$
D.$a+b$
答案:
10.D 解析:设长方形ABCD周长为x,阴影部分周长为y,阴影部分长为p,宽为q,则由已知,易得$\begin{cases}AB + p=a + b,\\AD + q=a + b.\end{cases}$所以$(AB + AD)+(p + q)=2a + 2b$,即$\frac{1}{2}x + \frac{1}{2}y=2a + 2b$,故$a + b=\frac{1}{4}x + \frac{1}{4}y$.故选D.
11. 汽车在一条南北走向的高速公路上行驶,规定向北行驶为正. 汽车向南行驶6 km,记作
-6
km.
答案:
11.-6
12. 单项式$2a^{3}b^{2}c$的系数是
2
.
答案:
12.2
13. 若整数$m$满足$m<\sqrt{11}\lt m+1$,则$m$的值是
3
.
答案:
13.3
14. 如图,在长方形纸片$ABCD$中,点$E,F$分别在边$AD,BC$上. 现将纸片沿$EF$翻折,使点$D$落在点$D'$处,点$C$落在点$C'$处. 若$\angle AED'=98^{\circ}$,则$\angle D'EF$的度数是

41°
.
答案:
14.41°
15. 已知关于$x$的方程$x-\frac{x+2}{3}=\frac{3-a}{6}$的解为非负整数,请你写出一个符合条件的自然数$a$的值
3或7
.
答案:
15.3或7 解析:由$x - \frac{x + 2}{3}=\frac{3 - a}{6}$,得$4x=7 - a$.因为x为非负整数,所以$7 - a$为非负整数,且能被4整除,故a只能取3或7.
16. 如图是由10个不同的正整数组成的三角形数阵,其构造思路源于我国南宋数学家杨辉所著的《详解九章算法》一书中“杨辉三角”. 该三角形数阵从第二行开始,每一个数字都等于其上一行的左右两个数字之和. 例如:$a_{4}=a_{7}+a_{8},a_{5}=a_{8}+a_{9}$. 若$a_{1}=21$,则$a_{5}=$

4
.
答案:
16.4 解析:由题意,得$a_1 = a_2 + a_3=(a_4 + a_5)+(a_5 + a_6)=[(a_7 + a_8)+(a_8 + a_9)]+[(a_8 + a_9)+(a_9 + a_{10})]=(a_7 + a_8 + a_9 + a_{10})+2(a_8 + a_9)=21$,因为$2(a_8 + a_9)$为偶数,所以$a_7 + a_8 + a_9 + a_{10}$为奇数.因为这10个数均为互不相同的正整数,所以$(a_7 + a_8 + a_9 + a_{10})$最小为11,$(a_8 + a_9)$最小为3,记$a_7 + a_8 + a_9 + a_{10}=p$,$a_8 + a_9=q$,则$\begin{cases}p = 11,\\q = 5\end{cases}$或$\begin{cases}p = 13,\\q = 4\end{cases}$或$\begin{cases}p = 15,\\q = 3.\end{cases}$此时$\begin{cases}a_7 + a_{10}=6,\\a_8 + a_9=5\end{cases}$①或$\begin{cases}a_7 + a_{10}=9,\\a_8 + a_9=4\end{cases}$②或$\begin{cases}a_7 + a_{10}=12,\\a_8 + a_9=3.\end{cases}$③又因为$a_8 + a_9=a_5$,且这10个数各不相同,所以若为①,则没有满足的组合;若为②,则$a_8$,$a_9$为1,3,$a_7$,$a_{10}$为2,7;若为③,则$a_8$,$a_9$为1,2,$a_7$,$a_{10}$为4,8或5,7,由题意,易知当$a_7$,$a_8$,$a_9$,$a_{10}$分别为8,1,2,4(或4,1,2,8)和5,1,2,7(或7,1,2,5)时均会得到含重复数的10个正整数,故舍去.综上,只有当$a_7$,$a_8$,$a_9$,$a_{10}$分别为7,1,3,2(或2,3,1,7)时,满足题意,此时$a_5=4$.
查看更多完整答案,请扫码查看


