《2025年期末直通车七年级数学上册人教版》

8. 我国元代数学家朱世杰所著的《算学启蒙》中记载了这样一个问题:今有良马日行二百四十里,驽马日行一百五十里,驽马先行一十二日,问良马几何追及之. 大致意思为:跑得快的马每天走 240 里,跑得慢的马每天走 150 里. 慢马先走 12 天,快马几天可以追上慢马? 设快马 x 天可以追上慢马,则可列方程为(C)

A.240x = 150×12
B.240×12 = 150x
C.240x = 150(12 + x)
D.240(12 + x) = 150x

答案： 8.C

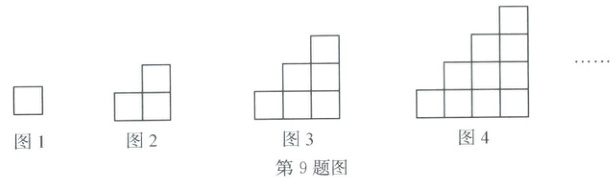
9. 如图,用大小相等的小正方形按照一定规律拼成以下一串图形. 图 1 用 1 个正方形,图 2 用 3 个正方形,图 3 用 6 个正方形……按照此规律,若图 n 中用的正方形个数比图 n - 2(n≥3)多 17 个,则 n 的值为(B)

A.7
B.9
C.10
D.12

答案： 9.B 解析：由所给图形可知，题图1中正方形的个数为1；题图2中正方形的个数为3=1+2；题图3中正方形的个数为6=1+2+3；…，所以图n中正方形的个数为：$1+2+3+…+n=\frac{n(n+1)}{2}。$因为图n中用的正方形个数比图$n-2(n\geq3)$多17个，所以$\frac{n(n+1)}{2}-\frac{(n-2)(n-1)}{2}=17，$解得n=9.故选B.

10. 已知∠1 与∠2 互为余角,∠1 与∠3 互为补角,有以下三个结论:①∠3 = 90° + ∠2;②∠3 = 2∠1 + ∠2;③∠3 - ∠1＞∠2. 其中正确的结论是(A)

A.①③
B.①
C.③
D.①②③

答案： 10.A 解析：由∠1+∠2=90°，∠1+∠3=180°，得∠3=180°-∠1=2(∠1+∠2)-∠1=∠1+2∠2，所以∠3＞∠1+∠2，所以②错误，③正确；因为∠1+∠2=90°，①∠1+∠3=180°，②所以②-①，得∠3=∠2+90°，所以①正确.故选A.

11. |-4| = 4.

答案： 11.4

12. -2a + 5a = 3a.

答案： 12.3a

13. 如图,点 C,D 在线段 AB 上,D 为 AB 的中点,AD = 3CD,若 CD = 2,则线段 BC 的长为8.

答案： 13.8

14. 若 x = 3 是关于 x 的方程 3x + 2a = 13 的解,则 a 的值是____.

答案： 14.2

15. 已知 a,n 均为正整数,若 n ＜ $\sqrt{10}$ ＜ n + 1,n - 1 ＜ $\sqrt{a}$ ＜ n,则 a 的最大值为8.

答案： 15.8 解析：由题意可知，$3＜\sqrt{10}＜4，$因此n=3.又因为$n-1＜\sqrt{a}＜n，$所以$2＜\sqrt{a}＜3.$由此可得4＜a＜9，由于a为正整数，所以a的最大值为8.故答案为8.

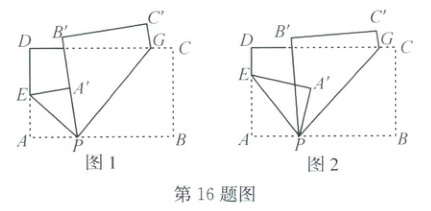
16. 一张矩形纸片 ABCD,若如图 1 翻折,点 A 的对应点 A'恰好落在 PB'上,折痕分别为 PE,PG,则∠EPG 的度数为90°. 若如图 2 翻折,点 A 的对应点 A'落在∠B'PG 的内部(不含角的两边),已知∠APE = 48°,∠A'PG = ∠EPB',则∠A'PB'的度数为12°.

答案： 16.90° 12° 解析：如题图1，因为点A的对应点A'恰好落在PB'上，折痕分别为PE，PG，所以∠A'PE=∠APE，∠B'PG=∠BPG，因为∠A'PE+∠APE+∠B'PG+∠BPG=180°，所以$∠EPG=∠A'PE+∠B'PG=\frac{1}{2}×180°=90°.$如题图2，由折叠的性质得出∠APE=∠A'PE，∠BPG=∠B'PG，因为∠APE=48°，所以∠A'PE=48°，即∠EPB'+∠A'PB'=48°，因为∠A'PG=∠EPB'，所以∠A'PG+∠A'PB'=∠EPB'+∠A'PB'，即∠A'PE=∠B'PG，所以∠APE=∠A'PE=∠B'PG=∠BPG=48°.因为∠APE+∠EPB'+∠B'PG+∠BPG=180°，即48°+∠EPB'+48°+48°=180°，所以∠EPB'=36°，所以∠A'PB'=∠A'PE-∠EPB'=48°-36°=12°.故答案为90° 12°.