《2025年期末直通车七年级数学上册人教版》

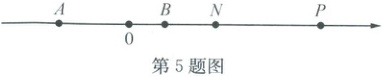
5. (2025·缙云改编)点A在数轴上对应的数为a，点B对应的数为b，且|a+4|+(b−2)²=0.如图，若点P是点B右侧一点，M为PA的中点，N为PB上靠近点B的三等分点.当点P在点B的右侧运动时，$\frac{1}{2}PM-\frac{3}{4}BN$的值为$\frac{3}{2}$.

答案： 5.$\frac{3}{2}$ 解析：由已知，易得$a = -4$，$b = 2$，所以$\frac{1}{2}PM-\frac{3}{4}BN=\frac{1}{4}PA-\frac{1}{4}PB=\frac{1}{4}AB=\frac{1}{4}[2-(-4)]=\frac{3}{2}$。

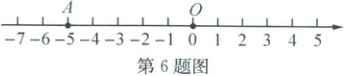
6. (2024·金华金东、兰溪、浦江)如图，已知数轴上点A表示的数为−5，点O表示的数为0.
(1)B是数轴上不与点A重合的点，且A,B两点间的距离为6个单位长度，则点B表示的数为1或-11.
(2)若有一只小乌龟从点A出发，以每分钟2个单位长度的速度向左匀速运动，有一只小白兔从原点O出发，以每分钟5个单位长度的速度向左匀速运动，但小白兔每走2分钟就要原地休息1分钟，小乌龟和小白兔同时出发，运动1或4分钟时，小乌龟和小白兔之间的距离为2个单位长度.

答案： 6.
(1)1或-11
(2)1或4 解析：
(2)小乌龟所在点表示的数为$-5 - 2t$，小白兔所在点表示的数为$-5t$，其中$t$在$0\sim2$，$3\sim5$，$6\sim8$，$9\sim11·s$时间内连续。在$0\sim2$分钟内，$|-5 - 2t + 5t| = 2$，解得$t = 1$或$\frac{7}{3}$(舍去)，在$3\sim5$分钟内，$|-5 - 2(t - 3)+5(t - 3)| = 2$，解得$t = 4$或$\frac{16}{3}$(舍去)，此后乌龟追不上兔子。故$t = 1$或$4$。

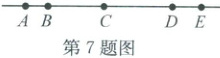
7. (2023·新昌)如图，在一条笔直的公路上依次有A,B,C,D,E五个站点.已知：AB=2千米，AD=13千米.站点维修工甲从B站匀速到E站进行维修，由于缺少零件，零件配送工乙带着零件从A站出发匀速追赶甲，他们同时出发，且在C站，乙追上了甲，将零件交给甲后，乙立即以原来的速度返回到A站.当乙到A站时，甲与D站的距离为3千米，则乙来回一共行驶了12或18千米.

答案： 7.12或18 解析：由题意，得甲从$B$站到$C$站与从$C$站到距离$D$站$3$千米处所花的时间相同，均为乙从$A$站到$C$站(或从$C$站到$A$站)所用的时间。①当甲到距离$D$站还差$3$千米处时，有$BC = CD - 3$。因为$AB = 2$千米，$AD = 13$千米，所以$BD = AD - AB = 11$(千米)，$CD = BD - BC = 11 - BC$，所以$BC = 11 - BC - 3$，解得$BC = 4$(千米)，所以$AC = AB + BC = 6$(千米)，所以$AC + CA = 2AC = 12$(千米)，所以乙来回一共行驶了$12$千米；②当甲到超过$D$站$3$千米处时，有$BC = CD + 3$，所以$BC = 11 - BC + 3$，解得$BC = 7$(千米)，所以$AC = 9$(千米)，$AC + CA = 18$(千米)，所以乙来回一共行驶了$18$千米。
综上，乙来回一共行驶了$12$千米或$18$千米。

8. (2025·丽水莲都)数轴上点A,B,C所表示的数分别是−2,6,x(x＞−2).
(1)求AB的长.
(2)若D是AB的中点，用含x的代数式表示CD的长.
(3)若点A以每秒5个单位长度的速度向左运动，同时，点B以每秒20个单位长度的速度向右运动，点C从原点开始以每秒1个单位长度的速度向右运动，记OB的中点为E，AC的中点为F，试通过计算说明$\frac{AB - OC}{EF}$的结果是定值.

答案： 8.解：
(1)$AB = 6-(-2)=8$。
(2)易知点$D$表示的数为$\frac{6+(-2)}{2}=2$，所以$CD = |x - 2|$。
(3)设运动时间为$t$，则点$A$表示的数为$-2 - 5t$，点$B$表示的数为$6 + 20t$，点$C$表示的数为$t$，所以点$E$表示的数为$3 + 10t$，点$F$表示的数为$\frac{-2 - 5t + t}{2}=-2t - 1$，所以$\frac{AB - OC}{EF}=\frac{|(-2 - 5t)-(6 + 20t)|-|t|}{|(3 + 10t)-(-2t - 1)|}=\frac{|25t + 8|-|t|}{|12t + 4|}=\frac{(25t + 8)-t}{12t + 4}=\frac{24t + 8}{12t + 4}=2$。