《2025年物理竞赛教程高中物理》

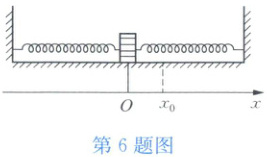
6 如图所示是放置在水平面上的两根完全相同的轻质弹簧与一个质量为$m$的物块组成的振子，每根弹簧的劲度系数均为$k$，弹簧的一端固定在墙上，另一端与物块相连，物块与水平面间的动摩擦因数和静摩擦因数均为$\mu$。当弹簧恰为原长时，物块位于$O$点。现将物块向右拉至$O$点右侧$x_{0}$处（未超过弹性限度），然后由静止释放。设弹簧在被压缩及拉长时一直保持在一条直线上，并规定物块从最右端运动至最左端（或从最左端运动至最右端）为一个振动过程。问：
（1）从释放到物块停止运动，物块经历了多少个振动过程？
（2）从释放到物块停止运动，物块共运动了多长时间？
（3）物块最后停在什么位置？
（4）整个过程中物块克服摩擦力做了多少功？

答案： （1）设$ N = \frac{k x_0}{\mu m g} $，振动过程数$ n = \left\lfloor N - \frac{1}{2} \right\rfloor $（$\lfloor · \rfloor$表示向下取整）
（2）每个振动过程时间为$ \pi \sqrt{\frac{m}{2k}} $，总时间$ t = n \pi \sqrt{\frac{m}{2k}} $
（3）停在距O点$ x = x_0 - (n + 1)\frac{\mu m g}{k} $处，方向与最后一次振动终点同向，且$ x \leq \frac{\mu m g}{2k} $
（4）克服摩擦力做功$ W = k(x_0^2 - x^2) $，其中$ x $为（3）中停止位置到O点的距离

7 两个劲度系数均为$k$、质量均为$m$的相同弹簧振子$1$、$2$置于光滑水平台面上，其固定端分别位于台面的两侧，两物块间又以劲度系数为$3k/2$的弹簧相连（如图）。现使两物块在台面上做同频率的简谐运动。试问此振动的频率为多少？

答案： 设两个弹簧振子的位移分别为$x_1$和$x_2$，弹簧的恢复力遵循胡克定律。
对于振子1：
$F_1 = -k x_1 + \frac{3k}{2} (x_2 - x_1)$。
化简得：$F_1 = -k x_1 + \frac{3k}{2} x_2 - \frac{3k}{2} x_1 = -\frac{5k}{2} x_1 + \frac{3k}{2} x_2$。
对于振子2：
$F_2 = -k x_2 + \frac{3k}{2} (x_1 - x_2)$。
化简得：$F_2 = -k x_2 + \frac{3k}{2} x_1 - \frac{3k}{2} x_2 = \frac{3k}{2} x_1 - \frac{5k}{2} x_2$。
假设解为：$x_1 = A_1 e^{i\omega t}, \quad x_2 = A_2 e^{i\omega t}$。
代入方程：
对于振子1：
$-\omega^2 m A_1 e^{i\omega t} = -\frac{5k}{2} A_1 e^{i\omega t} + \frac{3k}{2} A_2 e^{i\omega t}$。
化简得：$-\omega^2 m A_1 = -\frac{5k}{2} A_1 + \frac{3k}{2} A_2$。
对于振子2：
$-\omega^2 m A_2 e^{i\omega t} = \frac{3k}{2} A_1 e^{i\omega t} - \frac{5k}{2} A_2 e^{i\omega t}$。
化简得：$-\omega^2 m A_2 = \frac{3k}{2} A_1 - \frac{5k}{2} A_2$。
得到方程组：
$\begin{cases} (\frac{5k}{2} - \omega^2 m) A_1 - \frac{3k}{2} A_2 = 0 ,\\ -\frac{3k}{2} A_1 + (\frac{5k}{2} - \omega^2 m) A_2 = 0.\end{cases}$
令行列式为零以找到非零解：
$\begin{vmatrix} \frac{5k}{2} - \omega^2 m & -\frac{3k}{2} \\ -\frac{3k}{2} & \frac{5k}{2} - \omega^2 m \end{vmatrix} = 0$。
计算行列式：
$(\frac{5k}{2} - \omega^2 m)^2 - (\frac{3k}{2})^2 = 0$。
$(\frac{5k}{2} - \omega^2 m - \frac{3k}{2}) (\frac{5k}{2} - \omega^2 m + \frac{3k}{2}) = 0$。
解得：
$\omega^2 m = k \quad 或 \quad \omega^2 m = 4k$。
$\omega = \sqrt{\frac{k}{m}} \quad 或 \quad \omega = 2\sqrt{\frac{k}{m}}$。
频率$f$与角频率$\omega$的关系为：
$f = \frac{\omega}{2\pi}$。
因此，两个可能的振动频率为：
$f_1 = \frac{1}{2\pi} \sqrt{\frac{k}{m}}, \quad f_2 = \frac{1}{\pi} \sqrt{\frac{k}{m}}$。
所以，此振动频率为$\sqrt{\frac{k}{m}} /( 2\pi)$和$2\sqrt{\frac{k}{m}} /( 2\pi)$，即$\sqrt{\frac{k}{m}} /( 2\pi)$和$\sqrt{\frac{k}{m}} /( \pi)$。

8 一列平面简谐横波以$v = 50\mathrm{m}/\mathrm{s}$的速度沿$x$轴负方向传播，$t = 1\mathrm{s}$时的波形图如图所示。写出此波的波动方程，并绘出$t = 1\mathrm{s}$时各质元的速度与质元位置间的关系图像。

答案： 波动方程的一般形式为$y = A\sin(\omega t + \varphi + kx)$（波沿$x$轴负方向传播），由波形图可知振幅$A = 1.0\mathrm{cm}$。
从波形图可知波长$\lambda = 20\mathrm{m}$，根据$\omega=\frac{2\pi v}{\lambda}$（$v = 50\mathrm{m/s}$），可得$\omega=\frac{2\pi×50}{20}= 5\pi\mathrm{rad/s}$，波数$k=\frac{2\pi}{\lambda}=\frac{2\pi}{20}=\frac{\pi}{10}\mathrm{m}^{-1}$。
$t = 1\mathrm{s}$时，将$x = 0$代入波形图，$y = 0$，要满足波动方程，$\varphi = 0$。
所以波动方程为$y = 1.0\sin(5\pi t+\frac{\pi}{10}x)\mathrm{cm}$。
根据波沿$x$轴负方向传播，利用“同侧法”判断质元速度方向。
对波动函数求导得质元速度表达式$v_y=\frac{\partial y}{\partial t}= 5\pi×1.0\cos(5\pi t+\frac{\pi}{10}x)\mathrm{cm/s}$，$t = 1\mathrm{s}$时，$v_y = 5\pi\cos(\frac{\pi}{10}x + 5\pi)\mathrm{cm/s}=-5\pi\cos(\frac{\pi}{10}x)\mathrm{cm/s}$。
以$x$为横坐标，$v_y$为纵坐标，$x$取值范围可适当选取（如$0\leq x\leq20\mathrm{m}$），根据$v_y=-5\pi\cos(\frac{\pi}{10}x)$画出$t = 1\mathrm{s}$时各质元的速度与质元位置间的关系图像（为余弦函数图像）。

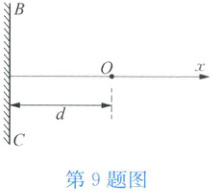
9 如图所示，原点$O$处有一波源，沿$x$轴向两边发射振幅为$A$、圆频率为$\omega$的简谐波，波速为$v$。$x = -d$处有一波密介质的反射面$BC$，入射波在此反射面发生完全反射。若$d = 5\lambda/4$（$\lambda$为波长）。求$x$轴上$x \geqslant -d$各处的波动方程。

答案： 分区间求解波动方程：
1. 求相关参数
波数 $ k = \frac{\omega}{v} $，波长 $ \lambda = \frac{2\pi v}{\omega} $，已知 $ d = \frac{5\lambda}{4} $。
2. 入射波与反射波表达式
入射波（O点向左传播，沿$-x$方向）：
$ y_1 = A\cos\left[\omega\left(t + \frac{x}{v}\right)\right] $（$ x \leq 0 $）。
反射波（反射面$ x=-d $反射后向右传播，沿$+x$方向）：
入射波在反射面$ x=-d $处振动：$ y_1(-d,t) = A\cos\left[\omega\left(t - \frac{d}{v}\right)\right] $。
波密介质反射有半波损失（相位突变$\pi$），反射波在$ x=-d $处振动：$ y_{反}(-d,t) = A\cos\left[\omega\left(t - \frac{d}{v}\right) + \pi\right] $。
反射波向右传播，波动方程为：
$ y_2 = A\cos\left[\omega\left(t - \frac{x + 2d}{v}\right) + \pi\right] $。
代入$ d = \frac{5\lambda}{4} $及$ \lambda = \frac{2\pi v}{\omega} $，化简得：$ y_2 = A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] $（$ x \geq -d $）。
3. 原向右传播的波（O点直接向右发射）
$ y_3 = A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] $（$ x \geq 0 $）。
4. 叠加结果
区间$ -d \leq x \leq 0 $：入射波$ y_1 $与反射波$ y_2 $叠加，
$ y = y_1 + y_2 = A\cos\left[\omega\left(t + \frac{x}{v}\right)\right] + A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] $。
由和差化积公式得：$ y = 2A\cos(\omega t)\cos\left(\frac{\omega x}{v}\right) $。
区间$ x \geq 0 $：反射波$ y_2 $与原向右波$ y_3 $叠加，
$ y = y_2 + y_3 = A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] + A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] = 2A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] $。
最终结论
当 $ -d \leq x \leq 0 $ 时，$ y = 2A\cos(\omega t)\cos\left(\frac{\omega x}{v}\right) $；
当 $ x \geq 0 $ 时，$ y = 2A\cos\left[\omega\left(t - \frac{x}{v}\right)\right] $。

10 如图所示，质量$M = 0.4\mathrm{kg}$的靶盒位于光滑水平导轨上，连接靶盒的弹簧的另一端与墙壁固定，弹簧的劲度系数$k = 200\mathrm{N}/\mathrm{m}$。当弹簧处于自然长度时，靶盒位于$O$点。$P$处有一固定的发射器，可以根据需要瞄准靶盒，每次发射出一颗水平速度$v_{0} = 50\mathrm{m}/\mathrm{s}$、质量$m = 0.10\mathrm{kg}$的球形子弹。当子弹打入靶盒后，便留在盒内（假定子弹与靶盒发生完全非弹性碰撞）。开始时靶盒静止。假设每当靶盒停在或到达$O$点时，都有一颗子弹打入靶盒内。
（1）若相继有$6$颗子弹打入靶盒，则每一颗子弹进入靶盒后，靶盒离开$O$点的最大距离各为多少？它从离开$O$点到回到$O$点经历的时间各为多少？
（2）若$P$点到$O$点的距离为$l = 0.25\mathrm{m}$，则至少要发射几颗子弹后停止射击，方能使靶盒来回运动而又不会碰到发射器？

答案： （1）每颗子弹打入后，靶盒离开O点的最大距离及往返时间如下：
n=1：$x_1=0.5\,m$，$t_1=0.05\pi\,s\approx0.157\,s$；
n=2：$x_2=\frac{5}{\sqrt{120}}\,m\approx0.456\,m$，$t_2=\pi\sqrt{\frac{0.6}{200}}\approx0.172\,s$；
n=3：$x_3=\frac{5}{\sqrt{140}}\,m\approx0.423\,m$，$t_3=\pi\sqrt{\frac{0.7}{200}}\approx0.186\,s$；
n=4：$x_4=\frac{5}{\sqrt{160}}\,m\approx0.395\,m$，$t_4=\pi\sqrt{\frac{0.8}{200}}\approx0.199\,s$；
n=5：$x_5=\frac{5}{\sqrt{180}}\,m\approx0.373\,m$，$t_5=\pi\sqrt{\frac{0.9}{200}}\approx0.211\,s$；
n=6：$x_6=\frac{5}{\sqrt{200}}\,m\approx0.353\,m$，$t_6=\pi\sqrt{\frac{1.0}{200}}\approx0.222\,s$。
（2）至少发射16颗子弹。