《2025年金版新学案高中数学选择性必修第二册北师大版》

1. (多选题) 若函数 $ f(x) $ 的导函数的部分图象如图所示，则 ( )


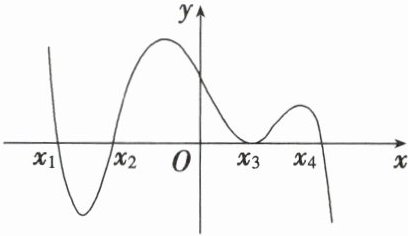
A.$ x_1 $ 是 $ f(x) $ 的一个极大值点
B.$ x_2 $ 是 $ f(x) $ 的一个极小值点
C.$ x_3 $ 是 $ f(x) $ 的一个极大值点
D.$ x_4 $ 是 $ f(x) $ 的一个极小值点

答案： AB 对于A，由图可知，在$x_1$左右两侧，函数$f(x)$左增右减，故$x_1$是$f(x)$的一个极大值点，故A正确；对于B，由图可知，在$x_2$附近的左右两侧，函数$f(x)$左减右增，故$x_2$是$f(x)$的一个极小值点，故B正确；对于C，由图可知，在$x_3$附近的左右两侧，函数$f(x)$单调递增，故$x_3$不是$f(x)$的一个极值点，故C错误；对于D，由图可知，在$x_4$左右两侧，函数$f(x)$左增右减，故$x_4$是$f(x)$的一个极大值点，故D错误.故选AB.

2. 已知 $ f(x) $ 在 $ \mathbf{R} $ 上连续可导，且 $ f'(x) $ 是 $ f(x) $ 的导数，$ p: f'(x_0) = 0 $，$ q: f(x) $ 在 $ x = x_0 $ 处取到极值，则 $ p $ 是 $ q $ 的 ( )

A.充分不必要条件
B.必要不充分条件
C.充要条件
D.既不充分也不必要条件

答案： B 依题意$f(x)$在$\mathbf{R}$上连续可导，且$f^{\prime}(x)$是$f(x)$的导数，$f^{\prime}(x_0) = 0$，则$x = x_0$不一定是极值点，$f(x)$在$x = x_0$处取到极值，则$f^{\prime}(x_0) = 0$，所以$p$是$q$的必要不充分条件.故选B.

3. (双空题) 函数 $ f(x) = \frac{1}{3}x^3 - x^2 - 3x + 6 $ 的极大值为________，极小值为________.

答案： $\frac{23}{3}$ $-3$ $f^{\prime}(x) = x^2 - 2x - 3$.令$f^{\prime}(x) ＞ 0$，得$x ＜ -1$或$x ＞ 3$；令$f^{\prime}(x) ＜ 0$得$-1 ＜ x ＜ 3$，故$f(x)$在$(-\infty, -1)$，$(3, +\infty)$上单调递增，在$(-1,3)$上单调递减，故$f(x)$的极大值为$f(-1) = \frac{23}{3}$，极小值为$f(3) = -3$.

4. 函数 $ f(x) = ax - 1 - \ln x(a \leq 0) $ 在定义域内的极值点的个数为________.

答案： 0 因为$x ＞ 0$，$f^{\prime}(x) = a - \frac{1}{x} = \frac{ax - 1}{x}$，所以当$a \leq 0$时，$f^{\prime}(x) ＜ 0$在$(0, +\infty)$上恒成立，所以函数$f(x)$在$(0, +\infty)$上单调递减，所以$f(x)$在$(0, +\infty)$上没有极值点.

同学们，上节课我们在群山之间穿梭，感受了每一个山峰与山谷的优美之处，而今天我们要寻找最高的山峰和最低的山谷，这其实就是我们今天要探究的函数的最值.
问题 如图为 $ y = f(x) $，$ x \in [a,b] $ 的图象.

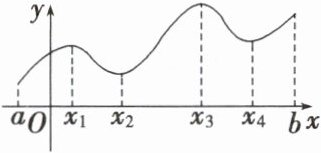
(1) 观察在区间 $[a,b]$ 上函数 $ y = f(x) $ 的图象，你能找出它的极大值、极小值吗？
(2) 结合图象判断，函数 $ y = f(x) $ 在区间 $[a,b]$ 上是否存在最大值，最小值？若存在，分别为多少？
(3) 函数 $ y = f(x) $ 在 $[a,b]$ 上的最大（小）值一定是某极值吗？

答案：
(1)极大值为$f(x_1),f(x_3)$，极小值为$f(x_2),f(x_4)$。
(2)存在，$f(x)_{min}=f(a),f(x)_{max}=f(x_3)$。
(3)不一定，也可能是区间端点的函数值。

1. 最值点
(1) 最大值点：函数 $ y = f(x) $ 在区间 $[a,b]$ 上的最大值点 $ x_0 $ 指的是：函数 $ f(x) $ 在这个区间上所有点处的函数值都 $$_________$ f(x_0)$.
(2) 最小值点：函数 $ y = f(x) $ 在区间 $[a,b]$ 上的最小值点 $ x_0 $ 指的是：函数 $ f(x) $ 在这个区间上所有点处的函数值都 $$_________$ f(x_0)$.

答案： 1.
(1)不超过
(2)不小于