《2025年金版新学案高中数学选择性必修第二册北师大版》

典例 3
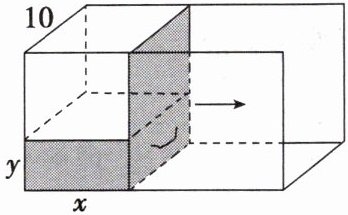
有一个长方体的容器，如图所示，它的宽为 $10\ cm$，高为 $100\ cm$，右侧面为一活塞，容器中装有 $1000\ mL$ 的水，活塞的初始位置（距左侧面）为 $x_0 = 1\ cm$，水面高度为 $100\ cm$. 当活塞位于距左侧面 $x\ cm$ 的位置时，水面高度为 $y\ cm$.
（1）写出 $y$ 关于 $x$ 的函数解析式；
（2）活塞的位置 $x$ 从 $1\ cm$ 变为 $2\ cm$，水面高度改变了多少？活塞的位置 $x$ 从 $8\ cm$ 变为 $10\ cm$，水面高度改变了多少？以上哪个过程水面高度的变化较快？
（3）试估计当 $x = 10\ cm$ 时，水面高度 $y$ 关于活塞位置 $x$ 的瞬时变化率.

答案： （1）因为$10xy = 1000$，所以$y = \frac{100}{x}$，即$y$关于$x$的函数解析式为$y = \frac{100}{x}(x \geq 1)$．（2）由（1）得$y = \frac{100}{x}$，设$y = f(x)$，则$f(x) = \frac{100}{x}$，所以$f(1) = 100,f(2) = 50,f(2) - f(1) = 50 - 100 = - 50(cm)$，所以活塞的位置$x$从$1\ cm$变为$2\ cm$水面高度改变了$-50\ cm$；$f(8) = 12.5,f(10) = 10$，则$f(10) - f(8) = 10 - 12.5 = - 2.5(cm)$；所以活塞的位置$x$从$8\ cm$变为$10\ cm$，水面高度改变了$-2.5\ cm$；因为$\frac{f(2) - f(1)}{2 - 1} = \frac{-50}{1} = - 50$，$\frac{f(10) - f(8)}{10 - 8} = \frac{-2.5}{2} = - 1.25$，且$\vert - 50\vert ＞ \vert - 1.25\vert$，故从$1\ cm$变为$2\ cm$，水面高度的变化较快．（3）因为$\frac{\Delta y}{\Delta x} = \frac{f(10 + \Delta x) - f(10)}{\Delta x} = \frac{\frac{100}{10 + \Delta x} - \frac{100}{10}}{\Delta x} = \frac{-10}{10 + \Delta x}$，当$\Delta x$趋于0时，$\frac{\Delta y}{\Delta x}$趋于$-1$，所以当$x = 10\ cm$时，水面高度$y$关于活塞位置$x$的瞬时变化率为$-1$．

已知某气球的体积 $V$（单位：$L$）与半径 $r$（单位：$dm$）之间的函数关系是 $V(r) = \frac{4}{3}\pi r^3$.
（1）求半径 $r$ 关于体积 $V$ 的函数 $r(V)$；
（2）分别求气球的体积 $V$ 从 $0\ L$ 增加到 $1\ L$ 和从 $1\ L$ 增加到 $2\ L$ 的过程中半径 $r$ 的平均变化率（精确到 $0.01$），并比较哪个过程中半径变化较快，此结论说明什么规律？
（注：$\sqrt[3]{\frac{3}{4\pi}} \approx 0.62$，$\sqrt[3]{\frac{3}{2\pi}} \approx 0.78$）

答案： （1）体积$V$(单位：L)与半径$r$(单位：dm)之间的函数关系是$V(r) = \frac{4}{3}\pi r^3$，即$V = \frac{4}{3}\pi r^3$，则$r^3 = \frac{3V}{4\pi}$，所以$r = \sqrt[3]{\frac{3V}{4\pi}}$，所以$r(V) = \sqrt[3]{\frac{3V}{4\pi}}$．（2）气球的体积$V$从$0\ L$增加到$1\ L$的过程中半径$r$的平均变化率：$\frac{r(1) - r(0)}{1 - 0} = \sqrt[3]{\frac{3×1}{4\pi}} - \sqrt[3]{\frac{3×0}{4\pi}} = \sqrt[3]{\frac{3}{4\pi}} \approx 0.62$，气球的体积$V$从$1\ L$增加到$2\ L$的过程中半径$r$的平均变化率：$\frac{r(2) - r(1)}{2 - 1} = \sqrt[3]{\frac{3×2}{4\pi}} - \sqrt[3]{\frac{3×1}{4\pi}} \approx 0.78 - 0.62 = 0.16$，可以看出，气球的体积$V$从$0\ L$增加到$1\ L$的过程中，半径变化较快．此结论说明随着气球的体积逐渐变大，气球的半径增加得越来越慢．

1. 在求解平均变化率时，自变量的变化量 $\Delta x$ 应满足( )

A.$\Delta x ＞ 0$
B.$\Delta x ＜ 0$
C.$\Delta x \neq 0$
D.$\Delta x$ 可为任意实数

答案： 1.C

2. 若函数 $y = \frac{1}{x}$ 在 $[1, a]$ 上的平均变化率为 $-\frac{1}{2}$，则 $a$ 等于( )

A.$1$
B.$2$
C.$3$
D.$4$

答案： 2.B

3. 已知函数 $f(x) = x^3$，则用平均变化率估计 $f(x)$ 在 $x = 1$ 处的瞬时变化率为( )

A.$1$
B.$2$
C.$3$
D.$4$

答案： 3.C

4. 一质点运动规律是 $s = t^2 + 3$($s$ 的单位为 $m$，$t$ 的单位为 $s$)，则该质点在 $t = 1\ s$ 时的瞬时速度估计是 __________ $m/s$.

答案： 4.2