2025年新坐标同步练习高中化学选择性必修第二册人教版青海专版
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年新坐标同步练习高中化学选择性必修第二册人教版青海专版 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
第60页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
4. (2024·广西卷) $KMnF_{3}$ 立方晶胞如右图所示,晶胞参数为 $a\ pm$,该晶体中与一个 $F^{-}$ 紧邻的 $K^{+}$ 有 $\underline{

4
}$ 个。已知 $N_{A}$ 为阿伏加德罗常数的值,晶体密度为 $\underline{$\frac{151}{N_{A}a^{3}×10^{-30}}$
}\ g·cm^{-3}$(用含 $a$、$N_{A}$ 的代数式表示)。
答案:
4 $\frac{151}{N_{A}a^{3}×10^{-30}}$
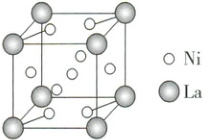
5. (1) 某镍镧合金是优质储氢材料,其晶胞如下图所示,该镍镧合金的化学式为
(2) 金属铬的晶胞结构如右图所示,已知晶体密度为 7.2 g/cm³,晶体中铬原子的半径为

(3) 金属铜与铝可形成多种组成不同的合金,其中一种合金的晶胞如图甲所示,晶胞参数 $\alpha=\beta=\gamma = 90^{\circ}$,按图甲中阴影面进行投影得到图乙。
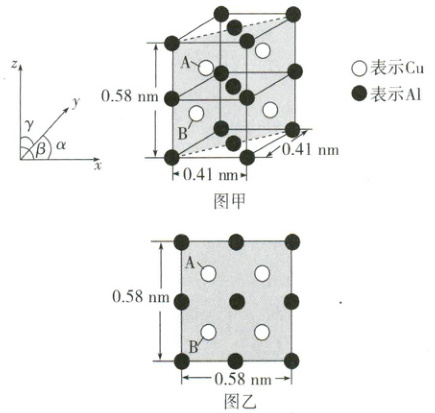
①已知晶胞中 A 点的原子坐标为 $(\frac{1}{2},0,\frac{3}{4})$,则 B 点的原子坐标为
②该晶体的化学式为
LaNi₅
。
(2) 金属铬的晶胞结构如右图所示,已知晶体密度为 7.2 g/cm³,晶体中铬原子的半径为
$\frac{\sqrt{3}}{4}×\sqrt[3]{\frac{52×2}{7.2N_{A}}}$
cm(阿伏加德罗常数的值为 $N_{A}$,不必化简列出表达式即可)。
(3) 金属铜与铝可形成多种组成不同的合金,其中一种合金的晶胞如图甲所示,晶胞参数 $\alpha=\beta=\gamma = 90^{\circ}$,按图甲中阴影面进行投影得到图乙。

①已知晶胞中 A 点的原子坐标为 $(\frac{1}{2},0,\frac{3}{4})$,则 B 点的原子坐标为
(0,$\frac{1}{2}$,$\frac{1}{4}$)
。②该晶体的化学式为
Al₂Cu(或CuAl₂)
,密度约为 4.0
g·cm⁻³(结果保留两位有效数字)。
答案:
(1)$LaNi_{5}$
(2)$\frac{\sqrt{3}}{4}×\sqrt[3]{\frac{52×2}{7.2N_{A}}}$
(3)①(0,$\frac{1}{2}$,$\frac{1}{4}$) ②$Al_{2}Cu$(或$CuAl_{2}$) 4.0
(1)$LaNi_{5}$
(2)$\frac{\sqrt{3}}{4}×\sqrt[3]{\frac{52×2}{7.2N_{A}}}$
(3)①(0,$\frac{1}{2}$,$\frac{1}{4}$) ②$Al_{2}Cu$(或$CuAl_{2}$) 4.0
6. (1) 下图为铜的某种氯化物晶胞示意图。

①该物质的化学式是 $\underline{\quad\quad}$
②原子坐标参数可表示晶胞内部各原子的相对位置,图中各原子坐标参数分别为 $A(0,0,0)$;$B(0,1,1)$;$C(1,1,0)$;$D$ 原子的坐标参数为 $\underline{\quad\quad}$
③晶胞中 $C$、$D$ 两原子核间距为 $298\ pm$,阿伏加德罗常数的值为 $N_{A}$,该晶体的密度为 $\underline{\quad\quad}\ g·cm^{-3}$(列出计算式即可)
(2) 一种四方结构的超导化合物的晶胞如图 1 所示。晶胞中 $Sm$ 和 $As$ 原子的投影位置如图 2 所示。
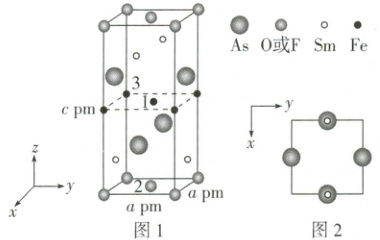
图中 $F^{-}$ 和 $O^{2-}$ 共同占据晶胞的上下底面位置,若两者的比例依次用 $x$ 和 $1 - x$ 代表,则该化合物的化学式表示为 $\underline{\quad\quad}$

①该物质的化学式是 $\underline{\quad\quad}$
CuCl
。②原子坐标参数可表示晶胞内部各原子的相对位置,图中各原子坐标参数分别为 $A(0,0,0)$;$B(0,1,1)$;$C(1,1,0)$;$D$ 原子的坐标参数为 $\underline{\quad\quad}$
($\frac{3}{4}$,$\frac{3}{4}$,$\frac{1}{4}$)
。③晶胞中 $C$、$D$ 两原子核间距为 $298\ pm$,阿伏加德罗常数的值为 $N_{A}$,该晶体的密度为 $\underline{\quad\quad}\ g·cm^{-3}$(列出计算式即可)
$\frac{4×99.5}{N_{A}×(\frac{4×298×10^{-10}}{\sqrt{3}})^{3}}$
。(2) 一种四方结构的超导化合物的晶胞如图 1 所示。晶胞中 $Sm$ 和 $As$ 原子的投影位置如图 2 所示。

图中 $F^{-}$ 和 $O^{2-}$ 共同占据晶胞的上下底面位置,若两者的比例依次用 $x$ 和 $1 - x$ 代表,则该化合物的化学式表示为 $\underline{\quad\quad}$
$SmFeAsO_{1 - x}F_{x}$
;通过测定密度 $\rho$ 和晶胞参数,可以计算该物质的 $x$ 值,完成它们的关系表达式:$\rho=\underline{\quad\quad}\ g·cm^{-3}$$\frac{2×(297 + 3x)}{a^{2}cN_{A}×10^{-30}}$
。以晶胞参数为单位长度建立的坐标系可以表示晶胞中各原子的相对位置,称作原子分数坐标。例如,图 1 中原子 1 的分数坐标为 $(\frac{1}{2},\frac{1}{2},\frac{1}{2})$,则原子 2 和 3 的分数坐标分别为 $\underline{\quad\quad}$($\frac{1}{2}$,$\frac{1}{2}$,0)
、$\underline{\quad\quad}$(0,0,$\frac{1}{2}$)
。
答案:
(1)①CuCl ②($\frac{3}{4}$,$\frac{3}{4}$,$\frac{1}{4}$) ③$\frac{4×99.5}{N_{A}×(\frac{4×298×10^{-10}}{\sqrt{3}})^{3}}$
(2)$SmFeAsO_{1 - x}F_{x}$ $\frac{2×(297 + 3x)}{a^{2}cN_{A}×10^{-30}}$ ($\frac{1}{2}$,$\frac{1}{2}$,0) (0,0,$\frac{1}{2}$)
(1)①CuCl ②($\frac{3}{4}$,$\frac{3}{4}$,$\frac{1}{4}$) ③$\frac{4×99.5}{N_{A}×(\frac{4×298×10^{-10}}{\sqrt{3}})^{3}}$
(2)$SmFeAsO_{1 - x}F_{x}$ $\frac{2×(297 + 3x)}{a^{2}cN_{A}×10^{-30}}$ ($\frac{1}{2}$,$\frac{1}{2}$,0) (0,0,$\frac{1}{2}$)
查看更多完整答案,请扫码查看


