《2025年核心素养学练评六年级数学上册人教版》

3. 在长 6 分米,宽 4 分米的长方形花布上剪下一个最大的圆布片,剩下的部分与圆布相比,谁大? 大的比小的多多少平方分米的布? (4 分)

答案： 圆布大，3.14×(4÷2)²=12.56(平方分米)，12.56−(6×4−12.56)=1.12(平方分米)

4. 如图,街心公园有两块半圆形的草坪,中间夹有一条小路,草坪的周长之和是 257 m,这两块草坪的总面积是多少? (5 分)

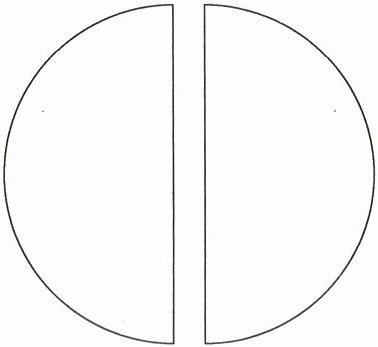
答案： 直径:257÷5.14=50(米),半径:50÷2=25(米),面积:25²×3.14=1962.5(平方米)

5. 学习了圆环的面积,芳芳想:“圆环的大小是由谁来决定的呢?”于是她画了 3 个圆环示意图,下面是她的研究过程。(8 分)

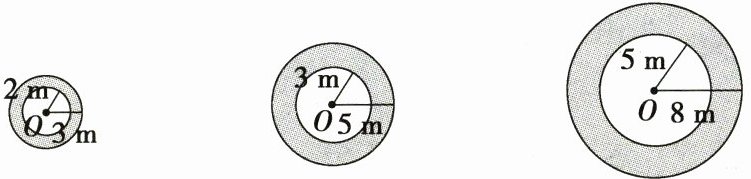
(1) 请分别用含 $\pi$ 的式子表示三个圆环的面积:(5π)m^2、(16π)m^2、(39π)m^2。(3 分)
(2) 通过以上研究,芳芳发现:“三个圆环的环宽分别是 1 m、2 m、3 m,所以环宽越大圆环面积越大。”你同意她的发现吗? 请说明你的理由。(5 分)
不同意。以图中圆环为例，第二个圆环环宽是5−3=2(m)，面积是50.24m²，如果一个圆环的大圆半径是10m，小圆半径是9m，则环宽是10−9=1(m),1m＜2m,圆环面积是3.14×(10²−9²)=59.66(m²),59.66＞50.24。所以并不是环宽越大圆环面积就越大。(理由合理即可)

答案：
(1)5π　16π　39π　
(2)不同意。以图中圆环为例，第二个圆环环宽是5−3=2(m)，面积是50.24m²，如果一个圆环的大圆半径是10m，小圆半径是9m，则环宽是10−9=1(m),1m＜2m,圆环面积是3.14×(10²−9²)=59.66(m²),59.66＞50.24。所以并不是环宽越大圆环面积就越大。(理由合理即可)