第4页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
(1) 在①$\frac {3}{7}+\frac {3}{7}+... +\frac {3}{7}$(10 个$\frac {3}{7}$相加)、②$\frac {10}{7}+\frac {10}{7}+\frac {10}{7}$,③$\frac {10}{7}×3$中,这三个算式的计算结果相比,(
A.算式①的大
B.算式②的大
C.算式③的大
D.一样大
D
)A.算式①的大
B.算式②的大
C.算式③的大
D.一样大
答案:
(1)D 【点拨】①10个$\frac{3}{7}$的和是$10×\frac{3}{7}=\frac{30}{7}$,②$\frac{10}{7}+\frac{10}{7}+\frac{10}{7}=\frac{10}{7}×3=\frac{30}{7}$,③$\frac{10}{7}×3=\frac{30}{7}$,因此这三个算式的结果一样大。
(1)D 【点拨】①10个$\frac{3}{7}$的和是$10×\frac{3}{7}=\frac{30}{7}$,②$\frac{10}{7}+\frac{10}{7}+\frac{10}{7}=\frac{10}{7}×3=\frac{30}{7}$,③$\frac{10}{7}×3=\frac{30}{7}$,因此这三个算式的结果一样大。
(2) 新思维 逆向思维 根据$\frac {4}{15}×\overset{3}{\underset{5}{◯}}$约分的过程,可以知道$◯ =$(
A.3
B.15
C.12
D.9
9
)。A.3
B.15
C.12
D.9
答案:
(2)D 【点拨】由题可知,原分母为15,约分后为5,所以在约分的过程中分母和整数同时除以了3。$◯÷3=3$,所以$◯=9$。
(2)D 【点拨】由题可知,原分母为15,约分后为5,所以在约分的过程中分母和整数同时除以了3。$◯÷3=3$,所以$◯=9$。
2. 计算下列各题。
$\frac {2}{15}×7=$
$3×\frac {3}{20}=$
$\frac {5}{8}×6=$
$12×\frac {4}{9}=$
$\frac {7}{15}×0=$
$\frac {13}{24}×8=$
$\frac {2}{15}×7=$
$\frac{14}{15}$
$3×\frac {3}{20}=$
$\frac{9}{20}$
$\frac {5}{8}×6=$
$\frac{15}{4}$
$12×\frac {4}{9}=$
$\frac{16}{3}$
$\frac {7}{15}×0=$
0
$\frac {13}{24}×8=$
$\frac{13}{3}$
答案:
$\frac{14}{15}$ $\frac{9}{20}$ $\frac{15}{4}$ $\frac{16}{3}$ 0 $\frac{13}{3}$ 【点拨】分数乘整数,用分子乘整数的积作分子,分母不变;整数与分母能约分的,先约分再计算。
3. 看图列式计算。
]
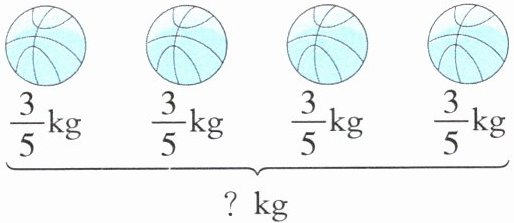
]

答案:
$\frac{3}{5} × 4 = \frac{12}{5}(kg)$
4. 据了解,坚持每天行走 6000 步以上,可以有效促进人体健康。一天,荣老师行走了 12000 步,德老师行走的步数是荣老师的$\frac {8}{15}$,德老师这一天的步数够 6000 步吗?
答案:
$12000×\frac{8}{15}=6400$(步)$6400>6000$答:德老师这一天的步数够6000步。
(1) 在$◯$里填上“>”“<”或“=”。
$\frac {5}{7}×\frac {3}{4}$
$\frac {7}{8}×\frac {6}{5}$
$\frac {3}{10}$
$\frac {11}{12}×\frac {7}{6}$
$\frac {5}{7}×\frac {3}{4}$
<
$\frac {5}{7}$$\frac {7}{8}×\frac {6}{5}$
>
$\frac {7}{8}$$\frac {3}{10}$
=
$\frac {1}{4}×\frac {6}{5}$$\frac {11}{12}×\frac {7}{6}$
<
$\frac {7}{6}$
答案:
(1)$<$ $>$ $=$ $<$ 【点拨】可根据算式的特点,利用积与因数的大小关系判断。一个不为0的数乘小于1的数,得数小于原来的数;一个不为0的数乘大于1的数,得数大于原来的数。
(1)$<$ $>$ $=$ $<$ 【点拨】可根据算式的特点,利用积与因数的大小关系判断。一个不为0的数乘小于1的数,得数小于原来的数;一个不为0的数乘大于1的数,得数大于原来的数。
(2) 一个修路队平均每时修路$\frac {4}{9}km$,$\frac {5}{6}$时修路(
$\frac{10}{27}$
)km,30 分修路($\frac{2}{9}$
)km。
答案:
(2)$\frac{10}{27}$ $\frac{2}{9}$
(2)$\frac{10}{27}$ $\frac{2}{9}$
(1)【新考法 数形结合法 重庆市期中】 数学家华罗庚说过:“数缺形时少直观,形少数时难入微。”下面能正确表示算式$\frac {1}{4}×\frac {1}{4}$的图有(
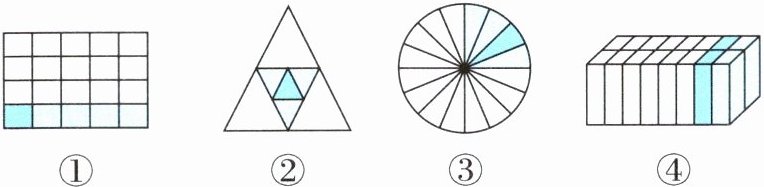
A.①②
B.①③
C.③④
D.②③
D
)。
A.①②
B.①③
C.③④
D.②③
答案:
(1)D
(1)D
(2) 下列算式(
A.$\frac {3}{8}×\frac {1}{3}$
B.$\frac {8}{9}×\frac {3}{2}$
C.$\frac {1}{3}×\frac {3}{4}$
D.$\frac {8}{9}×\frac {3}{4}$
D
)的积在$\frac {1}{3}和\frac {8}{9}$之间。A.$\frac {3}{8}×\frac {1}{3}$
B.$\frac {8}{9}×\frac {3}{2}$
C.$\frac {1}{3}×\frac {3}{4}$
D.$\frac {8}{9}×\frac {3}{4}$
答案:
(2)D【点拨】A、C的积小于$\frac{1}{3}$,B的积大于$\frac{8}{9}$。
(2)D【点拨】A、C的积小于$\frac{1}{3}$,B的积大于$\frac{8}{9}$。
7. 计算下列各题。
$\frac {7}{11}×\frac {4}{9}=$
$\frac {9}{10}×\frac {5}{12}=$
$\frac {17}{42}×\frac {35}{51}×\frac {3}{2}=$
$\frac {15}{26}×\frac {13}{25}=$
$\frac {5}{13}×16×\frac {39}{25}=$
$\frac {7}{11}×\frac {4}{9}=$
$\frac{28}{99}$
$\frac {9}{10}×\frac {5}{12}=$
$\frac{3}{8}$
$\frac {17}{42}×\frac {35}{51}×\frac {3}{2}=$
$\frac{5}{12}$
$\frac {15}{26}×\frac {13}{25}=$
$\frac{3}{10}$
$\frac {5}{13}×16×\frac {39}{25}=$
$\frac{48}{5}$
答案:
$\frac{28}{99}$ $\frac{3}{8}$ $\frac{5}{12}$ $\frac{3}{10}$ $\frac{48}{5}$
8. 母题 教材$P6习题T14$ 蜀绣是中国四大名绣之一。一家蜀绣工坊制作了一批长方体收纳盒,用来存放细小针线等工具。一个收纳盒的长是$\frac {6}{7}$分米,宽和高都是$\frac {1}{4}$分米,它的体积是多少立方分米?
答案:
$\frac{6}{7}×\frac{1}{4}×\frac{1}{4}=\frac{3}{56}$(立方分米)答:它的体积是$\frac{3}{56}$立方分米。【点拨】长方体的体积=长×宽×高。
查看更多完整答案,请扫码查看


