《2025年预学与导学五年级数学上册人教版》

1. 根据等式或数的规律,求出下面这些符号或字母所表示的数。
(1)如果 $ x + 3 = 15 $,那么 $ x = $ (12)。
(2)如果 $ \triangle ÷ □ = 22 $,$ □ = 6 $,那么 $ \triangle = $(132)。

答案：
(1)12；
(2)132

2. (1)如果用 a,b,c 分别表示 3 个加数,那么加法结合律可以用字母表示为：(a+b)+c=a+(b+c)。
(2)如果用 a,b,c 分别表示 3 个不同的数,那么乘法分配律和乘法结合律可以分别用字母表示为(a+b)×c=a×c+b×c,(a×b)×c=a×(b×c)。

答案：
(1) (a+b)+c=a+(b+c)
(2) (a+b)×c=a×c+b×c ；(a×b)×c=a×(b×c)

3. 省略乘号,写出下面各式。
$ a × 5 = $5a $ 1 × b = $b $ b × m = $bm $ a × a = $a²

答案： 答题卡：
3.
$a × 5 = 5a$
$1 × b = b$
$b × m = bm$
$a × a = a^{2}$

4. (1)如果一种动物的奔跑速度是 70 千米/时,那么它 2 小时奔跑(140)km,3.5 小时奔跑(245)km,t 小时奔跑(70t)km。
(2)哈雷彗星每 76 年出现一次,在公元 s 年出现后,下一次出现是在公元(s + 76)年。

答案：
(1) 140；245；70t
(2) s + 76

5. 王叔叔每小时加工 x 个零件,3 小时加工 3x 个零件。你能再举一个生活中的事例来解释 3x 吗？

答案： 答：举例：若每支铅笔的价格是 x 元，那么购买 3 支铅笔的总价格就是 3x 元。

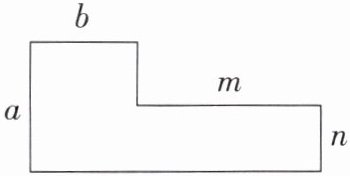
请你用含有字母的式子表示下图的周长和面积。

答案： 周长：
$C = 2(a + b + m)$
面积：
$S = ab + mn$