《2025年物理学堂八年级上册教科版》

例3 分辨下面的描述各指声音的哪一种特性？
(1)“上下楼梯,轻声慢步”是指声音的______。
(2)“窃窃私语”是指声音的______。
(3)空中响起了“沉闷的雷声”是指声音的______。
(4)“女高音,男低音”是指声音的______。

答案：
(1)响度
(2)响度
(3)音调
(4)音调

例4 根据波形图,回答下列问题。
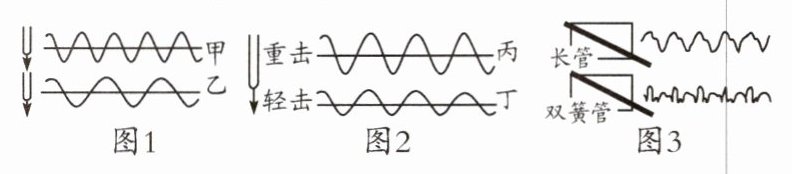
(1)有两个不同的音叉,示波器分别显示出其声波的图形,如图1。甲、乙比较,______音调低。
(2)图2是同一音叉,示波器显示出重击和轻击它时声波的图形。丙、丁比较,______响度小。
(3)图3中能区分两乐器的演奏声是因为它们发出声音的______不同。

答案： 【解析】：
本题主要考查声音的特性，包括音调、响度和音色，以及如何通过波形图来判断这些特性。
（1）对于音调，知道它是由发声体振动的频率决定的，频率越低，音调越低。观察图1中甲、乙两个波形图，可以看到在相同的时间内，甲音叉的振动次数较少，即甲音叉的振动频率较低，因此甲音叉的音调较低。
综上所述，本题答案为：甲。
（2）对于响度，它是由发声体振动的振幅决定的，振幅越小，响度越小。观察图2中丙、丁两个波形图，可以看到丙音叉的波形振幅较大，表示重击时响度大；而丁音叉的波形振幅较小，表示轻击时响度小。
综上所述，本题答案为：丁。
（3）对于音色，它是由于发声体的材料和结构不同而产生的，不同发声体的音色一般不同。观察图3中的两个波形图，虽然它们的音调和响度可能相同，但由于发声体的材料和结构不同，导致它们的波形形状不同，即音色不同。因此，可以通过音色来区分两乐器的演奏声。
综上所述，本题答案为：音色。
【答案】：
（1）甲；（2）丁；（3）音色。

例5 下列四个选项中的做法,能在传播过程中有效地减弱噪声的是( )

A.市区道路行车禁鸣汽车喇叭
B.机器旁人员佩戴防噪声耳罩
C.在路口处安装噪声监测装置
D.在高架路的两旁修建隔声板

答案： 【解析】：
本题主要考查噪声的控制方法，特别是在传播过程中如何有效地减弱噪声。
A选项，市区道路行车禁鸣汽车喇叭，这是在声源处减弱噪声，即防止噪声的产生，不符合题目要求的在传播过程中减弱噪声，所以A错误。
B选项，机器旁人员佩戴防噪声耳罩，这是人耳处减弱噪声，即防止噪声进入人耳，也不符合题目要求的在传播过程中减弱噪声，所以B错误。
C选项，在路口处安装噪声监测装置，这只是用来监测噪声的强弱，并不能有效地减弱噪声，所以C错误。
D选项，在高架路的两旁修建隔声板，这是在噪声的传播过程中设置障碍，使噪声在传播过程中受到阻挡，从而有效地减弱噪声，所以D正确。
【答案】：
D

例6 司机倒车时因看不到车后的情况很容易撞到障碍物。倒车防撞雷达可以测量出与障碍物之间的距离,并在车与障碍物之间距离过小时发出警报提醒司机。某次倒车防撞雷达向障碍物发出信号后,经过0.02 s接收装置收到返回的信号。($v_{声}= 340\ m/s$)
(1)倒车防撞雷达利用______来测量距离。
(2)上述过程中车尾与障碍物之间的距离大约是多少？
(3)如果倒车速度为0.1 m/s,要使车停止时车尾与障碍物之间的距离为0.4 m,则倒车时间为多长？

答案：
(1)超声波
(2)解：由题意可知，信号从发出到接收经过的时间$t = 0.02\space s$，声音在空气中的传播速度$v_{声}=340\space m/s$。
信号从车尾到障碍物再返回车尾，经过的路程是车尾与障碍物之间距离$s$的$2$倍，即$2s=v_{声}t$。
则$s=\frac{v_{声}t}{2}=\frac{340\space m/s×0.02\space s}{2}=3.4\space m$
(3)解：已知车尾与障碍物之间的初始距离$s = 3.4\space m$，车停止时车尾与障碍物之间的距离$s'=0.4\space m$，倒车速度$v = 0.1\space m/s$。
倒车的距离$s_{倒车}=s - s'=3.4\space m - 0.4\space m=3\space m$。
根据$v=\frac{s}{t}$，可得倒车时间$t=\frac{s_{倒车}}{v}=\frac{3\space m}{0.1\space m/s}=30\space s$

例7 地震发生时,震源同时产生并向各个方向发出纵波和横波,科学家利用地震波中纵波和横波传播速度不同的特点,可以监测到震源的位置。2024年10月16日,台湾花莲海域发生4.4级地震,台湾地震观测点监测到这两种波先后到达的时间间隔为6 s。已知纵波速度$v_{纵}= 5\ km/s$,横波速度$v_{横}= 3\ km/s$。求：
(1)震源到台湾地震观测点的距离为多少千米？
(2)该震源到连江地震观测点的直线距离有330 km,两种波到达的时间间隔为多少秒？

答案： 【解析】：
本题主要考查速度公式$v=\frac{s}{t}$（$v$表示速度，$s$表示路程，$t$表示时间）的应用，需要根据纵波和横波的速度以及它们到达观测点的时间间隔来求解震源到观测点的距离，或者根据距离和速度求时间间隔。
(1)设震源到台湾地震观测点的距离为$s$，纵波到达观测点的时间为$t_{纵}$，横波到达观测点的时间为$t_{横}$。
根据速度公式$v = \frac{s}{t}$，可得$t=\frac{s}{v}$，那么$t_{纵}=\frac{s}{v_{纵}}$，$t_{横}=\frac{s}{v_{横}}$。
已知两种波先后到达的时间间隔为$6s$，即$t_{横}-t_{纵}=6s$，将$t_{纵}=\frac{s}{v_{纵}}$，$t_{横}=\frac{s}{v_{横}}$代入可得：
$\frac{s}{v_{横}}-\frac{s}{v_{纵}} = 6s$
把$v_{纵}= 5km/s$，$v_{横}= 3km/s$代入上式得：
$\frac{s}{3}-\frac{s}{5}=6$
通分可得：$\frac{5s}{15}-\frac{3s}{15}=6$
即$\frac{2s}{15}=6$
两边同时乘以$\frac{15}{2}$，解得$s = 45km$。
(2)已知该震源到连江地震观测点的直线距离$s' = 330km$，根据$t=\frac{s}{v}$，可得纵波到达连江地震观测点的时间$t_{纵}'=\frac{s'}{v_{纵}}=\frac{330}{5}=66s$，横波到达连江地震观测点的时间$t_{横}'=\frac{s'}{v_{横}}=\frac{330}{3}=110s$。
则两种波到达的时间间隔$\Delta t=t_{横}'-t_{纵}'=110 - 66 = 44s$。
【答案】：
(1)震源到台湾地震观测点的距离为$45km$。
(2)两种波到达的时间间隔为$44s$。