2025年暑假生活五年级数学西师大版重庆出版社
注:目前有些书本章节名称可能整理的还不是很完善,但都是按照顺序排列的,请同学们按照顺序仔细查找。练习册 2025年暑假生活五年级数学西师大版重庆出版社 答案主要是用来给同学们做完题方便对答案用的,请勿直接抄袭。
1. 等式两边同时乘或除以同一个数,等式仍然成立。(
×
)
答案:
×
如果$\frac {x}{12}$是真分数,$\frac {x+1}{12}$是假分数,那么自然数$x=12$。(
×
)
答案:
×
3. $5x+4$不是方程。(
√
)
答案:
√
4. 如果$3x=5$,那么$\frac {1}{3}+x=2$。(
√
)
答案:
√
5. 方程$7x=0$没有解。(
×
)
答案:
×
1. 已知$6x+3=37x$,请在下面的〇里填上“>”“<”或“=”。
$6x+3$〇$37x-2$ 应填
$(6x+3)-5$〇$37x$ 应填
$6x+3-9$〇$37x-9$ 应填
$6x+3$〇$37x-2$ 应填
>
$(6x+3)-5$〇$37x$ 应填
<
$6x+3-9$〇$37x-9$ 应填
=
答案:
>,<,=
2. 在括号里填上合适的质数。
$40=(
$40=(
3
)+(37
)=(11
)+(29
)=(17
)+(23
)=(23
)+(17
)$
答案:
3、37;11、29;17、23;23、17(答案不唯一,只要满足两个数都是质数且和为 40 即可)
$(
3
)×(4
)-(5
)=(8
)÷(2
)+(6
)-(7
)=(7
)$
答案:
$3$、$4$、$5$、$8$、$2$、$6$、$7$、$7$
1. 脱式计算,能简算的要简算。
$\frac {11}{12}+\frac {5}{8}+\frac {3}{8}+\frac {1}{12}$ $\frac {11}{12}-(\frac {1}{6}+\frac {1}{8})$ $\frac {1}{2}+\frac {1}{4}+\frac {1}{8}+\frac {1}{16}+\frac {1}{32}$
$\frac {11}{12}+\frac {5}{8}+\frac {3}{8}+\frac {1}{12}$ $\frac {11}{12}-(\frac {1}{6}+\frac {1}{8})$ $\frac {1}{2}+\frac {1}{4}+\frac {1}{8}+\frac {1}{16}+\frac {1}{32}$
答案:
【解析】:
- 对于$\frac {11}{12}+\frac {5}{8}+\frac {3}{8}+\frac {1}{12}$,根据加法交换律$a + b=b + a$和加法结合律$(a + b)+c=a+(b + c)$进行简便计算。将$\frac{11}{12}$与$\frac{1}{12}$结合,$\frac{5}{8}$与$\frac{3}{8}$结合,可得$(\frac{11}{12}+\frac{1}{12})+(\frac{5}{8}+\frac{3}{8})$,先分别计算括号内的值,$\frac{11}{12}+\frac{1}{12} = 1$,$\frac{5}{8}+\frac{3}{8}=1$,再将结果相加$1 + 1=2$。
- 对于$\frac {11}{12}-(\frac {1}{6}+\frac {1}{8})$,先计算括号内的加法,需要先通分,$6$和$8$的最小公倍数是$24$,则$\frac{1}{6}=\frac{1×4}{6×4}=\frac{4}{24}$,$\frac{1}{8}=\frac{1×3}{8×3}=\frac{3}{24}$,那么$\frac{1}{6}+\frac{1}{8}=\frac{4}{24}+\frac{3}{24}=\frac{7}{24}$;再计算括号外的减法,$\frac{11}{12}-\frac{7}{24}$,$\frac{11}{12}=\frac{11×2}{12×2}=\frac{22}{24}$,所以$\frac{11}{12}-\frac{7}{24}=\frac{22}{24}-\frac{7}{24}=\frac{15}{24}=\frac{5}{8}$。
- 对于$\frac {1}{2}+\frac {1}{4}+\frac {1}{8}+\frac {1}{16}+\frac {1}{32}$,可采用借一还一的方法,先加上$\frac{1}{32}$再减去$\frac{1}{32}$,即$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32}-\frac{1}{32}$。$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{2}{32}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{16}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{2}{16}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}+\frac{1}{4}+\frac{2}{8}=\frac{1}{2}+\frac{1}{4}+\frac{1}{4}=\frac{1}{2}+\frac{2}{4}=\frac{1}{2}+\frac{1}{2}=1$,所以$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=1 - \frac{1}{32}=\frac{31}{32}$。
【答案】:$2$;$\frac{5}{8}$;$\frac{31}{32}$
- 对于$\frac {11}{12}+\frac {5}{8}+\frac {3}{8}+\frac {1}{12}$,根据加法交换律$a + b=b + a$和加法结合律$(a + b)+c=a+(b + c)$进行简便计算。将$\frac{11}{12}$与$\frac{1}{12}$结合,$\frac{5}{8}$与$\frac{3}{8}$结合,可得$(\frac{11}{12}+\frac{1}{12})+(\frac{5}{8}+\frac{3}{8})$,先分别计算括号内的值,$\frac{11}{12}+\frac{1}{12} = 1$,$\frac{5}{8}+\frac{3}{8}=1$,再将结果相加$1 + 1=2$。
- 对于$\frac {11}{12}-(\frac {1}{6}+\frac {1}{8})$,先计算括号内的加法,需要先通分,$6$和$8$的最小公倍数是$24$,则$\frac{1}{6}=\frac{1×4}{6×4}=\frac{4}{24}$,$\frac{1}{8}=\frac{1×3}{8×3}=\frac{3}{24}$,那么$\frac{1}{6}+\frac{1}{8}=\frac{4}{24}+\frac{3}{24}=\frac{7}{24}$;再计算括号外的减法,$\frac{11}{12}-\frac{7}{24}$,$\frac{11}{12}=\frac{11×2}{12×2}=\frac{22}{24}$,所以$\frac{11}{12}-\frac{7}{24}=\frac{22}{24}-\frac{7}{24}=\frac{15}{24}=\frac{5}{8}$。
- 对于$\frac {1}{2}+\frac {1}{4}+\frac {1}{8}+\frac {1}{16}+\frac {1}{32}$,可采用借一还一的方法,先加上$\frac{1}{32}$再减去$\frac{1}{32}$,即$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32}-\frac{1}{32}$。$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}+\frac{1}{32}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{2}{32}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{16}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{2}{16}=\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{8}=\frac{1}{2}+\frac{1}{4}+\frac{2}{8}=\frac{1}{2}+\frac{1}{4}+\frac{1}{4}=\frac{1}{2}+\frac{2}{4}=\frac{1}{2}+\frac{1}{2}=1$,所以$\frac{1}{2}+\frac{1}{4}+\frac{1}{8}+\frac{1}{16}+\frac{1}{32}=1 - \frac{1}{32}=\frac{31}{32}$。
【答案】:$2$;$\frac{5}{8}$;$\frac{31}{32}$
智慧考验




答案:
如图所示: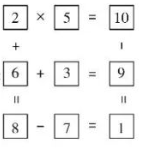
如图所示:

查看更多完整答案,请扫码查看


