1. 角的常用画法: (1) 度量法(使用量角器或三角尺); (2) 尺规作图(使用
无刻度的直尺和圆规
).
答案:
无刻度的直尺和圆规
2. 如果从角的顶点出发的一条射线把这个角分成两个
相等
的角, 那么这条射线叫作这个角的平分线.
答案:
相等
1. 下列角度: ① $ 15 ^ { \circ } $; ② $ 65 ^ { \circ } $; ③ $ 75 ^ { \circ } $; ④ $ 115 ^ { \circ } $; ⑤ $ 135 ^ { \circ } $. 可以用一副三角尺画出来的是 (
A.②④⑤
B.①②④
C.①③⑤
D.①③④
C
)A.②④⑤
B.①②④
C.①③⑤
D.①③④
答案:
C
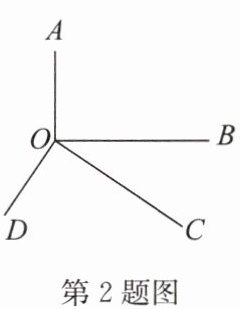
2. 如图, $ \angle AOB = \angle COD = 90 ^ { \circ } $, $ \angle AOD = 146 ^ { \circ } $, 则 $ \angle BOC $ 的度数为 (
A.$ 43 ^ { \circ } $
B.$ 34 ^ { \circ } $
C.$ 56 ^ { \circ } $
D.$ 50 ^ { \circ } $
B
) 
A.$ 43 ^ { \circ } $
B.$ 34 ^ { \circ } $
C.$ 56 ^ { \circ } $
D.$ 50 ^ { \circ } $
答案:
B
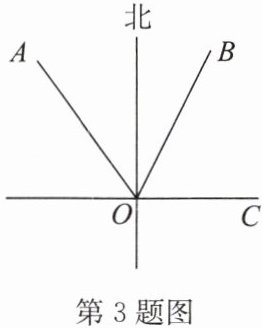
3. 如图, 射线 $ OA $ 表示北偏西 $ 36 ^ { \circ } $ 方向, $ OB $ 平分 $ \angle AOC $, 则 $ \angle BOC = $
63
$ ^ { \circ } $.
答案:
63
4. 如图, $ O $ 为直线 $ AB $ 上一点, $ OC $ 平分 $ \angle AOD $, $ \angle BOD = 30 ^ { \circ } $, 求 $ \angle AOC $ 的度数.


答案:
解:因为∠BOD=30°,
所以∠AOD=180°-∠BOD=180°-30°=150°.
因为 OC 平分∠AOD,
所以∠AOC=$\frac{1}{2}$∠AOD=75°.
所以∠AOD=180°-∠BOD=180°-30°=150°.
因为 OC 平分∠AOD,
所以∠AOC=$\frac{1}{2}$∠AOD=75°.
5. 如图, $ \angle AOB $ 是平角, $ OM $, $ ON $ 分别是 $ \angle AOC $, $ \angle BOD $ 的平分线.
(1) 若 $ \angle AOC = 40 ^ { \circ } $, $ \angle BOD = 60 ^ { \circ } $, 求 $ \angle MON $ 的度数;
(2) 若只给条件“$ \angle COD = 80 ^ { \circ } $”,你能求出 $ \angle MON $ 的度数吗? 如果能, 请给出求解过程; 如果不能, 请说明理由.

(1) 若 $ \angle AOC = 40 ^ { \circ } $, $ \angle BOD = 60 ^ { \circ } $, 求 $ \angle MON $ 的度数;
(2) 若只给条件“$ \angle COD = 80 ^ { \circ } $”,你能求出 $ \angle MON $ 的度数吗? 如果能, 请给出求解过程; 如果不能, 请说明理由.

答案:
1. (1)
因为$OM$平分$\angle AOC$,$\angle AOC = 40^{\circ}$,根据角平分线定义:
则$\angle MOC=\frac{1}{2}\angle AOC$,所以$\angle MOC=\frac{1}{2}×40^{\circ}=20^{\circ}$。
因为$ON$平分$\angle BOD$,$\angle BOD = 60^{\circ}$,根据角平分线定义:
则$\angle DON=\frac{1}{2}\angle BOD$,所以$\angle DON=\frac{1}{2}×60^{\circ}=30^{\circ}$。
又因为$\angle AOB$是平角,$\angle AOB = 180^{\circ}$,$\angle AOB=\angle AOC+\angle COD+\angle BOD$,所以$\angle COD=\angle AOB - \angle AOC-\angle BOD$,$\angle COD = 180^{\circ}-40^{\circ}-60^{\circ}=80^{\circ}$。
那么$\angle MON=\angle MOC+\angle COD+\angle DON$。
把$\angle MOC = 20^{\circ}$,$\angle COD = 80^{\circ}$,$\angle DON = 30^{\circ}$代入可得:$\angle MON=20^{\circ}+80^{\circ}+30^{\circ}=130^{\circ}$。
2. (2)
能求出$\angle MON$的度数。
解:因为$OM$平分$\angle AOC$,所以$\angle MOC=\frac{1}{2}\angle AOC$;因为$ON$平分$\angle BOD$,所以$\angle DON=\frac{1}{2}\angle BOD$。
又因为$\angle AOB = 180^{\circ}$,$\angle AOB=\angle AOC+\angle COD+\angle BOD$,所以$\angle AOC+\angle BOD=\angle AOB - \angle COD$。
已知$\angle COD = 80^{\circ}$,则$\angle AOC+\angle BOD=180^{\circ}-80^{\circ}=100^{\circ}$。
而$\angle MON=\angle MOC+\angle COD+\angle DON$,$\angle MOC+\angle DON=\frac{1}{2}(\angle AOC+\angle BOD)$。
把$\angle AOC+\angle BOD = 100^{\circ}$代入$\angle MOC+\angle DON=\frac{1}{2}(\angle AOC+\angle BOD)$得$\angle MOC+\angle DON=\frac{1}{2}×100^{\circ}=50^{\circ}$。
又因为$\angle COD = 80^{\circ}$,所以$\angle MON=\angle MOC+\angle DON+\angle COD$。
把$\angle MOC+\angle DON = 50^{\circ}$,$\angle COD = 80^{\circ}$代入可得$\angle MON=50^{\circ}+80^{\circ}=130^{\circ}$。
综上,(1)$\angle MON$的度数为$130^{\circ}$;(2)能,$\angle MON$的度数为$130^{\circ}$。
因为$OM$平分$\angle AOC$,$\angle AOC = 40^{\circ}$,根据角平分线定义:
则$\angle MOC=\frac{1}{2}\angle AOC$,所以$\angle MOC=\frac{1}{2}×40^{\circ}=20^{\circ}$。
因为$ON$平分$\angle BOD$,$\angle BOD = 60^{\circ}$,根据角平分线定义:
则$\angle DON=\frac{1}{2}\angle BOD$,所以$\angle DON=\frac{1}{2}×60^{\circ}=30^{\circ}$。
又因为$\angle AOB$是平角,$\angle AOB = 180^{\circ}$,$\angle AOB=\angle AOC+\angle COD+\angle BOD$,所以$\angle COD=\angle AOB - \angle AOC-\angle BOD$,$\angle COD = 180^{\circ}-40^{\circ}-60^{\circ}=80^{\circ}$。
那么$\angle MON=\angle MOC+\angle COD+\angle DON$。
把$\angle MOC = 20^{\circ}$,$\angle COD = 80^{\circ}$,$\angle DON = 30^{\circ}$代入可得:$\angle MON=20^{\circ}+80^{\circ}+30^{\circ}=130^{\circ}$。
2. (2)
能求出$\angle MON$的度数。
解:因为$OM$平分$\angle AOC$,所以$\angle MOC=\frac{1}{2}\angle AOC$;因为$ON$平分$\angle BOD$,所以$\angle DON=\frac{1}{2}\angle BOD$。
又因为$\angle AOB = 180^{\circ}$,$\angle AOB=\angle AOC+\angle COD+\angle BOD$,所以$\angle AOC+\angle BOD=\angle AOB - \angle COD$。
已知$\angle COD = 80^{\circ}$,则$\angle AOC+\angle BOD=180^{\circ}-80^{\circ}=100^{\circ}$。
而$\angle MON=\angle MOC+\angle COD+\angle DON$,$\angle MOC+\angle DON=\frac{1}{2}(\angle AOC+\angle BOD)$。
把$\angle AOC+\angle BOD = 100^{\circ}$代入$\angle MOC+\angle DON=\frac{1}{2}(\angle AOC+\angle BOD)$得$\angle MOC+\angle DON=\frac{1}{2}×100^{\circ}=50^{\circ}$。
又因为$\angle COD = 80^{\circ}$,所以$\angle MON=\angle MOC+\angle DON+\angle COD$。
把$\angle MOC+\angle DON = 50^{\circ}$,$\angle COD = 80^{\circ}$代入可得$\angle MON=50^{\circ}+80^{\circ}=130^{\circ}$。
综上,(1)$\angle MON$的度数为$130^{\circ}$;(2)能,$\angle MON$的度数为$130^{\circ}$。
查看更多完整答案,请扫码查看


