《2025年中学生世界八年级物理第一学期沪教版54制》

9. 为了测量教室的长度,选用的刻度尺最合理的是 (C)
A.量程为 0~1 m,分度值是 1 mm
B.量程为 0~10 m,分度值为 1 dm
C.量程为 0~10 m,分度值是 1 cm
D.量程为 0~10 m,分度值为 1 mm

答案： 【解析】：
本题主要考查刻度尺的选择原则，即根据测量要求选择适当量程和分度值的刻度尺。对于教室长度的测量，我们需要考虑两个因素：一是刻度尺的量程要能够覆盖教室的长度，二是刻度尺的分度值要能够满足测量精度的要求。
A选项：量程过小，可能无法覆盖教室的全部长度，故A不合理。
B选项：虽然量程足够，但分度值过大，测量精度不够，故B不合理。
C选项：量程足够测量教室的长度，且分度值为1cm，可以提供足够的测量精度，故C合理。
D选项：量程同样足够，但分度值过小，可能导致不必要的测量成本增加，且在实际操作中可能难以达到如此高的精度，故D不是最佳选择。
综合考虑量程和分度值，C选项是最合理的选择。
【答案】：
C

10. 用厚度较厚的木质刻度尺测量某长方体的长时,图 2 中使用刻度尺正确的是 (D)

答案： 解：使用刻度尺测量长度时，应使刻度尺有刻度的一边紧贴被测物体，且与被测边保持平行，零刻度线或某一整刻度线与被测物体的起始端对齐。
A图中刻度尺有刻度的一边未紧贴被测物体；B图中刻度尺未与被测边保持平行；C图中刻度尺有刻度的一边未紧贴被测物体；D图符合刻度尺的正确使用方法。
答案：D

11. 小明用如图 3 所示的方法测量球的直径,他的测量结果是 (D)
A.6.2 cm
B.5.0 cm
C.2.4 cm
D.1.2 cm

答案： 解：由图可知，刻度尺的分度值为1mm。球左侧对应的刻度值为5.00cm，右侧对应的刻度值为6.20cm。球的直径为右侧刻度值减去左侧刻度值，即6.20cm - 5.00cm = 1.20cm，测量结果保留一位小数为1.2cm。
D

12. 完成下列单位换算(要求写出换算过程):
(1) $ 0.05 \, m^2 = $______$0.05 × 10000cm^{2}$$ = $______$500$$ cm^2 $.
(2) $ 80 \, cm^3 = $______$\frac{80}{1000000}m^{3}$$ = $______$8 × 10^{- 5}$$ m^3 $.

答案： 【解析】：
本题主要考查单位换算，需要知道1米等于100厘米，1平方米等于$10000$平方厘米，1立方米等于$1000000$立方厘米，然后进行相应的换算。
(1) 对于$0.05m^{2}$，我们需要将其转换为$cm^{2}$。由于$1m = 100cm$，所以$1m^{2} = (100cm)^{2} = 10000cm^{2}$。因此，$0.05m^{2}$等于$0.05 × 10000cm^{2}$，即$500cm^{2}$。
(2) 对于$80cm^{3}$，我们需要将其转换为$m^{3}$。由于$1m = 100cm$，所以$1m^{3} = (100cm)^{3} = 1000000cm^{3}$。为了从$cm^{3}$转换为$m^{3}$，我们需要除以$1000000$。因此，$80cm^{3}$等于$\frac{80}{1000000} m^{3}$，即$8 × 10^{- 5}m^{3}$。
【答案】：
(1) $0.05m^{2} = 0.05 × 10000cm^{2} = 500cm^{2}$
(2) $80cm^{3} = \frac{80}{1000000}m^{3} = 8 × 10^{- 5}m^{3}$

1. 一般物质都有热胀冷缩的规律. 如果用从低温环境中取出的一把金属刻度尺立即去测量常温下某个物体的长度,这样测出的结果将会比被测物体的真实长度 (A)
A.偏小
B.偏大
C.没有影响
D.以上均有可能

答案： 解：金属刻度尺从低温环境取出后，由于热胀冷缩，刻度尺会因温度升高而膨胀，刻度间距变大。用膨胀后的刻度尺测量常温下物体长度时，读取的刻度值会比物体真实长度小。
结论：测出的结果比真实长度偏小。
答案：A

2. 为了测量一个形状不规则的薄壁玻璃瓶的容积,小明设计了如下方法:
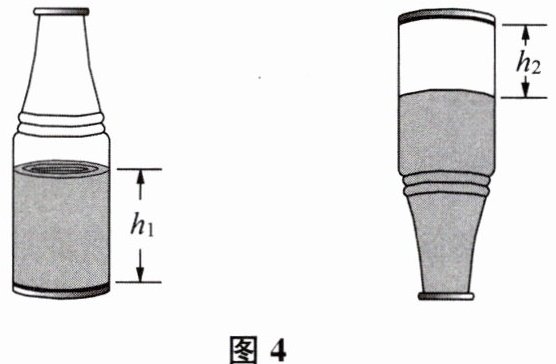
他先用刻度尺测出瓶底直径为 $ d $,在瓶中倒入适量的水,测出瓶中水面距瓶底的距离为 $ h_1 $. 然后再堵住瓶口,将瓶竖直倒置后测出水面距瓶底的距离为 $ h_2 $,如图 4 所示.

(1) 该玻璃瓶圆柱形部分的横截面积是$\frac{\pi d^2}{4}$.
(2) 该瓶的容积是$\frac{\pi d^2}{4}(h_1 + h_2)$. (结果均用已知的符号及常数表示)

答案： 【解析】：
本题可根据圆的面积公式求出玻璃瓶圆柱形部分的横截面积，再通过分析玻璃瓶正放和倒放时水的体积与空的部分的体积关系来求解玻璃瓶的容积。
（1）求玻璃瓶圆柱形部分的横截面积
已知瓶底直径为$d$，根据圆的面积公式$S = \pi r^2$（其中$S$为圆的面积，$r$为圆的半径），可得半径$r=\frac{d}{2}$，则玻璃瓶圆柱形部分的横截面积$S$为：
$S = \pi(\frac{d}{2})^2=\frac{\pi d^2}{4}$
（2）求玻璃瓶的容积
步骤一：求出瓶中水的体积$V_{水}$
当瓶正放时，瓶中水面距瓶底的距离为$h_1$，由（1）已求得圆柱形部分的横截面积为$S = \frac{\pi d^2}{4}$，根据圆柱体积公式$V = Sh$（其中$V$为圆柱体积，$S$为底面积，$h$为高），可得瓶中水的体积$V_{水}=S h_1=\frac{\pi d^2}{4}h_1$。
步骤二：求出瓶中空的部分的体积$V_{空}$
当瓶倒置后，水面距瓶底的距离为$h_2$，此时空的部分可看作是一个高为$h_2$的圆柱体，其底面积同样为$S = \frac{\pi d^2}{4}$，根据圆柱体积公式可得空的部分的体积$V_{空}=S h_2=\frac{\pi d^2}{4}h_2$。
步骤三：求出玻璃瓶的容积$V$
玻璃瓶的容积等于瓶中水的体积与空的部分的体积之和，即$V = V_{水} + V_{空}=\frac{\pi d^2}{4}h_1 + \frac{\pi d^2}{4}h_2=\frac{\pi d^2}{4}(h_1 + h_2)$。
【答案】：
(1)$\frac{\pi d^2}{4}$
(2)$\frac{\pi d^2}{4}(h_1 + h_2)$