《2025年中学生世界八年级物理第一学期沪教版54制》

6. 如图3所示,光线斜射到镜面上,保持入射光线的方向不变,将平面镜绕入射点$O逆时针旋转5^{\circ}$后,则反射光线将朝逆(选填“顺”或“逆”)时针方向旋转,转过的角度是10度.

答案： 【解析】：
本题主要考查光的反射定律的应用。当入射光线方向不变，而平面镜发生旋转时，反射光线的方向也会相应发生变化。
首先，我们需要明确光的反射定律：反射光线、入射光线和法线都处于同一平面内，且反射光线和入射光线的角度相等，这个角度是相对于法线的。
当平面镜绕入射点$O$逆时针旋转$5^{\circ}$后，法线也会相应逆时针旋转$5^{\circ}$。由于入射光线方向不变，所以入射角（即入射光线和法线的夹角）会增加$5^{\circ}$。
根据光的反射定律，反射角（即反射光线和法线的夹角）也会增加$5^{\circ}$。
由于法线逆时针旋转了$5^{\circ}$，反射光线相对于原来的位置就会逆时针旋转。但考虑到反射角增加了$5^{\circ}$，同时入射角也增加了$5^{\circ}$，所以反射光线实际上会朝逆时针方向旋转$2 × 5^{\circ} = 10^{\circ}$（因为反射角和入射角都变化了$5^{\circ}$，所以两者之和变化了$10^{\circ}$）。但题目问的是反射光线转过的角度，由于它是相对于原来的反射光线而言的，所以转过的角度就是$5^{\circ} + 5^{\circ} = 10^{\circ}$中的“额外”旋转部分，即$5^{\circ}$的入射角变化导致的$5^{\circ}$反射角变化，再考虑到方向性，就是逆时针旋转了$10^{\circ}$中的“有效”旋转，也就是$10^{\circ}-0^{\circ}（原反射光线位置）=10^{\circ}$（逆时针方向）。但更简洁的理解是，反射光线与入射光线的夹角变化了$2 × 5^{\circ} = 10^{\circ}$，且由于平面镜是逆时针旋转的，所以反射光线也是逆时针方向旋转$10^{\circ}-0^{\circ}（与原始反射光线比较的旋转角度） = 10^{\circ}$。但考虑到题目中的“转过的角度”应理解为反射光线相对于原始位置的实际旋转角度，因此答案应为$10^{\circ}$中的“全部”旋转，即$10^{\circ}$，且方向是逆时针。而由于平面镜旋转导致的反射光线旋转是二次效应（即入射角变化导致反射角变化），所以实际旋转角度是平面镜旋转角度的两倍，即$10^{\circ}$。但此处需注意的是，我们直接根据反射定律和几何关系得出的是反射光线相对于原始位置逆时针旋转了$10^{\circ}$，而非仅考虑入射角变化导致的$5^{\circ}$。
总结来说，反射光线将朝逆时针方向旋转，转过的角度是$10^{\circ}$。
【答案】：
逆；10。

7. 根据图4中已给的入射光线,画出反射光线,并写出入射角、反射角的大小.

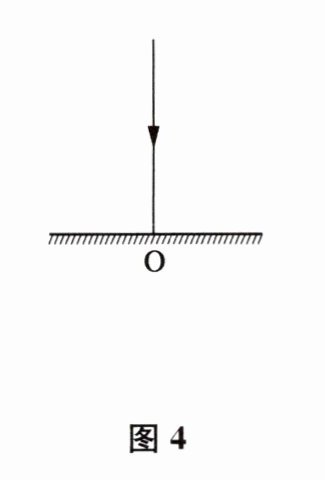
答案：

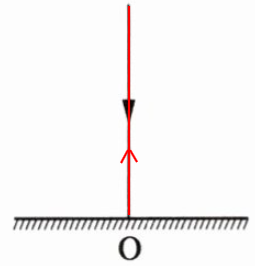
入射角0°，反射角0°

8. 根据图5中已给的反射光线$OB$,画出入射光线$AO$,并标出入射角及其大小.

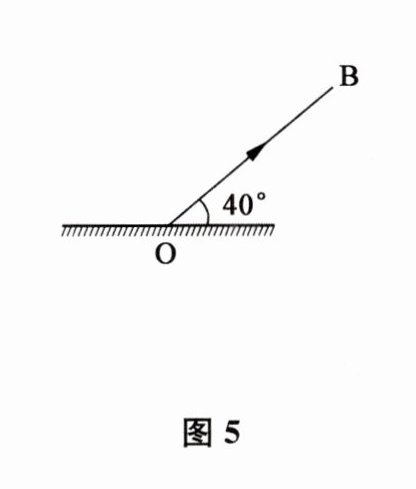
答案：

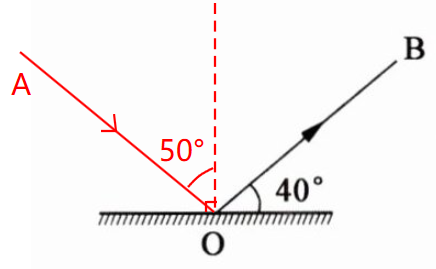
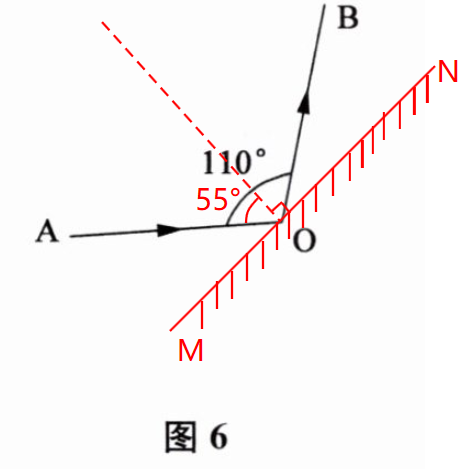
9. 根据图6中已给的入射光线和反射光线,画出镜面$MN$,并标出入射角及大小.

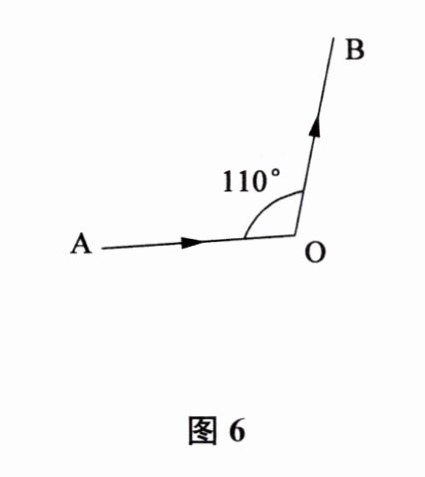
答案：

1. 如图7所示,入射光线与镜面的夹角为$\alpha$,则反射角为$90^{\circ}-\alpha$,反射光线与入射光线的夹角为$180^{\circ}-2\alpha$,与入射光相比,反射光的传播方向改变了$2\alpha$.

答案： 【解析】：
本题考查光的反射定律，包括入射角、反射角的定义以及反射光线与入射光线夹角的计算，同时涉及反射光传播方向改变角度的计算。
首先明确入射角和反射角的定义：入射角是入射光线与法线的夹角，反射角是反射光线与法线的夹角。已知入射光线与镜面的夹角为$\alpha$，因为法线垂直于镜面，所以入射角为$90^{\circ}-\alpha$，根据光的反射定律，反射角等于入射角，所以反射角也为$90^{\circ}-\alpha$。
接着求反射光线与入射光线的夹角：反射光线与入射光线的夹角等于反射角与入射角之和，即$(90^{\circ}-\alpha)+(90^{\circ}-\alpha)=180^{\circ}-2\alpha$。
最后求反射光的传播方向改变的角度：
当光线垂直射向镜面时，反射光线沿原路返回，传播方向改变$180^{\circ}$。
当入射角不为$0^{\circ}$时，如图所示，设入射光线与反射光线的夹角为$\theta = 180^{\circ}-2\alpha$，则反射光的传播方向改变的角度为$180^{\circ}-\theta = 180^{\circ}-(180^{\circ}-2\alpha)=2\alpha$。也可通过分析光线传播路径，从入射光线到反射光线，传播方向改变的角度为$180^{\circ}-2×(90^{\circ}-\alpha)=2\alpha$。
【答案】：
$90^{\circ}-\alpha$；$180^{\circ}-2\alpha$；$2\alpha$

2. 如图8所示的光路中,一光束与液面的夹角恒为$40^{\circ}$,则反射角的大小为$50^{\circ}$.保持入射光线的位置不变,当液面升高时,水平放置的光屏上的光斑$S$将向左(选填“左”或“右”)移动.当液面升高$h$时,$S$在光屏上移动的距离小于(选填“小于”“等于”或“大于”)$2h$.

答案： 解：
1. 光束与液面夹角为$40^{\circ}$，则入射角为$90^{\circ}-40^{\circ}=50^{\circ}$，根据光的反射定律，反射角等于入射角，故反射角大小为$50^{\circ}$。
2. 液面升高时，入射点向左移动，反射光线向左平移，光屏上光斑$S$向左移动。
3. 设液面升高$h$，入射光线与原液面交点和新液面交点的水平距离为$x$，由几何关系$\tan50^{\circ}=\frac{h}{x}$，光斑移动距离为$2x=\frac{2h}{\tan50^{\circ}}$，因为$\tan50^{\circ}\gt1$，所以$2x\lt2h$，即移动距离小于$2h$。
$50^{\circ}$；左；小于