《2025年中学生世界八年级物理第一学期沪教版54制》

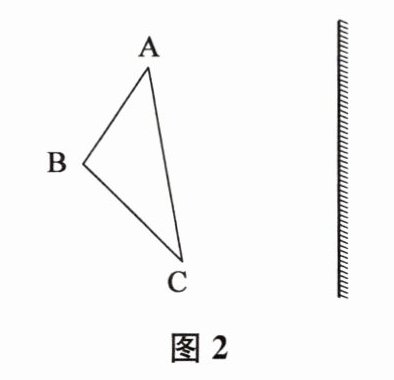
9. 在图2中画出物体ABC在平面镜中所成的像.

答案： 【解析】：
本题主要考查平面镜成像的特点和作图方法。平面镜成像的特点是像与物关于镜面对称，即像与物的大小相等，像与物到镜面的距离相等，且像与物的连线与镜面垂直。根据这些特点，我们可以使用几何作图的方法来画出物体在平面镜中的像。
具体步骤包括：1、确定物体上的关键点（如A、B、C三点）；2、使用对称性质，找出这些关键点关于镜面的对称点（如A'、B'、C'）；3、连接这些对称点，得到物体在平面镜中的像。
【答案】：
图略（由于无法直接绘制图形，这里用文字描述作图步骤）
1、在纸上画出平面镜，并标出物体ABC的位置。
2、分别过A、B、C三点向平面镜作垂线，并延长至镜面后等距的位置，标出对称点A'、B'、C'。
3、连接A'、B'、C'三点，得到物体ABC在平面镜中的像A'B'C'。
注意，像A'B'C'应与物体ABC关于镜面对称，且大小相等。

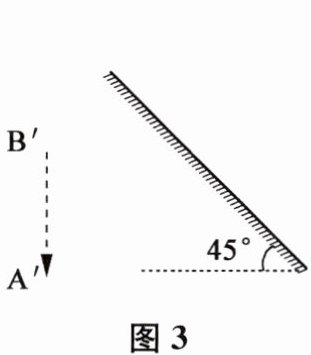
10. 根据平面镜中所成的像A'B',请在图3中利用平面镜成像特点画出物体AB.

答案： 【解析】：
本题考查平面镜成像特点，即像与物关于平面镜对称，像与物的连线与平面镜垂直，像与物到平面镜的距离相等。我们可以利用这些特点，通过作像点$A'$、$B'$关于平面镜的对称点来确定物体$AB$的位置。
1. 首先，过$A'$点向平面镜作垂线，并延长至$A$点，使$A$到平面镜的距离等于$A'$到平面镜的距离。
2. 然后，过$B'$点向平面镜作垂线，并延长至$B$点，使$B$到平面镜的距离等于$B'$到平面镜的距离。
3. 最后，连接$A$、$B$两点，得到物体$AB$。
【答案】：
1. 过$A'$点作平面镜的垂线，延长至$A$，使$A$到平面镜的距离等于$A'$到平面镜的距离。
2. 过$B'$点作平面镜的垂线，延长至$B$，使$B$到平面镜的距离等于$B'$到平面镜的距离。
3. 连接$A$、$B$两点，得到物体$AB$。
图略

实验目的：探究平面镜成像的特点.
实验器材：玻璃板、两支完全相同的蜡烛、刻度尺、白纸等.
实验步骤：1. 在水平桌面上铺一张白纸,纸上竖直放置一块玻璃板作为平面镜.
2. 在玻璃板前放一支点燃的蜡烛A,如图4所示,移动蜡烛B,直到它与镜中的像完全重合,这是为了确定像的位置并比较像与物的大小关系.
……

答案： 实验器材：完全相同
实验步骤：1. 竖直
2. B；确定像的位置并比较像与物的大小关系

如图5所示,墙上挂着长0.6m的平面镜,小明站在镜子前1.2m处,这时他恰好可以通过平面镜看到身后一根木杆完整的像.若木杆高2.4m,则这根木杆和小明的距离是 (B)
A.1.8m
B.2.4m
C.3.0m
D.3.6m

答案： 解：根据平面镜成像特点，像与物到镜面距离相等，设木杆到镜面距离为$d$，则木杆像到镜面距离也为$d$。小明到镜面距离$1.2m$，小明到木杆像的距离为$d + 1.2m$。
由光的反射定律及相似三角形知识（小明眼睛、镜面上下边缘、木杆像上下端构成相似三角形）：
$\frac{平面镜高度}{木杆像高度}=\frac{小明到镜面距离}{小明到木杆像距离}$
$\frac{0.6m}{2.4m}=\frac{1.2m}{d + 1.2m}$
解得$d = 3.6m$
木杆和小明的距离：$d - 1.2m=3.6m - 1.2m=2.4m$
答案：B