第52页
- 第1页
- 第2页
- 第3页
- 第4页
- 第5页
- 第6页
- 第7页
- 第8页
- 第9页
- 第10页
- 第11页
- 第12页
- 第13页
- 第14页
- 第15页
- 第16页
- 第17页
- 第18页
- 第19页
- 第20页
- 第21页
- 第22页
- 第23页
- 第24页
- 第25页
- 第26页
- 第27页
- 第28页
- 第29页
- 第30页
- 第31页
- 第32页
- 第33页
- 第34页
- 第35页
- 第36页
- 第37页
- 第38页
- 第39页
- 第40页
- 第41页
- 第42页
- 第43页
- 第44页
- 第45页
- 第46页
- 第47页
- 第48页
- 第49页
- 第50页
- 第51页
- 第52页
- 第53页
- 第54页
- 第55页
- 第56页
- 第57页
- 第58页
- 第59页
- 第60页
- 第61页
- 第62页
- 第63页
- 第64页
- 第65页
- 第66页
- 第67页
- 第68页
- 第69页
- 第70页
- 第71页
例1 下面能围成正方体的图形是(
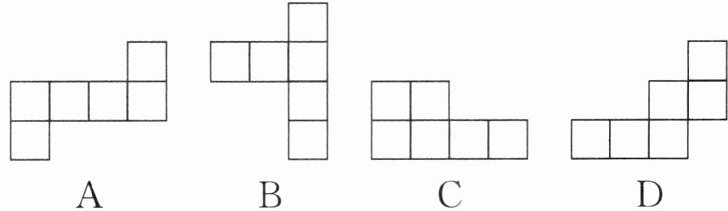
【分析】 看图分析,能围成正方体的图形必须是围成正方体后两两相对的6个小正方形,分析可知,A中的图形符合要求,B,C,D不能围成正方体。
【解答】 A
A
)。
【分析】 看图分析,能围成正方体的图形必须是围成正方体后两两相对的6个小正方形,分析可知,A中的图形符合要求,B,C,D不能围成正方体。
【解答】 A
答案:
解析:
题目考查正方体的展开图。
正方体的展开图有“1-4-1”型、“2-3-1”型、“2-2-2”型、“3-3”型,且展开图中不会出现“凹”和“田”字型。
A选项符合“1-4-1”型,可以围成正方体;
B选项出现“田”字型,不能围成正方体;
C选项和D选项不符合上述几种类型,不能围成正方体。
答案:A。
题目考查正方体的展开图。
正方体的展开图有“1-4-1”型、“2-3-1”型、“2-2-2”型、“3-3”型,且展开图中不会出现“凹”和“田”字型。
A选项符合“1-4-1”型,可以围成正方体;
B选项出现“田”字型,不能围成正方体;
C选项和D选项不符合上述几种类型,不能围成正方体。
答案:A。
例2 右图是一块长方体木块。请按要求答题:
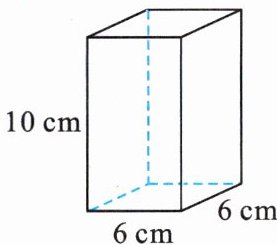
(1)把这块木块放在地面上,占地面积是多少平方厘米?
(2)把这块木块的6个面刷一层油漆,刷漆面积是多少平方厘米?
(3)这块木块的体积是多少立方厘米?
(4)在这块木块中截取一个最大的圆柱,这个圆柱的体积是多少立方厘米?
(5)在这块木块中截取一个最大的圆锥,这个圆锥的体积是多少立方厘米?
【解答】(1)$6× 6= 36$(平方厘米)或$6× 10= 60$(平方厘米)
(2)$6× 6× 2+6× 10× 4= 312$(平方厘米)
(3)$6× 6× 10= 360$(立方厘米)
(4)$3.14× (6÷ 2)^{2}× 10= 282.6$(立方厘米)
(5)$3.14× (6÷ 2)^{2}× 10× \frac{1}{3}= 94.2$(立方厘米)

(1)把这块木块放在地面上,占地面积是多少平方厘米?
(2)把这块木块的6个面刷一层油漆,刷漆面积是多少平方厘米?
(3)这块木块的体积是多少立方厘米?
(4)在这块木块中截取一个最大的圆柱,这个圆柱的体积是多少立方厘米?
(5)在这块木块中截取一个最大的圆锥,这个圆锥的体积是多少立方厘米?
【解答】(1)$6× 6= 36$(平方厘米)或$6× 10= 60$(平方厘米)
(2)$6× 6× 2+6× 10× 4= 312$(平方厘米)
(3)$6× 6× 10= 360$(立方厘米)
(4)$3.14× (6÷ 2)^{2}× 10= 282.6$(立方厘米)
(5)$3.14× (6÷ 2)^{2}× 10× \frac{1}{3}= 94.2$(立方厘米)
答案:
(1)占地面积有两种可能:
底面为$6×6$的面:
$6 × 6 = 36 \text{平方厘米}$;
底面为$6×10$的面:
$6 × 10 = 60 \text{平方厘米}$。
(2)长方体的表面积公式为$2(ab + ah + bh)$,其中$a$、$b$、$h$分别为长方体的长、宽、高:
$2×(6 × 6 + 6 × 10 + 6 × 10) $
$= 2 × (36 + 60 + 60) $
$= 2 × 156 $
$= 312 \text{平方厘米}$
(3)长方体的体积公式为$V = abh$:
$6 × 6 × 10 = 360 \text{立方厘米}$。
(4)圆柱的底面直径为$6$厘米,高为$10$厘米,圆柱体积公式为$V = \pi r^2 h$,其中$r$为半径,$h$为高:
$r = \frac{6}{2} = 3 \text{厘米}$,
$V = 3.14 × 3^2 × 10 = 3.14 × 9 × 10 = 282.6 \text{立方厘米}$。
(5)圆锥的底面直径为$6$厘米,高为$10$厘米,圆锥体积公式为$V = \frac{1}{3} \pi r^2 h$:
$r = \frac{6}{2} = 3 \text{厘米}$,
$V = \frac{1}{3} × 3.14 × 3^2 × 10 = \frac{1}{3} × 3.14 × 9 × 10 = 94.2 \text{立方厘米}$。
(1)占地面积有两种可能:
底面为$6×6$的面:
$6 × 6 = 36 \text{平方厘米}$;
底面为$6×10$的面:
$6 × 10 = 60 \text{平方厘米}$。
(2)长方体的表面积公式为$2(ab + ah + bh)$,其中$a$、$b$、$h$分别为长方体的长、宽、高:
$2×(6 × 6 + 6 × 10 + 6 × 10) $
$= 2 × (36 + 60 + 60) $
$= 2 × 156 $
$= 312 \text{平方厘米}$
(3)长方体的体积公式为$V = abh$:
$6 × 6 × 10 = 360 \text{立方厘米}$。
(4)圆柱的底面直径为$6$厘米,高为$10$厘米,圆柱体积公式为$V = \pi r^2 h$,其中$r$为半径,$h$为高:
$r = \frac{6}{2} = 3 \text{厘米}$,
$V = 3.14 × 3^2 × 10 = 3.14 × 9 × 10 = 282.6 \text{立方厘米}$。
(5)圆锥的底面直径为$6$厘米,高为$10$厘米,圆锥体积公式为$V = \frac{1}{3} \pi r^2 h$:
$r = \frac{6}{2} = 3 \text{厘米}$,
$V = \frac{1}{3} × 3.14 × 3^2 × 10 = \frac{1}{3} × 3.14 × 9 × 10 = 94.2 \text{立方厘米}$。
查看更多完整答案,请扫码查看


