《2025年小学升初中衔接读本数学》

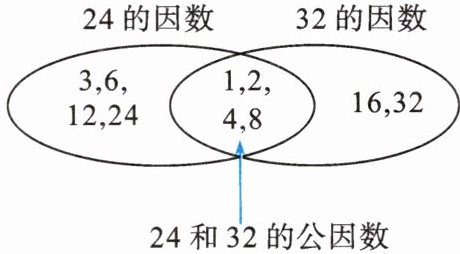
例2 在圈里填上适当的数。

【分析】 24的因数有1,2,3,4,6,8,12,24;32的因数有1,2,4,8,16,32;24和32的公因数有1,2,4,8。
【解答】

答案： 本题可根据因数和公因数的定义，结合所给示例进行解答。
分析
因数是指整数$a$除以整数$b(b\neq0)$ 的商正好是整数而没有余数，此时称$b$是$a$的因数。
公因数是指一个能被若干个整数同时均整除的整数。如果一个整数同时是几个整数的因数，称这个整数为它们的“公因数”。
解答
步骤一：找出$24$的因数
根据因数的定义，$24÷1 = 24$，$24÷2 = 12$，$24÷3 = 8$，$24÷4 = 6$，$24÷6 = 4$，$24÷8 = 3$，$24÷12 = 2$，$24÷24 = 1$，所以$24$的因数有$1, 2, 3, 4, 6, 8, 12, 24$。
步骤二：找出$32$的因数
同理，$32÷1 = 32$，$32÷2 = 16$，$32÷4 = 8$，$32÷8 = 4$，$32÷16 = 2$，$32÷32 = 1$，所以$32$的因数有$1, 2, 4, 8, 16, 32$。
步骤三：找出$24$和$32$的公因数
对比$24$和$32$的因数，可得它们公有的因数，即公因数为$1, 2, 4, 8$。
在图中，左边圈里填$24$的因数中除公因数外的数，即$3, 6, 12, 24$；右边圈里填$32$的因数中除公因数外的数，即$16, 32$；中间相交部分填$24$和$32$的公因数$1, 2, 4, 8$。
故答案为：左边圈：$3, 6, 12, 24$；中间相交圈：$1, 2, 4, 8$；右边圈：$16, 32$。

例3 有一张长为120厘米,宽为80厘米的长方形纸片裁成同样大小的正方形纸片,且无剩余,至少能裁多少张？
【分析】 本题的关键是找出正方形的边长。要正好裁成同样大小的正方形,则正方形的边长应该是120和80的公因数。要使正方形尽可能大,则边长尽量大,即取120和80的最大公因数,所以正方形的边长是40厘米。
【解答】 $120÷40 = 3$(个) $80÷40 = 2$(个)
$3×2 = 6$(个)

答案： 【分析】
本题主要考查最大公因数的应用。
为了使得裁剪出的正方形数量最少，正方形的边长应该是长和宽的最大公因数。
因此，我们需要找到120和80的最大公因数，用这个最大公因数作为正方形的边长，然后分别计算长和宽能裁出多少个这样的正方形，最后相乘即得到正方形的数量。
【解答】
解：首先求120和80的最大公因数。
120和80的最大公因数为40，所以正方形的边长为40厘米。
$120 ÷ 40 = 3$（个）
$80 ÷ 40 = 2$（个）
所以能裁出正方形的数量为：
$3 × 2 = 6$（个）
答：至少能裁6张。

例 用提取公因式的方法分解因式。
$24abc - 9ab$ $ab + bc$ $3x^{2}+x$
【分析】 一般,如果多项式的各项有公因式,可以把这个公因式提到括号外面,将多项式写成因式相乘的形式,这种分解因式的方法叫作提公因式法。
【解答】 $24abc - 9ab= 3ab(8c - 3)$
$ab + bc = b(a + c)$
$3x^{2}+x= x(3x + 1)$

答案： 【分析】
题目要求使用提取公因式的方法分解因式。提取公因式是一种基本的代数技能，需要找到多项式各项中的公共因子，并将其提取出来，从而将多项式简化为几个因式的乘积。
【解答】
对于 $24abc - 9ab$，可以观察到公因式为 $3ab$，提取公因式后得到：
$24abc - 9ab = 3ab(8c - 3)$
对于 $ab + bc$，公因式是 $b$，提取后得到：
$ab + bc = b(a + c)$
对于 $3x^{2} + x$，公因式是 $x$，提取后得到：
$3x^{2} + x = x(3x + 1)$

一、判断。(对的画“√”,错的画“×”)
1. 因为$7×8 = 56$,所以56是倍数,7和8是因数。(×)
2. 一个数的因数都比这个数的倍数小。(×)
3. $n$是奇数,$3n + 1$一定是偶数。(√)
4. 一个合数至少有3个因数。(√)
5. 所有的奇数都是质数,所有的偶数都是合数。(×)
6. 两个数的最小公倍数一定比这两个数大。(×)
7. 4的倍数比40的倍数少。(×)
8. 在既是合数又是奇数的自然数中,最小的是9。(√)
9. $1 + 2 + 3+…+2018$的和是奇数。(√)
10. 一个数的质因数都是质数。(√)

答案： 1. × 2. × 3. √ 4. √ 5. × 6. × 7. × 8. √ 9. √ 10. √