《2025年暑假生活江苏人民出版社八年级数学》

20. 解下列分式方程：
(1)$\frac {3}{x-1}= \frac {2}{x+1}$；
(2)$\frac {x+1}{x-1}-\frac {2}{x^{2}-1}= \frac {1}{x+1}$.

答案：
(1)方程两边同乘$(x - 1)(x + 1)$，得$3(x + 1)=2(x - 1)$，展开得$3x + 3=2x - 2$，移项得$3x - 2x=-2 - 3$，解得$x=-5$，检验：当$x=-5$时，$(x - 1)(x + 1)=(-5 - 1)(-5 + 1)=(-6)(-4)=24\neq0$，所以$x=-5$是原方程的解。
(2)方程两边同乘$(x - 1)(x + 1)$，得$(x + 1)^2 - 2=x - 1$，展开得$x^2 + 2x + 1 - 2=x - 1$，化简得$x^2 + 2x - 1=x - 1$，移项得$x^2 + 2x - x - 1 + 1=0$，即$x^2 + x=0$，因式分解得$x(x + 1)=0$，解得$x=0$或$x=-1$，检验：当$x=-1$时，$(x - 1)(x + 1)=0$，所以$x=-1$是增根；当$x=0$时，$(x - 1)(x + 1)=(-1)(1)=-1\neq0$，所以原方程的解为$x=0$。

21. 一个不透明的袋中装有 20 个只有颜色不同、其他完全相同的球,其中 5 个黄球,8 个黑球,7 个红球.
(1)求从袋中摸出一个球是黄球的概率；
(2)现从袋中取出若干个黑球,搅匀后,使从袋中摸出一个球是黑球的概率是$\frac {1}{3}$,求从袋中取出黑球的个数.

答案：
(1) 袋中共有20个球，其中黄球5个，摸出一个球是黄球的概率为：$\frac{5}{20}=\frac{1}{4}$。
(2) 设取出黑球的个数为$x$，则剩余黑球为$(8 - x)$个，总球数为$(20 - x)$个。由题意得：$\frac{8 - x}{20 - x}=\frac{1}{3}$，解得$x = 2$。即从袋中取出黑球的个数为2个。

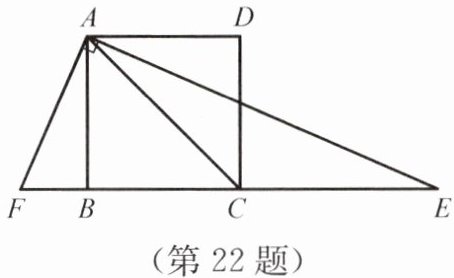
22. 如图所示,正方形 ABCD 的边长为 3,连接 AC,AE 平分$∠CAD$,交 BC 的延长线于点 E,$FA⊥AE$交 CB 的延长线于点 F,求 EF 的长.

答案： 解：
∵ 四边形ABCD为正方形，且边长为3，
∴ AC=3√2.
∵ AE平分∠CAD，
∴ ∠CAE=∠DAE.
∵ AD // CE，
∴ ∠DAE=∠E，
∴ ∠CAE=∠E，
∴ CE=CA=3√2.
∵ FA⊥AE，
∴ ∠FAC+∠CAE=90°，∠F+∠E=90°.
∴ ∠FAC=∠F.
∴ CF=AC=3√2.
∴ EF=CF+CE=3√2+3√2=6√2.

23. 某商场购进甲、乙两种商品,乙商品的单价是甲商品单价的 2 倍,购买 240 元甲商品的数量比购买 300 元乙商品的数量多 15 件,求两种商品单价各为多少元.

答案： 解：设甲商品的单价为x元，则乙商品的单价为2x元. 根据题意，得240/x - 300/(2x)=15.
∴ x=6.
∴ 2x=2×6=12. 答：甲、乙商品的单价分别为6元、12元.